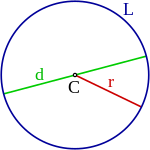
Círculo
|
Read other articles:

Épinay-sur-SeineNegaraPrancisArondisemenSaint-DenisAntarkomuneCommunautéd'agglomérationPlaine CommuneKode INSEE/pos93031 / Épinay-sur-Seine merupakan sebuah komune di pinggiran utara Paris, Prancis. Terletak 11.3 km (7 mil) dari pusat kota Paris. Gereja Notre-Dame-des-Missions-du-cygne d'Enghien, dirancang Paul Tournon, dapat ditemukan di komune ini. Sejarah Tanggal 7 Agustus 1850, sebagian teritori Épinay-sur-Seine dipisahkan dan bergabung dengan teritori Deuil-la-Barre, Sain...

Umberto Colombo Colombo alla Juventus nella stagione 1957-58 Nazionalità Italia Altezza 183 cm Peso 77 kg Calcio Ruolo Centrocampista Termine carriera 1967 Carriera Giovanili 19??-19?? Juventus Squadre di club1 1951-1952 Juventus0 (0)1952-1954→ Monza48 (10)1954-1961 Juventus173 (22)1961-1966 Atalanta142 (3)1966-1967 Verona4 (0) Nazionale 1959-1960 Italia3 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il si...

Lebanese Broadcasting Corporation InternationalLogo LBC International NewsDiluncurkan23 Agustus 1985 (jaringan televisi)PemilikGrup pebisnis LebanonSloganEl Dunia Alwan (Arab: الدنيا ألوانcode: ar is deprecated )NegaraLebanonSitus webwww.lbci.com Lebanese Broadcasting Corporation International (Arab: المؤسسة اللبنانية للإرسال انترناسيونالcode: ar is deprecated ), dikenal luas sebagai LBCI, adalah sebuah stasiun televisi swasta di Lebanon. LBCI did...

#thatPowerSingel oleh will.i.am featuring Justin Bieberdari album #willpowerDirilis18 Maret 2013Direkam20 Februari 2013GenreDance-pop[1]Durasi4:39Label will.i.am Music Interscope Pencipta William Adams Damien LeRoy Justin Bieber Produser will.i.am Verrigni Damien Leroy Kronologi singel will.i.am Scream & Shout (2012) #thatPower (2013) Crazy Kids (2013) Kronologi singel Justin Bieber All Around the World(2013) #thatPower(2013) Lolly(2013) Video musik#thatPower ft. Justin ...

إكسوكي (إوانينا) تقسيم إداري البلد اليونان [1] إحداثيات 39°41′15″N 20°49′21″E / 39.6875°N 20.8225°E / 39.6875; 20.8225 السكان التعداد السكاني 3302 (resident population of Greece) (2021)2975 (resident population of Greece) (2011) الرمز الجغرافي 10175092 تعديل مصدري - تعديل إكسوكي (Εξοχή) هي مدينة في إوان�...

Cet article est une ébauche concernant le cyclisme. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Grand Prix Slovenian IstriaNoms officiels2014-2018 GP Izoladepuis 2019 GP Slovenian IstriaGénéralitésSport Cyclisme sur routeCréation 2014Nombre d'éditions 10 (en 2024)Périodicité annuelle (mars)Type / Format Course d'un jourLieu(x) SlovénieCatégorie 1.2 (depuis 2014)Circuit UCI Europe TourSite web offic...

Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standar Wikipedia. Mohon tulis paragraf pembuka yang informatif sehingga pembaca dapat memahami maksud dari Daftar penumpang RMS Titanic. Contoh paragraf pembuka Daftar penumpang RMS Titanic adalah .... (Juni 2020) (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Daftar penumpang Kelas satu Nama Allen, Miss Elizabeth Walton Allison, Mr. Hudson Joshua Creighton Mr. George Swane Miss Amelia Mary Mildred Brown Alliso...

Untuk penyanyi dan pemeran, lihat Fang Wen-lin. Untuk penyair Amerika Serikat, lihat Marilyn Chin. Ini adalah nama Tionghoa; marganya adalah Chen. Chen Mei-ling陳美伶 Menteri Dewan Pembangunan Nasional Republik TiongkokMasa jabatan8 September 2017 – 19 Mei 2020WakilChiou Jiunn-rong, Tseng Shu-cheng, Kao Shien-quey PendahuluChen Tain-jyPenggantiKung Ming-hsinSekretaris-Jenderal Yuan EksekutifMasa jabatan20 Mei 2016 – 7 September 2017Perdana MenteriLin ChuanWakilHo Pei-...

Pour les articles homonymes, voir Menez. Menez DreganFouilles en cours.LocalisationCoordonnées 47° 59′ 11″ N, 4° 28′ 31″ OLocalisation Plouhinec FranceLocalité voisine PlouhinecCaractéristiquesType Ancienne grotte marinePériode de formation Paléolithique inférieurLocalisation sur la carte du FinistèreLocalisation sur la carte de Francemodifier - modifier le code - modifier Wikidata Menez Dregan est un site préhistorique de la commune de Pl...

Voroneț redirects here. For the town where the monastery is located, see Gura Humorului. Voroneț MonasteryMonastery informationFull nameVoroneț MonasteryOther namesSistine Chapel of the EastOrderRomanian OrthodoxEstablished1488Dedicated toSaint GeorgePeopleFounder(s)Stephen the Great of MoldaviaArchitectureStyleMoldavianCompletion date14 September 1488SiteLocation6 km (3.7 mi) from Voroneț, Suceava County, RomaniaCoordinates47°31′1.56″N 25°51′51.3″E / 4...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

40°49′37.8″N 73°41′59.2″W / 40.827167°N 73.699778°W / 40.827167; -73.699778 American Aeronautical CorporationIndustryAerospaceFoundedOctober 1928 (1928-10)FounderEnea Bossi Sr.HeadquartersPort Washington, New York, United States Enea Bossi in front of the AAC factory in Port Washington, New York The American Aeronautical Corporation (AAC) was founded in October 1928 by Enea Bossi, located at 730 Fifth Avenue in Port Washington, New York. Its purpo...

This article is about Islamic views on slavery. For other uses, see Islam and slavery (disambiguation). Part of a series onIslam Beliefs Oneness of God Angels Revealed Books Prophets Day of Resurrection Predestination Practices Profession of Faith Prayer Almsgiving Fasting Pilgrimage TextsFoundations Quran Sunnah (Hadith, Sirah) Tafsir (exegesis) Aqidah (creed) Qisas al-Anbiya (Stories of the Prophets) Mathnawi (Poems) Fiqh (jurisprudence) Sharia (law) History Timeline Muhammad Ahl al-Bayt S...
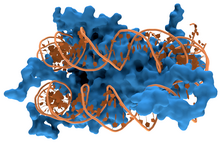
Proteins that bind with DNA, such as transcription factors, polymerases, nucleases and histones Cro protein complex with DNA Interaction of DNA (orange) with histones (blue). These proteins' basic amino acids bind to the acidic phosphate groups on DNA. The lambda repressor helix-turn-helix transcription factor bound to its DNA target[1] The restriction enzyme EcoRV (green) in a complex with its substrate DNA[2] DNA-binding proteins are proteins that have DNA-binding domains an...

العلاقات النيوزيلندية الهندوراسية نيوزيلندا هندوراس نيوزيلندا هندوراس تعديل مصدري - تعديل العلاقات النيوزيلندية الهندوراسية هي العلاقات الثنائية التي تجمع بين نيوزيلندا وهندوراس.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعي...

ألفريد هيراداتيري أمير ساكس كوبورج وغوتا معلومات شخصية الميلاد 15 أكتوبر 1874(1874-10-15)قصر بكنغهام الوفاة 6 فبراير 1899 (24 سنة) ميرانو سبب الوفاة إصابة بعيار ناري مكان الدفن كوبورغ مواطنة القيصرية الألمانية الأب ألفريد دوق ساكس كوبورغ وغوتا الأم الدوقة ...

Hindu temple in Varanasi, Uttar Pradesh, India Kashi Vishwanath redirects here. For other uses, see Kashi Vishwanath (disambiguation). Not to be confused with Shri Vishwanath Temple, BHU. For other uses, see Kashi Vishwanath Temple (disambiguation). Kashi Vishwanath TempleEntrance to present temple built by Ahilyabai Holkar in the 1780.ReligionAffiliationHinduismDistrictVaranasiDeityVishveshwara or Vishwanath (Shiva)FestivalsMaha ShivaratriGoverning bodyShri Kashi Vishwanath Temple TrustLocat...

Shah MosqueMasjed-e ShahImam Mosque (Masjed-e Imam)Masjed-e Jameh AbbasiAgamaAfiliasiShia IslamKepemimpinanMayor of IsfahanStatusActiveLokasiLokasiIsfahan, IranKoordinat32°39′16″N 51°40′39″E / 32.65444°N 51.67750°E / 32.65444; 51.67750ArsitekturArsitekShaykh BahaiGaya arsitekturFour-iwan formatPeletakan batu pertama1611Rampung1629Biaya konstruksi60,000 tomansSpesifikasiPanjang100 mLebar130 mTinggi luar kubah53 mMenara4Tinggi menara42 m Masjid Shah dikenal p...

La ruta del tercer viaje de Cook se muestra en rojo, y en azul la que se siguió después de su muerte. El tercer y último viaje de James Cook (12 de julio de 1776 - 4 de octubre de 1780) tomó la ruta de Plymouth a través de Ciudad del Cabo y Tenerife a Nueva Zelanda y las islas hawaianas, y a lo largo de la costa norteamericana hasta el Estrecho de Bering. Su propósito aparente era devolver a Omai, un joven de Raiatea, a su tierra natal, pero el almirantazgo lo utilizó como tapadera par...

306th Rifle Division (September 1941 – ?)306th Rifle Division (June 16, 1942 – 1945)A copy of the division's banner in a museum in DukhovshchinaActive1941–1945Country Soviet UnionBranch Red ArmyTypeInfantrySizeDivisionEngagementsBattle of SmolenskVitebsk-Orsha OffensiveŠiauliai OffensiveRiga OffensiveCourland PocketDecorations Order of the Red BannerBattle honoursRibshevoCommandersNotablecommandersCol. Stepan Ivanovich ChernyakCol. Georgii Matveevich KostikCol. Vasi...