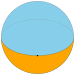
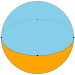
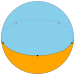
Dihedron
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Pakuwon MallPakuwon Mall saat renovasi dan perluasan (2016)LokasiSurabaya, IndonesiaKoordinat7°17′22.5″S 112°40′30.4″E / 7.289583°S 112.675111°E / -7.289583; 112.675111Koordinat: 7°17′22.5″S 112°40′30.4″E / 7.289583°S 112.675111°E / -7.289583; 112.675111AlamatJalan Puncak Indah Lontar No.2Kelurahan Babatan, Kecamatan WiyungKota Surabaya, Jawa Timur 60227Tanggal dibuka8 November 2003 (Supermal Pakuwon Indah)13 November 200...
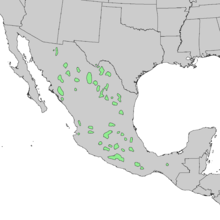
Species of conifer Juniperus flaccida J. flaccida in Big Bend National Park Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Gymnospermae Division: Pinophyta Class: Pinopsida Order: Cupressales Family: Cupressaceae Genus: Juniperus Species: J. flaccida Binomial name Juniperus flaccidaSchltdl. Natural range of Juniperus flaccida Juniperus flaccida (drooping juniper, weeping juniper or Mexican juniper; Nativ...

Untuk orang lain yang juga bernama William Wallace, lihat William Wallace (disambiguasi).Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: William Wallace – berita · surat kabar · buku · cendekiawan · JSTOR Sir William WallaceLahir1272Elderslie or Eller...

Pour les articles homonymes, voir Gobry. Ivan GobryIvan Gobry lors de sa remise de la Légion d'honneur, en 1997.BiographieNaissance 8 mars 1927Saint-André-les-Vergers (Aube, Grand Est, France)Décès 3 août 2017 (à 90 ans)12e arrondissement de Paris (Paris, Île-de-France, France)Nom de naissance Yvan Louis GobryNationalité françaiseFormation Université de ParisActivités Essayiste, écrivain, professeur d'université, historienEnfant Claire FontanaAutres informationsA travaillé...

Artikel ini bukan mengenai Tayu. Tayo the Little BusGenreAnimasi, Anak-anak, KomediDitulis olehChoi Jong-IlSutradaraKim Min-sungPengisi suaraRobyn Slade - TayoNolan Balzer - RogiKami Desilets - LaniKerri Salki - GaniLagu pembukaTayo the Little BusLagu penutupVroom, Vroom, Vroom!Negara asal Korea SelatanBahasa asliKoreaInggris (Dubbed)Indonesia (Dubbed)Jmlh. musim5ProduksiDurasi15 menit per episodeRumah produksiIconix EntertainmentEducational Broadcasting SystemDistributorEducational Broa...

Tanda tempelan beraneka bahasa dalam bahasa Arab, bahasa Ibrani, bahasa Inggris dan bahasa Rusia yang bertempat di kantor Kementerian Dalam Negeri Israel dan Kementerian Penyerapan Penduduk Perantau Israel di kota Haifa. Tanda peringatan beraneka bahasa dalam bahasa Arab, Ibrani, Inggris dan Rusia pada penutup lubang got berserat optik di tempat kedudukan pusat pemerintahan negara Israel, kota Tel Aviv. Papan penunjuk jalan di Israel yang tercantum dalam bahasa Arab, bahasa Ibrani dan bahasa ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Protokol Milwaukee, kadang-kadang disebut Protokol Wisconsin,[1][2] adalah metode eksperimental untuk menangani infeksi rabies pada manusia. Metode ini membuat pasien menjadi koma dengan menggunakan obat-obatan. Pasien yang sudah koma ...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Pour les articles homonymes, voir Churchill. Ne doit pas être confondu avec Randolph Churchill (1911-1968). Pour les autres membres de la famille, voir Famille Spencer. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (août 2020). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les ...

For other uses, see Wadding (disambiguation). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2023) (Learn how and when to remove this template message) Wadding is a disc of material used in guns to seal gas behind a projectile (a bullet or ball), or to separate the propellant from loosely packed shots.[1] Wadding can be crucial to a gun's effic...

Term used to critique certain forms of feminist activism Part of a series onFeminism History Feminist history History of feminism Women's history American British Canadian German Waves First Second Third Fourth Timelines Women's suffrage Muslim countries US Other women's rights Women's suffrage by country Austria Australia Canada Colombia India Japan Kuwait Liechtenstein New Zealand Spain Second Republic Francoist Switzerland United Kingdom Cayman Islands Wales United States states Intersecti...

American singer (born 1971) This article is about the lead singer of Korn. For people with similar names, see Jonathan Davis (disambiguation). Jonathan DavisDavis performing with Korn in 2018Background informationBirth nameJonathan Howsmon DavisAlso known as JD JDevil J Devil Born (1971-01-18) January 18, 1971 (age 53)Bakersfield, California, U.S.Genres Nu metal alternative metal industrial metal electronica alternative rock Occupation(s) Singer songwriter musician producer Instrument(s)...

Torneo di Wimbledon 1932Doppio femminile Sport Tennis Vincitrici Doris Metaxa Josane Sigart Finaliste Elizabeth Ryan Helen Jacobs Punteggio 6-4, 6-3 Tornei Singolare uomini donne Doppio uomini donne misto 1931 1933 Voce principale: Torneo di Wimbledon 1932. Doris Metaxa e Josane Sigart hanno sconfitto in finale Elizabeth Ryan e Helen Jacobs col punteggio di 6-4, 6-3. Indice 1 Teste di serie 2 Tabellone 2.1 Legenda 2.2 Fase finale 2.3 Parte alta 2.3.1 Sezione 1 2.3.2 Sezione 2 2.4 Part...

Karl RadekKarl Radek sekitar 1919LahirKarol Sobelsohn(1885-10-31)31 Oktober 1885Lemberg, Austria-Hungaria (sekarang Lviv, Ukraina)Meninggal19 Mei 1939(1939-05-19) (umur 53)Verkhneuralsk, RSFS Rusia, Uni Soviet(sekarang Federasi Rusia)KebangsaanPolandiaNama lainKarl Berngardovich RadekWarga negaraKekaisaran Rusia, Uni SovietPekerjaanRevolusioner, penulis, jurnalis, wartawan, politisi, teoretikusTahun aktif1904–1939OrganisasiKomunis InternasionalDikenal atasAktivisme revolusio...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Japanese light novel series Asura Cryin'Cover of the first light novel cover featuring Misao Minakami.アスラクライン(Asura Kurain)GenreAction, supernatural[1] Light novelWritten byGakuto MikumoIllustrated byNao WatanukiPublished byASCII Media WorksImprintDengeki BunkoDemographicMaleOriginal runJuly 10, 2005 – February 10, 2010Volumes14 MangaWritten byGakuto MikumoIllustrated byRyō AkizukiPublished byASCII Media WorksMagazineDengeki DaiohDemograp...

Robert Almer Almer dengan Austria Wien pada tahun 2009.Informasi pribadiTanggal lahir 20 Maret 1984 (umur 40)Tempat lahir Bruck an der Mur, AustriaTinggi 1,94 m (6 ft 4+1⁄2 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini Austria WienNomor 1Karier junior SC UntersiebenbrunnKarier senior*Tahun Tim Tampil (Gol)2002–2003 SC Untersiebenbrunn 10 (0)2004–2005 DSV Leoben 14 (0)2005–2006 FK Austria Wien Amateure 7 (0)2006–2008 SV Mattersburg 20 (0)2008–...

Provinsi Tango (丹後国code: ja is deprecated , tango no kuni) adalah provinsi lama Jepang dengan wilayah yang berhadapan dengan Laut Jepang dan sekarang menjadi bagian utara prefektur Kyoto. Tango berbatasan dengan provinsi Tajima, Tamba dan Wakasa. Ibu kota berpindah-pindah di antara kedua kota besar di provinsi Tango, Maizuru dan Miyazu. lbsProvinsi lama Jepang Aki Awa (Kanto) Awa (Shikoku) Awaji Bingo Bitchu Bizen Bungo Buzen Chikugo Chikuzen Chishima Dewa Echigo Echizen Etchu Harima H...