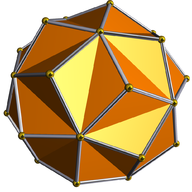
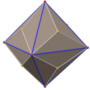
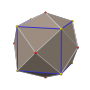
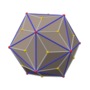
Triakis icosahedron
| |||||||||||||||||||||||||
Read other articles:

Netralitas artikel ini dipertanyakan. Diskusi terkait dapat dibaca pada the halaman pembicaraan. Jangan hapus pesan ini sampai kondisi untuk melakukannya terpenuhi. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Mahendra Bir Bikram ShahRaja NepalRaja NepalBerkuasa13 Maret 1955 – 31 Januari 1972PendahuluTribhuvanPenerusBirendraInformasi pribadiWangsaDinasti ShahAnakBirendra, Gyanendra, Dhirendra Mahendra Bir Bikram Shah, Raja Nepal (11 Juni 1920 – 31 Janu...

Sekolah Menengah Atas Trinitas BandungInformasiDidirikan1 Agustus 1963 dengan nama SMA TRINITASJenisSwastaAkreditasiAKepala SekolahSuro Mulyono, S.Pd., M.Kom.Jumlah kelas7 kelas setiap tingkatJurusan atau peminatanIPA, dan IPSRentang kelasX, XI IPA, XI IPS, XII IPA, XII IPSKurikulumKurikulum 2013, Kurikulum MerdekaAlamatLokasiJalan Kebonjati 209, Bandung, Jawa Barat, IndonesiaTel./Faks.(022)-6019854Koordinat-6.915692514466301, 107.5916697Situs websmatrinitas.sch.idMotoMot...

Gereja Santo YosefAgamaAfiliasiGereja Katolik RomaDistrikCentral RegionLokasiLokasi143 Victoria Street SingapuraArsitekturGaya arsitekturKebangkitan GotikPeletakan batu pertama1904 (bangunan saat ini)Rampung1912 (bangunan saat ini)SpesifikasiPanjang66,25 mLebar45 mLebar tengah18,75mSitus webhttp://www.catholic.org.sg/sjc/index.html Gereja Santo Yosef adalah sebuah gereja Katolik di Singapura. Gereja ini terletak di sepanjang Victoria Street di Rochor Planning Area, dalam Central Area di...

كأس إسكتلندا 1951–52 تفاصيل الموسم كأس إسكتلندا النسخة 67 البلد المملكة المتحدة التاريخ بداية:26 يناير 1952[1] نهاية:19 أبريل 1952[1] المنظم الاتحاد الإسكتلندي لكرة القدم البطل نادي ماذرويل كأس إسكتلندا 1950–51 كأس إسكتلندا 1952–53 تعديل مصدري - تعدي...

Cet article est une ébauche concernant la politique française. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Ministère de la Cohésion des territoiresLe ministre, Christophe Béchu, depuis 2022CadreType Ministère, fonction publique, page de liste de WikimédiaForme juridique MinistèreDomaine d'activité Administration publique généraleSiège Hôtel de CastriesPays FranceLangue FrançaisOrganisatio...

Asosiasi Sepak Bola PolandiaUEFADidirikan1919Kantor pusatWarsawaBergabung dengan FIFA1923Bergabung dengan UEFA1955PresidenZbigniew BoniekWebsitewww.pzpn.pl Asosiasi Sepak Bola Polandia (bahasa Polandia: Polski Związek Piłki Nożnej (PZPN)) adalah badan pengendali sepak bola di Polandia. Kompetisi Badan ini menyelenggarakan beberapa kompetisi di Polandia, yakni: Ekstraklasa Liga Divisi Satu Polandia Liga Divisi Dua Polandia Liga Divisi Tiga Polandia Piala Polandia Piala Liga Polandia Pia...

Norwegian-Finnish aerospace and defence company Nammo ASCompany typePrivateIndustryDefense industryAerospace industryFounded1998; 26 years ago (1998)HeadquartersRaufoss, NorwayKey peopleMorten Brandtzæg (CEO)ProductsAmmunition, missiles, explosives, rocket engines, and propulsion systemsRevenueNOK 7.45 billion (2022)[1]Number of employees2800 (2022)[1]ParentNorwegian Ministry of Trade and Industry (50%)Patria 50% (50.1% owned by the government of Finland and...

此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

2004 studio album by VaderThe BeastCover art by Jacek WiśniewskiStudio album by VaderReleased8 September 2004RecordedRG Studio, Gdańsk, May–June 2004[1]GenreDeath metalLength37:48LabelMetal Mind, Metal BladeProducerPiotr WiwczarekVader chronology Blood(2003) The Beast(2004) The Art of War(2005) Singles from The Beast Beware the BeastReleased: 24 August 2004 Professional ratingsReview scoresSourceRatingChronicles of Chaos[2]Teraz Rock[3]Exclaim!favorable ...

1999 studio album by OrbitalThe Middle of NowhereStudio album by OrbitalReleased5 April 1999Recorded1997–1998GenreTechno, house, ambient technoLength63:59LabelFFRRLondon/Sire Records (US)ProducerOrbitalOrbital chronology In Sides(1996) The Middle of Nowhere(1999) The Altogether(2001) Singles from The Middle of Nowhere StyleReleased: 8 March 1999 Nothing LeftReleased: 5 July 1999 The Middle of Nowhere is the fifth album released by Orbital. It was released in 1999, where it peaked a...

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国(中部イタリア)スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世(スポレート公)、母アルダその他のヨハネステンプレートを表示 ヨハネス12世(Ioannes XII、937年 - 964年5月14日)は、ロ...

Greek table tennis player Panagiotis GionisGionis in 2016Personal informationFull namePanagiotis GionisNickname(s)Gio, The DefentistNationality GreeceBorn (1980-01-07) 7 January 1980 (age 44)Athens, GreeceHeight1.88 m (6 ft 2 in)Weight85 kg (187 lb)Table tennis career Playing styleShakehandEquipment(s)Butterfly Petr Korbel FL blade; Butterfly Tenergy 05 Hard (Black, FH); Butterfly Feint Long II (Red, BH) [1]Highest ranking18 (November 2014)...

3548 EurybatesCiri-ciri orbitAphelion5.650Perihelion4.711Sumbu semimayor5.181Eksentrisitas0.091Anomali rata-rata103.87Inklinasi8.1Bujur node menaik43.6Argumen perihelion27.7Ciri-ciri fisikMagnitudo mutlak (H)9.7 3548 Eurybates (1973 SO) adalah sebuah asteroid. Asteroid ini merupakan bagian dari asteroid Troya Yupiter, yang terletak di orbit Yupiter. Eksentrisitas orbit asteroid ini tercatat sebesar 0.091, sementara magnitudo mutlaknya adalah 9.7. Pembentukan Seperti asteroid secara ...

2015 soundtrack album Liv and MaddieSoundtrack album by Dove CameronReleasedMarch 17, 2015 (2015-03-17)Recorded2013–2015Genre Power pop pop rock Length45:52LabelWalt DisneyProducerBardur HabergDove Cameron chronology Liv and Maddie(2015) Bloodshot / Waste(2019) Liv and Maddie (Music from the TV Series) is a soundtrack to the Disney Channel Original Series, Liv and Maddie. It features 12 songs performed by the show's star, Dove Cameron and a song performed by Teen Beach Mo...

Genus of plants NothofagusTemporal range: Late Cretaceous to recent 83.6–0 Ma PreꞒ Ꞓ O S D C P T J K Pg N Nothofagus cunninghamii, Eastern Australia. Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Fagales Family: NothofagaceaeKuprian.[1] Genus: NothofagusBlume The range of Nothofagus. Synonyms[2] Calucechinus Hombr. & Jacquinot ex Decne. in J.S.C.Dumont d'Urville Calusparassus Hombr. & ...

Carlo Dalmazzo Carrà Carlo Dalmazzo Carrà (Quargnento, 11 febbraio 1881 – Milano, 13 aprile 1966) è stato un pittore italiano, professore presso l'Accademia di Brera dal 1939 al 1951. Indice 1 Biografia 1.1 Gli inizi 1.2 Il periodo futurista 1.3 Il periodo metafisico 1.3.1 Le figlie di Loth (1919) 1.4 Il periodo trascendente 1.5 Morte 2 Opere 3 Scritti 4 Onorificenze 5 Note 6 Bibliografia 7 Voci correlate 8 Altri progetti 9 Collegamenti esterni Biografia Gli inizi Figlio di un possidente...

Tradisi lisan dalam pengajaran Weda (Sruti) terdiri dari beberapa patha, cara menembangkan mantra-mantra Weda. Keberadaan tradisi pengajaran lisan ini dianggap sebagai tradisi tertua dan tak terputus hingga sekarang, fiksasi dari sastra-sastra Samhita diperkirakan telah dikenal pada masa awal zaman besi.[1] Lihat pula Weda Sruti Samhita Catatan kutipan ^ Scharfe, Hartmut: Education in Ancient India, 2002, BRILL; ISBN 90-04-12556-6, 9789004125568, at Ch. 13: Memorising the Veda, at p. ...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Southern Uí Néill – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Ireland about the year 900 The Southern Uí Néill (Irish: Uí Néill an Deiscirt, IPA:[ˈiːˈnʲeːl̪ʲˈanˠˈdʲɛʃcəɾˠtʲ]) were that branch of...

42°42′N 131°26′E / 42.700°N 131.433°E / 42.700; 131.433 里姆斯基柯薩科夫群島是俄羅斯的群島,位於海參崴西南約70公里的彼得大帝灣,由6座小島和數個岩島組成,行政方面由哈桑區負責管轄,面積約6平方公里,最高點海拔高度144米,該群島在1851年被法國觀鯨人員發現,島上無人居住。 这是一篇與俄罗斯地理相關的小作品。您可以通过编辑或修订扩充其内容。...

此條目部分链接不符合格式手冊規範。跨語言链接及章節標題等處的链接可能需要清理。 (2015年12月12日)請協助改善此條目。參見WP:LINKSTYLE、WP:MOSIW以了解細節。突出显示跨语言链接可以便于检查。 萊斯布里奇Lethbridge市City of Lethbridge萊斯布里奇市中心 旗幟萊斯布里奇萊斯布里奇在亞伯達省的位置坐标:49°41′39″N 112°49′58″W / 49.694167°N 112.832778°W / 49.694167...