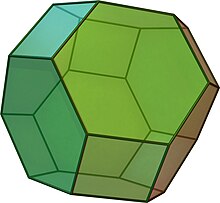
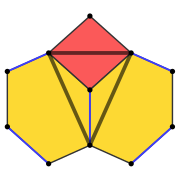
Truncated octahedron
| |||||||||||||||||||||
Read other articles:

Questa voce sull'argomento strumenti musicali è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Un basso elettrico fretless Sandberg Guitars Fretless (dall'inglese senza tasti) indica ogni cordofono sprovvisto di tasti (le traversine metalliche che dividono secondo rapporti costanti la tastiera). Mentre il violino e gli altri strumenti ad arco sono sempre fretless (eccezion fatta per la famiglia della vi...

Cinema ofthe Soviet Union Russian Empire 1908–1917 Lists of Soviet films 1917–1929 1922 1923 1924 19251926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980–1991 1980 1981 1982 1983 19841985 1986 1987 1988 1989 19901991 Russian films 1992–vte ...

Pembaringan kenegaraan Philip IV dari Prancis Pembaringan kenegaraan Mahatma Gandhi Pembaringan kenegaraan adalah sebuah tradisi dimana jasad orang mati ditempatkan di sebuah bangunan kenegaraan, di luar atau di dalam peti mati agar khalayak umum dapat memberikan penghormatan mereka. Kegiatan tersebut biasanya dilakukan di bangunan pemerintahan utama dari sebuah negara, daerah atau kota. Meskipun praktiknya berbeda di tiap negara, jika kegiatannya dilakukan di sebuah lokasi selain gedung peme...

Ongoing COVID-19 viral pandemic in New Hampshire, United States COVID-19 pandemic in New HampshireThe NH National Guard loading boxes of personal protective equipment in Concord DiseaseCOVID-19Virus strainSARS-CoV-2LocationNew Hampshire, U.S.Index caseGrafton CountyArrival dateMarch 2, 2020Confirmed cases344,823[1]Hospitalized cases849 (cumulative)185 (current)Recovered19,864[1]Deaths2,662[1]Government websitewww.nh.gov/covid19 The COVID-19 pandemic in New Hampshire is...

José Manuel Balmaceda Presiden Chili ke-11Masa jabatan18 September 1886 – 29 Agustus 1891 PendahuluDomingo Santa MaríaPenggantiJorge Montt Informasi pribadiLahir(1840-07-19)19 Juli 1840Bucalemu, ChiliMeninggal18 September 1891 (umur 51)Santiago, ChiliPartai politikLiberalSuami/istriEmilia de Toro HerreraTanda tanganSunting kotak info • L • B José Manuel Emiliano Balmaceda Fernández (19 Jul 1840 – 18 September 1891) adalah Presiden Chili ke-11, yang menjabat seja...

Comptroller General's Departmentกรมบัญชีกลางkrom banchi klangAgency overviewFormed7 October 1890TypeGovernment agencyJurisdictionNationwideHeadquartersPhaya Thai, Bangkok, ThailandAgency executiveComptroller-General Mrs.Patricia MongkhonvanitParent agencyMinistry of FinanceWebsitewww.cgd.go.th The Comptroller General's Department (CGD) (Thai: กรมบัญชีกลาง; RTGS: krom banchi klang) is a Thai government agency under the Ministry of Finance.&#...

Indian classical Bharata Natyam dancer Padma SubrahmanyamBorn4 February 1943 (1943-02-04) (age 81)Madras presidency, British IndiaNationalityIndianAlma materEthiraj College for WomenOccupation(s)Dancer, Choreographer, Teacher and AuthorKnown forBharatanatyamParentKrishnaswami Subrahmanyam (father)RelativesS. Krishnaswamy (brother)Raghuram (nephew)Anirudh Ravichander (grand-nephew)Hrishikesh (grand-nephew)Gayathri Raghuram (grand-niece)AwardsPadma Shri (1981) Padma Bhushan ...

Financial aid given to support the development of developing countries In some countries there is more development aid than government spending. (Image from World in Data) Development aid is a type of foreign/international/overseas aid given by governments and other agencies to support the economic, environmental, social, and political development of developing countries.[1] Closely related concepts include: developmental aid, development assistance, official development assistance, ...

Stadion NasionalKokuritsu KyōgijōStadion saat pertandinganJ.League Cup pada 2004Lokasi10-2, Kasumigaoka-machi, Shinjuku, Tokyo, JepangTransportasi umum E25 Kokuritsu-Kyōgijō JB12 SendagayaPemilikDewan Olahraga JepangKapasitas48,000Ukuran lapangan105 m × 68 m (344 ft × 223 ft)PermukaanRumputKonstruksiDibukaMaret 1958; 66 tahun lalu (1958-03)Ditutup31 Mei 2014; 9 tahun lalu (2014-05-31)DihancurkanMei 2015; 9 tahun lalu (2015-05)ArsitekMitsuo Ka...

Agenzia per la sicurezza nucleareStato Italia TipoAutorità per la regolamentazione tecnica, il controllo e l'autorizzazione ai fini della sicurezza di tutte le fasi legate alla realizzazione e gestione delle centrali elettronucleari e alla gestione delle scorie radioattive Istituito2009 daGoverno Berlusconi IV Operativo dal2009 Soppresso2011 daGoverno Monti PresidenteUmberto Veronesi Modifica dati su Wikidata · Manuale L'Agenzia per la sicurezza nucleare è stata, dal 2009 al ...

جزء من سلسلة مقالات حولعلم الاجتماع تاريخ فهرس المواضيع الرئيسية مجتمع عولمة سلوك الإنسان تأثير الإنسان على البيئة هوية الثورات الصناعية 3 / 4 / 5 تعقيد اجتماعي بنائية اجتماعية الثقافة البيئية مساواة اجتماعية إنصاف اجتماعي نفوذ اجتماعي تدرج اجتماعي بنية اجتماعية وجهات نظر ...

Evolusi dari angiospermae menurut Kelompok Filogeni Angiospermae (2013) Kelompok Filogeni Angiospermae (Bahasa Inggris: Angiosperm Phylogeny Group, disingkat menjadi APG) adalah kelompok informal internasional yang terdiri dari ahli botani sistematis yang berkolaborasi untuk membangun konsensus mengenai taksonomi tumbuhan berbunga (angiospermae), yang mencerminkan pengetahuan baru tentang hubungan tumbuhan yang ditemukan melalui studi filogenetik. Pada tahun 2016, empat versi tambahan sistem ...

This article needs to be updated. Please help update this to reflect recent events or newly available information. (December 2020)This article is missing information about transfers. Please expand the article to include this information. Further details may exist on the talk page. (December 2020) 2012–13 CA Osasuna SeasonOsasuna 2012–13 football seasonOsasuna2012–13 seasonPresidentMiguel ArchancoHead coachJosé Luis MendilibarStadiumEl SadarLa Liga16thCopa del ReyRound of 16 Home colou...

Biografi ini tidak memiliki referensi atau sumber sehingga isinya tidak dapat dipastikan. Bantu memperbaiki artikel ini dengan menambahkan sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus.Cari sumber: Cristiano Lucarelli – berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Cristiano Lucarelli Lucarelli pada t...
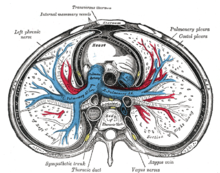
Inflammation of the lungs and pleura Medical conditionPleuropneumoniaLung pleuraSpecialtyPulmonology Pleuropneumonia is inflammation of the lungs and pleura, pleurisy being the inflammation of the pleura alone.[1] See also Contagious bovine pleuropneumonia – a disease in cattle Contagious caprine pleuropneumonia – a disease in goats References ^ Wood, James, ed. (1907). Pleura-pneumonia . The Nuttall Encyclopædia. London and New York: Frederick Warne. Authority control...

Stasiun Yasuushi (安牛駅 Yasuushi-eki) adalah sebuah stasiun kereta api yang berada di Jalur Utama Sōya terletak di Horonobe, Distrik Teshio, Subprefektur Soya, Hokkaido, Jepang, yang dioperasikan oleh JR Hokkaido. Stasiun ini diberi nomor W69. Stasiun Yasuushi安牛駅Bangunan Stasiun YasuushiLokasiKaishin, Horonobe, Distrik Teshio, Prefektur Hokkaido 098-3226, JepangJepangKoordinat44°56′58.5″N 141°53′39″E / 44.949583°N 141.89417°E / 44.949583; 141.894...

Ruler of a Mesoamerican āltepētl (city-state) This article is about tlahtohqueh in general. For the rulers of Tenochtitlan, see List of tlatoque of Tenochtitlan. 17th-century depiction of tlahtoāni Nezahualpiltzintli of Texcoco from the Codex Ixtlilxochitl. Tlahtoāni of Aztec EmpireSacred war emblemDetailsStyleHuēyi tlahtoāniFirst monarchAcamapichtliLast monarchCuauhtémocFormationc. 1376Abolition1521ResidenceTenochtitlanAppointerCouncil of Elders Tlahtoāni[1] (...

1988 NCAA Division IIImen's basketball tournamentFinals siteGrand Rapids, MichiganChampionsOhio Wesleyan Battling Bishops (1st title)Runner-upScranton Royals (3rd title game)SemifinalistsHartwick Hawks (1st Final Four)Nebraska Wesleyan Prairie Wolves (3rd Final Four)Winning coachGene Mehaffey (OWU)MOPScott Tedder (OWU)Attendance34,373 NCAA Division III men's tournaments «1987 1989» The 1988 NCAA Division III men's basketball tournament was the 14th annual single-elimination tournam...

Cet article est une ébauche concernant une localité de l'Alaska. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Fort Yukon La région de Fort Yukon Administration Pays États-Unis État Alaska Borough Région de recensement de Yukon-Koyukuk Code FIPS 02-26760 Démographie Population 583 hab. (2010) Densité 30 hab./km2 Géographie Coordonnées 66° 34′ 03″ nord, 145° 15′&#...

Sheep and fields in Bekaa Valley (2021) Economy of Lebanon Overview Agriculture Banque du Liban Beirut Stock Exchange (listings) Companies Labour movement Shipping Tourism Other topics Culture Environment Geography History People Politics vte Agriculture in Lebanon is the third most productive sector in the country after the tertiary and industrial sectors. It contributes 3.1% of GDP[1] and 8 percent of the effective labor force.[2] The sector includes an informal Syrian labo...