Square pyramid
| |||||||||||||||||||||||||||||
Read other articles:
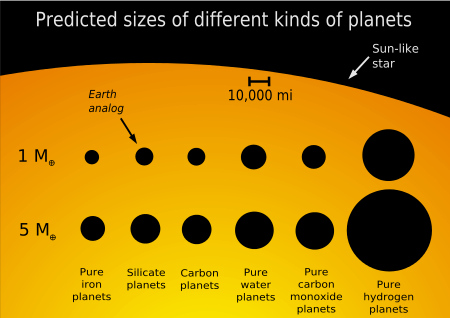
Perbandingan ukuran planet dengan komposisi berbeda Sebuah planet besi adalah sejenis planet yang terdiri dari inti kaya besi dengan sedikit atau tanpa mantel. Merkurius adalah benda angkasa terbesar dari jenis tersebut di Tata Surya. Lihat pula Planet kerdil Planet ekstrasurya Planet kebumian Referensi lbsEksoplanetologi Planet Pengertian IAU Ilmu keplanetan Topik utama Eksoplanet Metode pendeteksian eksoplanet Sistem keplanetan Ukurandan jenisKebumian Planet karbon Planet tanpa inti Planet ...

American politician (1912–1994) Milton ShappShapp in 197640th Governor of PennsylvaniaIn officeJanuary 19, 1971 – January 16, 1979LieutenantErnest P. KlinePreceded byRaymond P. ShaferSucceeded byDick Thornburgh Personal detailsBornMilton Jerrold Shapiro(1912-06-25)June 25, 1912Cleveland, Ohio, U.S.DiedNovember 24, 1994(1994-11-24) (aged 82)Merion, Pennsylvania, U.S.Political partyDemocraticSpouses Harriet Nolte (m. 1939; div. 1947)...

Dirk Lives in Holland AuthorAstrid LindgrenOriginal titleJackie bor i HollandIllustratorAnna Riwkin-BrickCountrySwedenLanguageSwedishSeriesChildren's EverywhereGenreChildren's literaturePublisherRabén & SjögrenPublication date1963Published in English1964Preceded byMarko Lives in Yugoslavia Followed byRandi Lives in Norway Dirk Lives in Holland (original title: Jackie bor i Holland) is the title of a book by the Swedish writer Astrid Lindgren, with photos b...

Pertanian Umum Agribisnis Agroindustri Agronomi Ilmu pertanian Jelajah bebas Kebijakan pertanian Lahan usaha tani Mekanisasi pertanian Menteri Pertanian Perguruan tinggi pertanian Perguruan tinggi pertanian di Indonesia Permakultur Pertanian bebas ternak Pertanian berkelanjutan Pertanian ekstensif Pertanian intensif Pertanian organik Pertanian urban Peternakan Peternakan pabrik Wanatani Sejarah Sejarah pertanian Sejarah pertanian organik Revolusi pertanian Arab Revolusi pertanian Inggris Revo...

The extent of the Indus Valley Civilisation This list of inventions and discoveries of the Indus Valley Civilisation lists the technological and civilisational achievements of the Indus Valley Civilisation, an ancient civilisation which flourished in the Bronze Age around the general region of the Indus River and Ghaggar-Hakra River in what is today Pakistan, and parts of India. Inventions Computer-aided reconstruction of Harappan coastal settlement in Pakistan on the westernmost outreaches ...

Cet article est une ébauche concernant une unité ou formation militaire américaine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. 4th Fighter Wing Blason du 4th Fighter Wing Création 28 juillet 1947 - Aujourd'hui Pays États-Unis Fait partie de USAF Garnison Seymour Johnson AFB Devise Fourth But First Équipement F-15E Commandant historique Chuck Yeager modifier Le 4th Fighter Wing (4th FW, 4e e...

Model anion sianat. Ion sianat adalah anion dengan rumus kimia [OCN]− or [NCO]−. Pada larutan ion ini berperan sebagai basa membentuk asam isosianat, HNCO. Ion sianat membentuk kompleks dengan ion logam di mana atom nitrogen atau oksigen berperan sebagai donor pasangan elektron. Ion sianat Tiga atom-atom pada ion sianat berada pada satu garis lurus sehingga strukturnya linear. Struktur elektroniknya dapat dituliskan sebagai Ö:-C≡N: Dengan ikatan tunggal C-O dan ikatan C-N rangkap tiga....

2005 UNCAF Nations CupTournament detailsHost countryGuatemalaTeams7 (from 1 sub-confederation)Final positionsChampions Costa Rica (5th title)Runners-up HondurasThird place GuatemalaFourth place PanamaTournament statisticsMatches played13Goals scored34 (2.62 per match)Top scorer(s) Wilmer Velásquez(6 goals)← 2003 2007 → International football competition The eighth edition of the bi-annual UNCAF Nations Cup was held in Guatemala, from February 19...

Wine packaged in a bag-in-box arrangement This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (December 2016) (Learn how and when to remove this message) A 4-litre cask of Australian white wine Boxed wine (cask wine) is a wine sold in bag-in-box packaging. Traditionally, this consists of a cardboard box containing a wine filled plastic reservoir. The flow of the wine from the box is controlled ...

Build God, Then We'll TalkLagu oleh Panic! at the Discodari album A Fever You Can't Sweat OutSisi-BBuild God, Then We'll Talk (Live in Denver)[1]Dirilis26 Maret 2007FormatUnduhan digitalDirekam2005GenreBaroque pop, pop punkDurasi3:40LabelDecaydancePenciptaRyan Ross, Brendon Urie, Spencer SmithLirikus Ryan Ross Brendon Urie Spencer Smith ProduserMatt Squire Build God, Then We'll Talk adalah singel kelima sekaligus terakhir dari album debut grup musik Panic! at the Disco, A Fever You Ca...

Voce principale: Unione Sportiva Sanremese Calcio 1904. Unione Sportiva SanremeseStagione 1979-1980Sport calcio Squadra Sanremese Allenatore Ezio Caboni Presidente Gianni Borra Serie C14º posto nel girone A. Maggiori presenzeCampionato: Vella (34) Miglior marcatoreCampionato: Vella (10) 1978-1979 1980-1981 Si invita a seguire il modello di voce Indice 1 Divise 2 Rosa 3 Risultati 3.1 Campionato 3.1.1 Girone di andata 3.1.2 Girone di ritorno 4 Bibliografia Divise 1ª divisa 2ª divisa Ro...

Pour les articles homonymes, voir Gray. Loren GrayBiographieNaissance 19 avril 2002 (22 ans)PottstownNom de naissance AchonchonNationalité américaineActivités Chanteuse, youtubeuse, productrice de télévisionPériode d'activité depuis 2015Autres informationsLabel Virgin MusicDistinction Forbes 30 Under 30 (2021)modifier - modifier le code - modifier Wikidata Loren Gray Beech, née le 19 avril 2002, est une influenceuse, chanteuse, vidéaste et femme d'affaires américaine. Biograph...

English women's association football club Chelsea Women redirects here. For various subjects titled Chelsea Girls, see Chelsea Girl (disambiguation). Football clubChelsea WomenFull nameChelsea Football Club WomenNickname(s)The BluesFounded1992; 32 years ago (1992)[1]GroundKingsmeadowStamford Bridge (select home games)Capacity4,850 (Kingsmeadow)40,173 (Stamford Bridge)OwnerBlueCo[2]ChairmanAdrian Jacob[3]ManagerEmma HayesLeagueWomen's Super League2022�...

哈比卜·布尔吉巴الحبيب بورقيبة第1任突尼斯总统任期1957年7月25日—1987年11月7日(30年105天)总理巴希·拉德加姆(英语:Bahi Ladgham)(1969年-1970年)赫迪·努伊拉(英语:Hedi Nouira)(1970年-1980年)穆罕默德·姆扎利(英语:Mohammed Mzali)(1980年-1986年)拉希德·斯法尔(英语:Rachid Sfar)(1986年-1987年)宰因·阿比丁·本·阿里(1987年)继任宰因·阿比丁·本·...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hankai Uemachi Line – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Uemachi LineUemachi Line tramOverviewLocaleOsakaTerminiTennoji-ekimaeSumiyoshiStations10ServiceTypetramServices2Operator(s)Hankai Tramw...

「アプリケーション」はこの項目へ転送されています。英語の意味については「wikt:応用」、「wikt:application」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年4月) 古い情報を更新する必要があります。(2021年3月)出...

This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (December 2023) (Learn how and when to remove this message) American HindusHoli celebration at Sri Sri Radha Krishna Temple in Spanish Fork, UtahTotal population3,369,976 (2021) [1][2]1% of U.S. Population[3](2016 Public Religion Research Institute data) 0.7% of the U.S. Population (2015 Pew Research Center data)[4]Regions with significant popul...

American politician and businessman (1945–2019) Bob HannerMember of the Georgia House of RepresentativesIn officeSeptember 18, 1975 – January 14, 2013Preceded byJohn R. Irwin IIISucceeded byDistrict abolishedConstituency130th district (1975–1983)131st district (1983–1993)159th district (1993–2003)133rd district (2003–2005)148th district (2005–2013) Personal detailsBornRobert Paul Hanner(1945-04-19)April 19, 1945Americus, Georgia, U.S.DiedJanuary 2, 2019(2019-01-02) (age...

Запрос «Украинец» перенаправляется сюда; см. также другие значения. У этого термина существуют и другие значения, см. Украинцы (значения). Украинцы Современное самоназвание українці[1] Численность и ареал Всего: ок. 45 млн чел. Украина: 37 541 693 (перепись 2001)[2][3&#...

Climate change in the US state of South Dakota Köppen climate types in South Dakota showing the state to be largely hot-summer humid continental. Climate change in South Dakota encompasses the effects of climate change, attributed to man-made increases in atmospheric carbon dioxide, in the U.S. state of South Dakota. Due to South Dakota's location in the Northern Great Plains, the effects of climate change will vary from eastern South Dakota to western South Dakota. Eastern South Dakota can ...













































