Surface area
|
Read other articles:

Stasiun Shiogama塩釜駅Stasiun Shiogama, April 2009Lokasi 5-1 Higashi-Tamagawa-cho, Shiogama-shi, Miyagi-ken 985-0042JepangKoordinat38°18′33″N 141°00′33″E / 38.3092°N 141.0092°E / 38.3092; 141.0092Koordinat: 38°18′33″N 141°00′33″E / 38.3092°N 141.0092°E / 38.3092; 141.0092Operator JR EastJalur ■ Jalur Utama Tōhoku ■ Jalur Senseki-Tōhoku Letak365.2 km dari TokyoJumlah peron1 peron pulauJumlah jalur2Informasi lain...

صربيا والجبل الأسود Državna Zajednica Srbija i Crna Gora Државна Заједница Србија и Црна Гора جمهورية يوغوسلافيا الاتحادية اتحادا في جمهورية 1992 – 2006 صربيا والجبل الأسودعلم صربيا والجبل الأسودشعار موقع الجمهورية في أوروبا عاصمة بلغراد نظام الحكم جمهورية اشتراكية اللغة الرسمي�...

Sporetus colobotheides Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Subfamili: Lamiinae Tribus: Acanthocinini Genus: Sporetus Spesies: Sporetus colobotheides Sporetus colobotheides adalah spesies kumbang tanduk panjang yang tergolong famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Sporetus, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu ...

Disambiguazione – Renato Rossini rimanda qui. Se stai cercando il calciatore, vedi Renato Rossini (calciatore). Questa voce sugli argomenti attori italiani e sceneggiatori italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Ross nel film 5 bambole per la luna d'agosto (1970) Renato Rossini, noto come Howard Ross, o Red Ross (Roma, 10 gennaio 1941), è un attore e sceneggiatore italiano. ...

2019 Référendum cubain de 2022 25 septembre 2022 Corps électoral et résultats Inscrits 8 457 978 Votants 6 269 427 74,12 % Blancs et nuls 360 042 Nouveau code de la famille Pour 66,85 % Contre 33,15 % modifier - modifier le code - voir Wikidata Le référendum cubain de 2022 a lieu le 25 septembre 2022 afin de permettre à la population de Cuba de se prononcer sur un nouveau code de la famille légalisant notamment ...

UFC mixed martial arts event in 2019 UFC Fight Night: Assunção vs. Moraes 2The poster for UFC Fight Night: Assunção vs. Moraes 2InformationPromotionUltimate Fighting ChampionshipDateFebruary 2, 2019 (2019-02-02)VenueCentro de Formação Olímpica do NordesteCityFortaleza, BrazilAttendance10,040[1]Event chronology UFC 233 (cancelled) UFC Fight Night: Assunção vs. Moraes 2 UFC 234: Adesanya vs. Silva UFC Fight Night: Assunção vs. Moraes 2 (also known as UFC Fight ...

English philosopher and Christian apologist Richard SwinburneProfessorSwinburne in 2009BornRichard Granville Swinburne (1934-12-26) 26 December 1934 (age 89)Smethwick, EnglandAcademic backgroundAlma materExeter College, OxfordInfluences Plato Aristotle René Descartes Thomas Aquinas Rudolf Carnap Carl Hempel Academic workDisciplinePhilosophytheologySub-disciplinePhilosophical theologyphilosophy of religionphilosophy of scienceSchool or traditionAnalytic philosophyInstitutionsUniversity o...

Didone abbandonata, act 1, scene 5; Francesco Battaglioli (1754) Didone abbandonata is an opera libretto in three acts by Pietro Metastasio. It was his first original work and was set to music by Domenico Sarro in 1724. The opera was accompanied by the intermezzo L'impresario delle Isole Canarie, also by Metastasio. During the century that followed, it was set more than 50 times by other composers such as Nicola Porpora (1725), Leonardo Vinci (1726), Baldassare Galuppi (1740), Johann Adolph H...

American singer and songwriter For technical reasons, Judy Collins #3 redirects here. For the album, see Judy Collins 3. Judy CollinsCollins at the Cambridge Folk Festival, 2008Background informationBirth nameJudith Marjorie CollinsBorn (1939-05-01) May 1, 1939 (age 85)Seattle, Washington, U.S.OriginDenver, Colorado, U.S.GenresFolkAmericanacountryrock and rollpopOccupation(s)SingersongwritermusicianInstrument(s)VocalspianoguitarYears active1959–presentLabelsElektraGeffenMCAMesa Bluemoo...
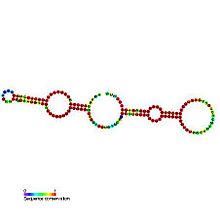
Small nucleolar RNA psi28S-1192Predicted secondary structure and sequence conservation of snopsi28S-1192IdentifiersSymbolsnopsi28S-1192RfamRF00542Other dataRNA typeGene; snRNA; snoRNA; HACA-boxDomain(s)EukaryotaGOGO:0006396 GO:0005730SOSO:0000594PDB structuresPDBe In molecular biology, Small nucleolar RNA psi28S-1192 (also known as snoRNA psi28S-1192) is a non-coding RNA (ncRNA) molecule which functions in the biogenesis (modification) of other small nuclear RNAs (snRNAs). This type of modify...

Il piccolo Nicolas e i suoi genitoriGli alunni si mettono in posa per la foto di classe, Nicolas è al centro con indosso un maglioncino rosso.Titolo originaleLe Petit Nicolas Lingua originalefrancese Paese di produzioneFrancia Anno2009 Durata91 min e 90 min Rapporto1,85:1 Generecommedia RegiaLaurent Tirard SoggettoJean-Jacques Sempé, René Goscinny SceneggiaturaLaurent Tirard, Grégoire Vigneron, Alain Chabat ProduttoreEric Jehelmann Casa di produzioneFidélité Productions Distribuzione in...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Пушка — негеральдическая искусственная гербовая фигура, возникшая изначально в шведской и русской геральдике в Новое время с XVII века. В геральдике почти без исключений артиллерийское орудие этого типа представляется на раннем этапе своего развития — не казнозар...

U.S. Navy sailors exercising in the presence of a female fitness instructor, 2010 A professional fitness coach is a professional in the field of fitness and exercise, most often instruction (fitness instructor), including professional sports club's fitness trainers and aerobics and yoga instructors and authors of fitness instruction books or manuals. Overview Fitness topics may also include nutrition, weight-loss, and self-help. Fitness careers are distinguished from exercise science careers ...

Die-in by I BIKE Dublin at Dublin City Council, 2019, in Dublin Czech poster 1902 Activities promoting cycling Cycling advocacy consists of activities that call for, promote or enable increased adoption and support for cycling and improved safety and convenience for cyclists, usually within urbanized areas or semi-urban regions. Issues of concern typically include policy, administrative and legal changes (the consideration of cycling in all governance); advocating and establishing better cycl...

حرب البوير الثانية جزء من حروب البوير جنود بريطانيون على أعتاب مدينة ليديسميث، 1900. معلومات عامة التاريخ وسيط property غير متوفر. بداية 11 أكتوبر 1899 نهاية 31 مايو 1902 البلد مدينية ليدي سمث في جنوب افريقيا الموقع جنوب أفريقيا، سوازيلاند[1] المتحاربون الإمبراطورية البريط�...

Bataillon envoyé au front sur la route de la gare de Biləcəri en 1942. La République socialiste soviétique d'Azerbaïdjan entre dans la Seconde Guerre mondiale après l'invasion allemande de l'Union soviétique le 22 juin 1941. Les champs pétrolifères azerbaïdjanais attiraient les Allemands en raison de la forte dépendance de l'URSS vis-à-vis du pétrole du Caucase – préparant le terrain pour les campagnes allemandes tentant de capturer et de s'emparer des champs pétrolifères d...

1916 battle on the Eastern Front of WWI Battle of KostiuchnówkaPart of the Brusilov Offensive during the First World WarPolish Legionnaires at KostiuchnówkaDateJuly 4–7, 1916LocationKostiuchnówka (Kostyukhnivka)51°20′35″N 25°45′35″E / 51.34306°N 25.75972°E / 51.34306; 25.75972Result InconclusiveBelligerents Austria-Hungary(Polish Legions) Russian EmpireCommanders and leaders Józef Piłsudski Alexey KaledinStrength 5,500[1]–7,300[2&...

A large artificial harbour of Ancient Rome For other uses, see Portus (disambiguation) and Porto (disambiguation). PortusThe mouth of the Tiber, with the hexagonal harbour of Portus at upper middle (modern day Lago Traiano).Click on the map to see markerRegionLazioCoordinates41°46′44″N 12°15′32″E / 41.779°N 12.259°E / 41.779; 12.259TypeSettlement, PortHistoryPeriodsRoman RepublicRoman EmpireCulturesAncient RomeSite notesExcavation datesyesArchaeologist...

See also: Invasion of Jersey (1779) Franco-Spanish naval enterprise against Britain Armada of 1779Part of the American Revolutionary WarDateJune to September 1779LocationEnglish ChannelResult British victory[1][2]Belligerents France Spain Great BritainCommanders and leaders Comte d'Orvilliers Comte de Vaux Luis de Córdova y Córdova Sir Charles Hardy Lord AmherstStrength 66 ships of the line30,000 troops[3] 38 ships of the line20,000 troops39,000 militia&#...








































