Censoring (statistics)
|
Read other articles:

Tempat penyimpanan gas alam. Sumber daya alam ini menjadi asal mula munculnya istilah dutch disease. Penyakit Belanda (bahasa Inggris: Dutch disease) adalah fenomena di bidang perekonomian yang merujuk pada dampak yang biasanya ditimbulkan oleh berlimpahnya sumber daya alam di suatu negara.[1] Istilah ini dikemukakan pertama kali pada tahun 1977, yang merujuk pada menurunnya pertumbuhan di sektor perindustrian secara drastis akibat ditemukannya sumber gas alam yang berlimpah di Be...

Parochial, coeducational school in Perryville, , Missouri, United StatesSt. Vincent High SchoolAddress210 South Waters StreetPerryville, (Perry County), Missouri 63775United StatesCoordinates37°43′23″N 89°52′30″W / 37.72306°N 89.87500°W / 37.72306; -89.87500InformationTypeParochial, CoeducationalMottoReligio ∙ Scientia ∙ Cultura(Religion ∙ Knowledge ∙ Culture)Religious affiliation(s)Roman CatholicPatron saint(s)St. Vincent DePaulEstablished1896Super...

Town in Indiana, United StatesOsgood, IndianaTownThe Damm Theatre in Downtown OsgoodLocation of Osgood in Ripley County, Indiana.Coordinates: 39°07′32″N 85°17′36″W / 39.12556°N 85.29333°W / 39.12556; -85.29333CountryUnited StatesStateIndianaCountyRipleyTownshipCenterArea[1] • Total1.58 sq mi (4.11 km2) • Land1.55 sq mi (4.01 km2) • Water0.04 sq mi (0.09 km2)Elevation&#...

Vignette CorporationIndustrySoftwareFounded1995; 29 years ago (1995)FounderRoss Garber Neil WebberDefunctJuly 21, 2009; 14 years ago (2009-07-21)FateAcquired by Open Text CorporationHeadquartersAustin, Texas Vignette Corporation was a company that offered a suite of content management, web portal, collaboration, document management, and records management software. Targeted at the enterprise market, Vignette offered products under the name StoryServer that ...

Chronologies Données clés 1954 1955 1956 1957 1958 1959 1960Décennies :1920 1930 1940 1950 1960 1970 1980Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égyp...

Supercopa andorrana 2017 Competizione Supercopa andorrana Sport Calcio Edizione 15ª Organizzatore Federazione calcistica di Andorra Date 10 settembre 2017 Luogo Andorra Partecipanti 2 Formula Partita unica Risultati Vincitore FC Santa Coloma(6º titolo) Secondo UE Santa Coloma Cronologia della competizione 2016 2018 Manuale La Supercopa andorrana 2017 è stata la quindicesima edizione della supercopa andorrana di calcio. La partita è stata giocata dall'FC Santa Coloma, vincitore del ...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Pour les articles homonymes, voir Pays-Bas (homonymie). Ne doit pas être confondu avec la Hollande. Royaume des Pays-Bas(nl) Koninkrijk der Nederlanden Drapeau des Pays-Bas Armoiries des Pays-Bas Devise Je maintiendrai Hymne en néerlandais : Wilhelmus van Nassouwe (« Guillaume de Nassau ») Fête nationale 27 avril[Note 1] · Événement commémoré Anniversaire du roi régnant Le Royaume des Pays-Bas en Europe (l’Union européenne en vert clair). Administr...

这是马来族人名,“尤索夫”是父名,不是姓氏,提及此人时应以其自身的名“法迪拉”为主。 尊敬的拿督斯里哈芝法迪拉·尤索夫Fadillah bin Haji YusofSSAP DGSM PGBK 国会议员 副首相 第14任马来西亚副首相现任就任日期2022年12月3日与阿末扎希同时在任君主最高元首苏丹阿都拉陛下最高元首苏丹依布拉欣·依斯迈陛下首相安华·依布拉欣前任依斯迈沙比里 马来西亚能源转型与�...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

English politician (1804–1865) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Richard Cobden – news · newspapers · books · scholar · JSTOR (December 2022) (Learn how and when to remove this message) Richard CobdenCobden c. early 1860sParliamentary offices1841–1847Member of Parliament for Stockport1847�...

One of the first stamps of Nova Scotia issued 1851. This is a survey of the postage stamps and postal history of Nova Scotia. First stamps The first stamps of Nova Scotia were issued in 1851.[1] 1863 issue in cents Values 1 to 12+1⁄2 cents. 2 cents issued 1863. Nova Scotia joined the Dominion of Canada in 1867. See also List of people on stamps of the Canadian provinces Postage stamps and postal history of Canada References ^ Stanley Gibbons Stamp Catalogue: Commonwealth and Br...

Questa voce sull'argomento fisici statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Robert Williams Wood Robert Williams Wood (Concord, 2 maggio 1868 – Amityville, 11 agosto 1955) è stato un fisico e inventore statunitense. Indice 1 Biografia 2 Onorificenze 3 Altri progetti 4 Collegamenti esterni Biografia I suoi studi furono volti alla spettroscopia, alla fosforescenza e alla diffrazione sebbene sia maggiormente noti i suoi lavori sulla...

2013 Singaporean filmGhost ChildTheatrical release posterDirected byGilbert ChanWritten byGilbert ChanTang Fong ChengDanny YeoScreenplay byTan Fong ChengGilbert ChanProduced byGary GohEric KhooTang Fong ChengBert Tan (Executive Producer)StarringChen HanweiJayley WooCarmen SooCinematographyKevin Kee HoeEdited byNatalie SohMusic byKen ChongProductioncompaniesGorylah PicturesClover FilmsMm2 EntertainmentDistributed byGolden Village PicturesRelease date 7 March 2013 (2013-03-07)&#...

The following is a list of football stadiums in Albania, ranked by seating capacity. The minimum capacity is 1,000. Current stadiums Rank Stadium City Capacity Home team(s) Opened Image 1 Arena Kombëtare Tiranë 22,500 Albania NT 2019 2 Loro Boriçi Stadium Shkodër 16,000 Albania NT, Vllaznia 1953, 2016 3 Tomori Stadium Berat 14,890 Tomori 1985 4 Elbasan Arena Elbasan 12,800 Albania NT, KF Elbasani 1967, 2014 5 Skënderbeu Stadium Korçë 12,343 Skënderbeu 1957 6 Niko Dovana Stadium Durr�...

Cet article est une ébauche concernant la médecine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juin 2009). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en ...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. هذا المقال جزء من سلسلة عنالطب البديل والعلوم الزائفة معلومات عامة طب بديل طب بيطري بديل الدجل (الخداع الطبي) تاريخ الطب البديل تاريخ الطب العلوم الزائفة مناهضة العلم شكوكية ...
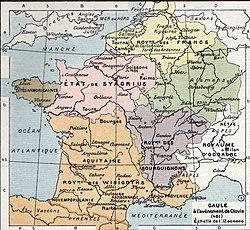
Halaman ini berisi artikel tentang perkembangan geografi dan politik dari wilayah kekuasaan orang Franka. Untuk suku bangsa dan masyarakat Franka, lihat Suku Franka. Untuk kegunaan lain, lihat Franka. Kerajaan Orang FrankaRegnum Francorumcode: la is deprecated (Latin)Riki Frankscode: fr is deprecated (Prancis)481–843 Lebah MaduLambang kebesaran wangsa Meroving Peta diakronik dari keseluruhan wilayah yang pernah dikuasai orang FrankaStatusKekaisaranIbu kota Tournai (4...

Part of a series onAncientMesopotamian religionChaos Monster and Sun God Religions of the ancient Near East Anatolia Ancient Egypt Mesopotamia Babylonia Sumer Iranian Semitic Arabia Canaan Primordial beings Tiamat and Abzu Lahamu and Lahmu Kishar and Anshar Mummu Seven gods who decree Four primary Anu Enlil Enki Ninhursag Three sky gods Inanna/Ishtar Nanna/Sin Utu/Shamash Other major deities Adad Dumuzid Enkimdu Enmesharra Ereshkigal Ki Kingu Geshtinanna Lahar Marduk Nergal Ninurta Šulpae M...

هذه المقالة عن المنصورية بالمغرب. لمعانٍ أخرى، طالع المنصورية (توضيح). المنصورية (المغرب) المنصورية[1](بالفرنسية: El Mansouria)[1] تقسيم إداري البلد المغرب[2] الجهة الإقتصادية الدار البيضاء - سطات المسؤولون الإقليم إقليم بن سليمان الدائرة الإدارية ؟؟�...































