Bernoulli scheme
|
Read other articles:

Tari kuda Gipang di Banjar Kuda Gipang atau Kuda Gepang merupakan salah satu kesenian Kuda Lumping yang berupa tarian berbaris menggunakan Eblek anayaman bambu berbentuk hewan kuda berkembang di lingkungan masyarakat Banjar, Kalimantan Selatan. Asal mula Bermula ketika Kerajaan Daha di Banjar dibantu oleh kesultanan Demak dalam kemelut perang perebutan tahta, yang dimana pihak Kesultan Demak memberikan syarat kepada Pangeran Samudera sebagai pewaris tahta kerajaan Daha penerus yang sah untuk ...

Alexander HerrmannHerrmann AgungLahir(1844-02-10)10 Februari 1844Paris, PrancisMeninggal17 Desember 1896(1896-12-17) (umur 52)Ellicottville, New York, ASPekerjaanpesulap, ilusionis Alexander Herrmann (10 Februari 1844 – 17 Desember 1896)[1] adalah seorang pesulap asal Prancis, yang lebih dikenal sebagai Herrmann Agung. Ia menikahi Adelaide Herrmann, pesulap lain yang dikenal sebagai Ratu Sulap. Referensi ^ Magician Herrmann Dead (PDF). The New York Times. Decembe...

Constituency of Bangladesh's Jatiya Sangsad Brahmanbaria-1Constituencyfor the Jatiya SangsadDistrictBrahmanbaria DistrictDivisionChittagong DivisionElectorate214,039 (2018)[1]Current constituencyCreated1984PartyindependentMember(s)Syed AK Ekramuzzaman Brahmanbaria-1 is a constituency represented in the Jatiya Sangsad (National Parliament) of Bangladesh since January 2024 by Syed A.K. Ekramuzzaman of the independent politician . Boundaries The constituency encompasses Nasirnagar Upazil...

Quodlibet dari buku lagu Hieronymus Lauweryn Watervliet Quodlibet adalah nama yang pertama kali diberikan oleh Wolfgang Schmeltzl pada tahun 1554 kepada komposisi yang terdiri dari banyak suara, sering kali vokal, dipadu dari berbagai fragmen nyanyian atau lagu yang saat itu dikenal.[1] Disusun agar terdengar kocak, bisa dinyanyikan serempak, sambung menyambung atau berganti-ganti.[1] Quodlibet terutama populer pada abad ke-15 dan ke-16.[2] Quodlibet yang terkenal adal...

العلاقات الدومينيكانية الكوستاريكية جمهورية الدومينيكان كوستاريكا جمهورية الدومينيكان كوستاريكا تعديل مصدري - تعديل العلاقات الدومينيكانية الكوستاريكية هي العلاقات الثنائية التي تجمع بين جمهورية الدومينيكان وكوستاريكا.[1][2][3][4][5]...

Species of plant Not to be confused with Mrs. Burns' Lemon basil, a cultivar of Ocimum basilicum. Lemon basil Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Asterids Order: Lamiales Family: Lamiaceae Genus: Ocimum Species: O. × africanum Binomial name Ocimum × africanumLour. Synonyms[1] Ocimum americanum var. pilosum (Willd.) A.J.Paton Ocimum basilicum var. anisatum Benth. Ocimum basilicum var. pilosum (Willd.) ...

This article is about the municipality in Åland. For the district of Helsinki, see Kulosaari. Municipality in Åland, FinlandBrändöMunicipalityBrändö kommun Coat of armsLocation of Brändö in FinlandBrändöLocation in ÅlandCoordinates: 60°24′42″N 21°2′42″E / 60.41167°N 21.04500°E / 60.41167; 21.04500Country FinlandRegionÅlandSub-regionArchipelago sub-regionCharter1866Government • Municipal managerJohn WredeArea (2018-01-01) ...

الألعاب الأولمبية الشتوية 2022 بكين، الصين الدول المشاركة 91 الرياضيون المشاركون 2786 [1]، و91 [1] المسابقات 109، في 7 رياضة انطلاق الألعاب 4 فبراير المفتتح الرسمي الرئيس شي جين بينغ (متوقع) الملعب ملعب بكين الوطني الاختتام 20 فبراير الموقع الرسمي الموقع الرسمي بيو�...

Ethnic group in Sudan Ethnic group Sudanese GreeksΈλληνες του ΣουδάνThe ceremony hall of the Hellenic Community in Khartoum (2015)Regions with significant populationsSudanLanguagesGreek · Sudanese Arabic · EnglishReligionGreek Orthodox ChurchRelated ethnic groupsAfrican Greeks · Egyptian Greeks · Ethiopian Greeks The Sudanese Greeks, or Greeks in Sudan, are ethnic Greeks from modern-day Sudan; they are small in number (es...
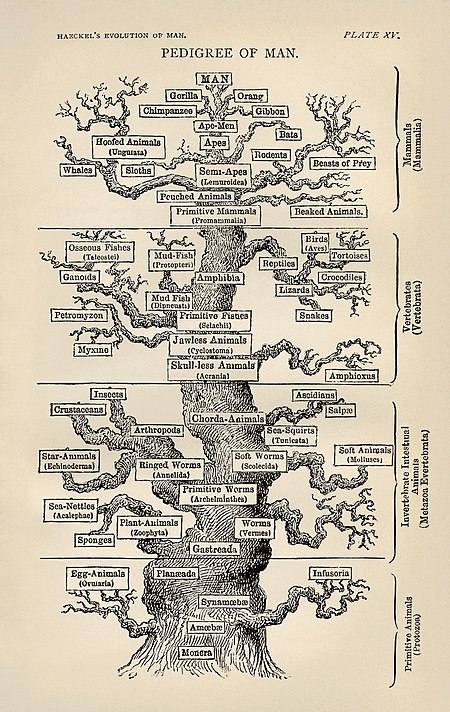
Interdisciplinary area of study For the academic journal, see Human Biology (journal). For the textbook, see Human Biology (textbook). Human biology is an interdisciplinary area of academic study that examines humans through the influences and interplay of many diverse fields such as genetics, evolution, physiology, anatomy, epidemiology, anthropology, ecology, nutrition, population genetics, and sociocultural influences.[1] It is closely related to the biomedical sciences, biological...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. بيث شيلاني مملكة بيث - شيلاني أو بيث شعلاني : Beth-Shilani عاصمتُها ( سَر أنابا Sar-Anaba ) في سنة 732 ق . م قاد الملكُ الآشوري ( تكلتبيلاصر الثالث 745 - 727 ق . م ) حملةً عسكرية على عاصمتِها سر أ...

Village in Dorset, England Human settlement in EnglandPiddletrenthidePiddletrenthidePiddletrenthideLocation within DorsetArea25.54 km2 (9.86 sq mi)Population647 (Parish, 2011)[1]• Density25/km2 (65/sq mi)OS grid referenceST703000Unitary authorityDorsetShire countyDorsetRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townDorchesterPostcode districtDT2PoliceDorsetFireDorset and WiltshireAmbulanceSouth Western ...

Polissena SforzaSignora consorte di RiminiStemma In carica1442-1449 PredecessoreGinevra d'Este SuccessoreIsotta degli Atti NascitaMortara, 1428 MorteRimini, 1º giugno 1449 SepolturaRimini Luogo di sepolturaTempio malatestiano DinastiaSforza PadreFrancesco Sforza MadreGiovanna d'Acquapendente ConsorteSigismondo Pandolfo Malatesta FigliGaleotto, Giovanna Ducato di MilanoCasato degli Sforza Francesco I Figli Galeazzo Maria Ippolita Maria Filippo Maria Sforza Maria Ludovico Maria Elisabett...

United Nations resolution adopted in 1998 UN Security CouncilResolution 1178Ayia Napa beach in southern CyprusDate29 June 1998Meeting no.3,898CodeS/RES/1178 (Document)SubjectThe situation in CyprusVoting summary15 voted forNone voted againstNone abstainedResultAdoptedSecurity Council compositionPermanent members China France Russia United Kingdom United StatesNon-permanent members Bahrain Brazil Costa Rica Gabon Gambia Japan Ke...

Spanish novelist, poet, and playwright (1547–1616) Cervantes redirects here. For other uses, see Cervantes (disambiguation). Miguel Cervantes redirects here. For the American actor and singer, see Miguel Cervantes (actor). Miguel de CervantesThis portrait, attributed to Juan de Jáuregui,[a] is unauthenticated. No authenticated image of Cervantes exists.[1][2]Born(1547-09-29)September 29, 1547Alcalá de Henares, SpainDied22 April 1616(1616-04-22) (aged 68)[3...

Movistar Open 1995Sport Tennis Data23 ottobre – 30 ottobre Edizione3a SuperficieTerra rossa CampioniSingolare Sláva Doseděl Doppio Jiří Novák / David Rikl 1994 1996 Il Movistar Open 1995 è stato un torneo di tennis giocato sulla terra rossa. È stata la 3ª edizione del torneo, che fa parte della categoria ATP World Series nell'ambito dell'ATP Tour 1995.Si è giocato a Santiago in Cile dal 23 al 30 ottobre 1995. Indice 1 Campioni 1.1 Singolare maschile 1.2 Doppio maschile 2 Collegamen...

「浜松医科大学」あるいは「浜松学院大学」とは異なります。 浜松大学 キャンパス(2009年7月)大学設置/創立 1988年廃止 2016年学校種別 私立設置者 学校法人常葉学園本部所在地 静岡県浜松市北区都田町1230北緯34度48分52.85秒 東経137度42分31.88秒 / 北緯34.8146806度 東経137.7088556度 / 34.8146806; 137.7088556座標: 北緯34度48分52.85秒 東経137度42分31.88秒 / ...

Novembre 1869 Nombre de jours 30 Premier jour Lundi 1er novembre 18691er jour de la semaine 44 Dernier jour Mardi 30 novembre 18692e jour de la semaine 48 Calendrier novembre 1869 Sem Lu Ma Me Je Ve Sa Di 44 1er 2 3 4 5 6 7 45 8 9 10 11 12 13 14 46 15 16 17 18 19 20 21 47 22 23 24 25 26 27 28 48 29 30 1869 • Années 1860 • XIXe siècle Mois précédent et suivant Octobre 1869 Décembre 1869 Novembre précédent et suivant Novembre 1868 Novembre 1870 Chronologies...

Scottish industrialist George LauderBornNovember 11, 1837 (1837-11-11)Dunfermline, Fife, ScotlandDiedAugust 24, 1924(1924-08-24) (aged 86)Greenwich, Connecticut, United StatesResting placePutnam CemeteryOther namesDodAlma materUniversity of GlasgowOccupation(s)IndustrialistMechanical EngineerKnown forRevolutionizing the steel industry as a partner at Carnegie SteelSpouseAnna Maria Romeyn VarickChildren3ParentsGeorge Lauder, Sr. (father)Seaton Morrison (mother)FamilyLa...

Pour les articles homonymes, voir Yellowknife (homonymie). Yellowknife (dgr) Sǫ̀mbak’è Administration Pays Canada Province Territoires du Nord-Ouest Région Slave Nord Subdivision régionale 6 Statut municipal Ville Mairesse Mandat Rebecca Alty 2018 - Constitution 1936 et 1er janvier 1970 Démographie Gentilé Yellowknifien, Yellowknifienne Population 20 340 hab. (2021 ) Densité 193 hab./km2 Géographie Coordonnées 62° 27′ nord, 114° 24′ ouest ...







![{\displaystyle [x_{0},x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13bb30613cca27019537eb279c969dc709ad5a9e)
![{\displaystyle \mu \left([x_{0},x_{1},\ldots ,x_{n}]\right)=\prod _{i=0}^{n}p_{x_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9e9cc0afee2887ef5fd889c52b7fe9c6566855c)
![{\displaystyle \mu \left([x_{0},x_{1},\ldots ,x_{n}]\right)=\mathrm {Pr} (X_{0}=x_{0},X_{1}=x_{1},\ldots ,X_{n}=x_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fb255d0c465ff18a82d9b19f6e2267b2cd0064d)




























![{\displaystyle [G\to Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0999961f89f6fed1551f8892d1689cc91d6549a9)






