Baudhayana sutras
|
Read other articles:

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Tinju padaPekan Olahraga Nasional XIX Putra Putri 46 kg 48 kg 49 kg 51 kg 52 kg 54 kg 56 kg 57 kg 60 kg 60 kg 64 kg 64 kg 69 kg 75 kg 81 kg 91 kg Tinju kelas ringan putri pada Pekan Olahraga Nasional XIX akan dilaksanakan di GSG Tinju Pelabuhan Ratu, Kabupaten Sukabumi, Jawa Barat.[1] Jadwal Seluruh waktu menggunakan Waktu Indonesia Barat (UTC+07:00) Tanggal Babak 23 September Perempat final 24 September Semifinal 27 September Final Hasil Perempat final Se...

Artikel ini bukan mengenai lempar lembing. Ilustrasi seseorang yang berusaha melempar seekor kambing Lempar kambing (dalam bahasa Spanyol: Lanzamiento de cabra desde campanario atau Salto de la cabra) adalah sebuah festival di Manganeses de la Polvorosa, provinsi Zamora, Spanyol. Festival ini dirayakan pada hari Minggu keempat bulan Januari. Dalam festival ini sekelompok pemuda akan melemparkan seekor kambing hidup dari atap sebuah gereja. Kerumunan di bawah kemudian akan mencoba menangkap ka...

Untuk merek yang sekarang ditangani oleh Indosat secara langsung, lihat IM3. PT Indosat Multimedia MobileSlogan: No LimitsNama dagangIndosat-M3JenisAnak perusahaanIndustriTelekomunikasiNasibMerger dengan PT Indosat TbkPenerusIndosatDidirikan25 Juli 2001PendiriIndosatDitutup20 November 2003KantorpusatJakarta, IndonesiaTokohkunciHasnul Suhaimi (Mantan Direktur Utama)ProdukOperator seluler GSMMerekBRIGHT (pascabayar)SMART (prabayar)PemilikIndosat PT Indosat Multimedia Mobile (disingkat Indosat-M...

العلاقات المجرية النرويجية المجر النرويج المجر النرويج تعديل مصدري - تعديل العلاقات المجرية النرويجية هي العلاقات الثنائية التي تجمع بين المجر والنرويج.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة الم�...

Marsekal YugoslaviaJosip Broz TitoTito saat berkunjung ke India tahun 1954. Presiden Yugoslavia ke-1Masa jabatan14 Januari 1953 – 4 Mei 1980Perdana MenteriJosip Broz Tito (1953–1963)Petar Stambolić (1963–1967)Mika Špiljak (1967–1969)Mitja Ribičič (1969–1971)Džemal Bijedić (1971–1977)Veselin Đuranović (1977–1980)Wakil PresidenAleksandar Ranković (1963–1966)Koča Popović (1966–1967) PendahuluIvan Ribar(sebagai Presiden Kepresidenan Majelis Rakyat Republi...

Gunboat of the United States Navy For other ships with the same name, see USS Rhode Island. The only known photo of the USS Rhode Island, taken in 1866. History United States NameUSS Rhode Island Laid down1860, as John P. King Launched6 September 1860[1] Acquiredby purchase, 27 June 1861 Commissioned29 July 1861 Decommissioned21 April 1864 Renamed Eagle, 1861 Rhode Island, 29 July 1861 Commissioned3 October 1864 Decommissioned1867 RenamedCharleston, 8 November 1867 Fate Sold for merch...

Response from the Chinese government to COVID-19 Part of a series on theCOVID-19 pandemicScientifically accurate atomic model of the external structure of SARS-CoV-2. Each ball is an atom. COVID-19 (disease) SARS-CoV-2 (virus) Cases Deaths Timeline 2019 2020 January responses February responses March responses April responses May responses June responses July responses August responses September responses October responses November responses December responses 2021 January responses February ...

ХуторЯрской 2-й Центр хутора 49°36′15″ с. ш. 42°37′40″ в. д.HGЯO Страна Россия Субъект Федерации Волгоградская область Муниципальный район Кумылженский Сельское поселение Краснянское История и география Тип климата Умеренно континентальный Часовой пояс UTC+3:00 На...

Universitas Thammasatมหาวิทยาลัยธรรมศาสตร์Nama sebelumnyaUniversitas Moral dan Ilmu PolitikMoto dalam bahasa IndonesiaUntuk keunggulan, keadilan, dan kesiapan dalam kepemimpinan (resmi) Saya mencintai Thammasat karena Thammasat mengajarkan saya untuk mencintai rakyat (tidak resmi)JenisNasionalDidirikan27 Juni 1934 (1934-06-27)PendiriPridi BanomyongRektorProf. Dr. Somkit LertpaithoonStaf administrasi1.505 (2007)[1]Jumlah mahasiswa33.4...
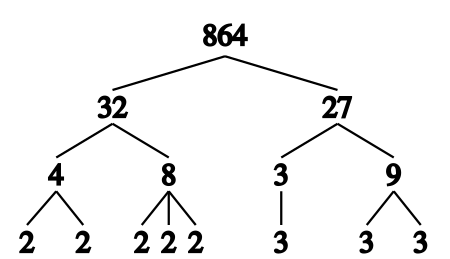
Это изображение демонстрирует нахождение простых множителей числа 864. Сокращённый способ написания — 25 × 33 В теории чисел, простые множители (простые делители) положительного целого числа — это простые числа, которые делят это число нацело (без остатка)[1]....

.912-.875 .874-.855 .854-.835 .834-.815 Monastic community of Mount Athos This is a list of the administrative regions of Greece by Human Development Index as of 2023 with data for the year 2021.[1] Rank Province HDI (2021) Very high human development 1 Attica 0.909 – Greece (average) 0.887 2 Western Macedonia 0.877 3 Ionian Islands 0.876 Epirus Crete 6 Central Macedonia 0.873 Thessaly 8 North Aegean 0.865 Peloponnese So...
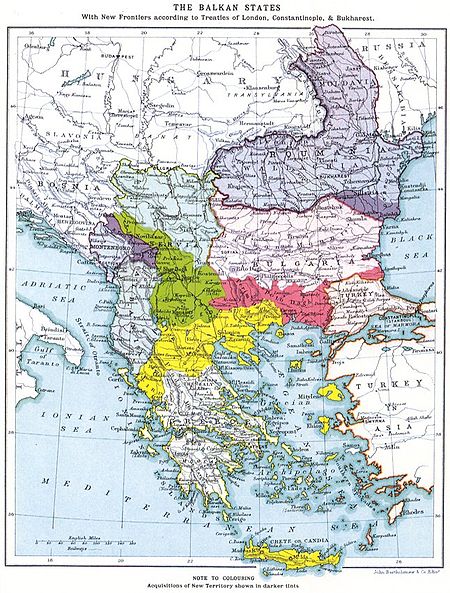
Andra Balkankriget Del av Balkankrigen Stormakterna i skräck för en explosion på Balkan. Förutom den brittiska skulle ingen stormakts tron överleva resultatet av nästa kris på Balkan 1914, som antände första världskriget. Ägde rum 16 juni 1913 – 18 juli 1913 Plats Balkanhalvön Resultat Dödläge Bulgarien efterlyser vapenvila Upphörde när Rumänien accepterade vapenvilan som ledde till Bukarestfördraget, 1913 Båda sidor hävdar seger Stridande Bulgarien Serbien Rumäni...

Muncie redirects here. For other uses, see Muncie (disambiguation). City in Indiana, United StatesMuncieCityClockwise from top: Walnut Street Historic District, Appeal to the Great Spirit, Minnetrista Museum & Gardens, Ball State University SealNickname: Middletown[1]Location of Muncie in Delaware County, IndianaMuncieShow map of IndianaMuncieShow map of the United StatesCoordinates: 40°11′48″N 85°22′30″W / 40.19667°N 85.37500°W / 40.19667;...

Christianity-related events during the 9th century See also: Christianity in the 8th century and Christianity in the 10th century For broader coverage of this topic, see Christianity of the Middle Ages. Brothers Cyril and Methodius bring Christianity to the Slavic peoples.This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (December 2022) In the 9th ce...

Hospital General de Villarrobledo LocalizaciónPaís EspañaLocalidad Avda. Miguel de Cervantes(esq. Crta. de El Provencio) s/nVillarrobledo (Albacete) España EspañaCoordenadas 39°16′48″N 2°36′09″O / 39.27996389, -2.60246111Datos generalesFundación 2007Universidad SESCAMCamas 132 110 de Hospitalización 22 de Cuidados EspecialesEspecialidad Ver especialidadesWeb oficial[editar datos en Wikidata] El Hospital General de Villarrobledo es un centr...

درآيسبآخ شعار الإحداثيات 50°37′00″N 7°55′54″E / 50.616666666667°N 7.9316666666667°E / 50.616666666667; 7.9316666666667 [1] تقسيم إداري البلد ألمانيا[2][3] التقسيم الأعلى باد مارينبيرغ خصائص جغرافية المساحة 4.62 كيلومتر مربع (31 ديسمبر 2017)[4][5] ارتفا�...

Shopping mall in Delaware, United StatesDover MallDover Mall entrance near Boscov'sLocationDover, Delaware, United StatesCoordinates39°11′39″N 75°32′23″W / 39.1942°N 75.5398°W / 39.1942; -75.5398Address1365 North Dupont Highway Ste. 5061Opening date1982ManagementSimon Property GroupOwnerSimon Property Group (68.1%)No. of stores and services79[1]No. of anchor tenants7 (5 open, 2 vacant)Total retail floor area927,414 square feet (86,160 m2)[2...

索娜姆·马利克出生2002年4月15日 (22歲)索尼帕特縣 職業业余摔跤手 索娜姆·马利克(Sonam Malik,2002年4月15日—),印度女子摔跤运动员,2023年亚洲摔跤锦标赛女子自由式62公斤级铜牌得主、2022年亚洲运动会女子自由式62公斤级铜牌得主。[1] 参考资料 ^ International Wrestling Database. [2023-10-13]. (原始内容存档于2023-10-16).

خان خانية جغتاي جغتاي خان (بالمنغولية: ᠴᠠᠭᠠᠲᠠᠢ) تمثال جغتاي خان في منغوليا خان خانية جغتاي فترة الحكم1226 – 1241-42 جنكيز خان قره هولاكو [لغات أخرى] معلومات شخصية الميلاد 22 ديسمبر 1183(1183-12-22)منغوليا الوفاة 1 جولاي 1242 (عن عمر 59)المالق، شينجيانغ الديانة التنغرية...







