Square root of 6
| |||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini memberikan informasi dasar tentang topik kesehatan. Informasi dalam artikel ini hanya boleh digunakan untuk penjelasan ilmiah; bukan untuk diagnosis diri dan tidak dapat menggantikan diagnosis medis. Wikipedia tidak memberikan konsultasi medis. Jika Anda perlu bantuan atau hendak berobat, berkonsultasilah dengan tenaga kesehatan profesional. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahka...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Ilya S...

Indian Television show This article is about Indian series. For international franchise broadcast in a number of countries, see Rising Star (TV series). Season of television series Rising StarSeason 1Country of originIndiaNo. of episodes24ReleaseOriginal networkColors TVOriginal release4 February (2017-02-04) –23 April 2017 (2017-04-23)Season chronologyNext →Season 2 Rising Star is an Indian version of the international franchise series Rising Star, a reality televisio...

Bonn Pemandangan Kota Bonn BenderaLambang kebesaranBonn di North Rhine-Westphalia Bonn Tampilkan peta JermanBonn Tampilkan peta Nordrhein-WestfalenKoordinat: 50°44′N 7°6′E / 50.733°N 7.100°E / 50.733; 7.100Koordinat: 50°44′N 7°6′E / 50.733°N 7.100°E / 50.733; 7.100NegaraJermanNegara bagianNordrhein-WestfalenWilayahKöln KreisDistrik perkotaanDidirikanabad pertama SMPemerintahan • Lord MayorAshok-Alexander Sridharan (C...
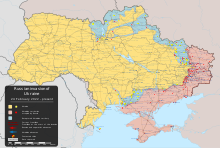
Administrasi militer-sipil LuhanskЛуганск военно-гражданская администрацияcode: ru is deprecated (Rusia)2022 Bendera Lambang Peta Administrasi Sipil Militer Luhansk, termasuk hampir seluruh Oblast LuhanskStatusDiduduki oleh RusiaIbu kotaLuhanskPemerintahan• Komandan Militer Leonid Pasechnik• Perdana Menteri Sergey Kozlov Sejarah • Pertempuran Luhansk 27 April 2014 Luas - Total8,377 km2Populasi - Perkiraan...

العلاقات الكورية الجنوبية الموزمبيقية كوريا الجنوبية موزمبيق كوريا الجنوبية موزمبيق تعديل مصدري - تعديل العلاقات الكورية الجنوبية الموزمبيقية هي العلاقات الثنائية التي تجمع بين كوريا الجنوبية وموزمبيق.[1][2][3][4][5] مقارنة بين البلدين ...

Saint-Nizier-du-Moucherotte 1. L'église Saint-Nizier et son cimetière2. L'Hôtel de ville de Saint-Nizier3. Le site de l'église, le cimetière et les Trois Pucelles4. La nécropole de Saint-Nizier et le Moucherotte Administration Pays France Région Auvergne-Rhône-Alpes Département Isère Arrondissement Grenoble Intercommunalité Communauté de communes du massif du Vercors Maire Mandat Franck Girard-Carrabin (SE) 2020-2026 Code postal 38250 Code commune 38433 Démographie Gentilé Sain...

Arifureta: From Commonplace to World's StrongestGambar sampul novel ringan volume pertama menampilkan Yueありふれた職業で世界最強(Arifureta Shokugyō de Sekai Saikyō)GenreFantasi, harem, isekai[1] Seri novelPengarangRyo ShirakomePenerbitShōsetsuka ni Narō (Penerbitan sendiri)Terbit7 November 2013 – sekarangVolume10 + 4 cerita sampingan Novel ringanPengarangRyo ShirakomeIlustratorTakayakiPenerbitOverlapPenerbit bahasa InggrisNA J-Novel Club (digital)Seven Seas (cetak)I...

Bristol Motor Speedway, salah satu sirkuit oval terkenal di Amerika Serikat. Balap lintasan oval atau balap trek oval adalah sebuah bentuk balap mobil dalam sirkuit tertutup yang diperlombakan pada sirkuit atau trek berbentuk oval. Lintasan oval berbeda dengan lintasan jalan karena tata ruangnya menyerupai oval dengan arah belokan hanya dalam satu arah yang hampir secara universal berlawanan arah jarum jam dan berbelok ke kiri. Trek oval adalah sirkuit yang benar-benar khusus untuk olahraga b...

American actress and film director (born 1962) For other people named Rebecca Miller, see Rebecca Miller (disambiguation). Rebecca MillerMiller at the 2023 BerlinaleBornRebecca Augusta Miller (1962-09-15) September 15, 1962 (age 61)Roxbury, Connecticut, U.S.OccupationScreenwriter, director, novelistAlma materYale UniversityYears active1988–presentSpouse Daniel Day-Lewis (m. 1996)Children2ParentsArthur MillerInge MorathRelativesJoan Copeland (aun...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Macedonian footballer Dragan Stojkov Dragan Stojkov playing for Saint Louis FCPersonal informationDate of birth (1988-02-23) 23 February 1988 (age 36)Place of birth Strumica, SR MacedoniaHeight 1.75 m (5 ft 9 in)Position(s) MidfielderTeam informationCurrent team AP BreraNumber 8Senior career*Years Team Apps (Gls)2005-2007 Belasica 35 (3)2007 → Incheon United (loan) 0 (0)2008 Egaleo 22 (2)2008–2010 Ilisiakos 14 (0)2009–2010 → Napredak Kruševac (loan) 19 (0)2010–2...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Jobes Milling CompanyCompany typeflour millIndustrymanufacturingPredecessorRose City Flour MillFoundedSt. Johns, Oregon, United States 1904FounderWilliam Van Zant JobesDefunct1930Fatesold 1918; demolished 1930HeadquartersSt. Johns, Oregon (1904–15)Portland, Oregon (1915–30)Key peopleAllan R. and William Haskell JobesOwnerWilliam Van Zant Jobes (1904–07)Allan R. and William Haskell Jobes (1907–11)Allan R. Jobes (1911–18)Rose City Flour Mill (1918–30)ParentRose City Flour Mill (1918...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Meihuaquan – news · newspapers · books · scholar · JSTOR (September 2015) (Learn how and when to remove thi...

سيفيرينيا زيمليا الإحداثيات 79°45′N 98°15′E / 79.75°N 98.25°E / 79.75; 98.25 سبب التسمية نيقولا الثاني إمبراطور روسيا تقسيم إداري البلد روسيا[1] التقسيم الأعلى كراسنويارسك كراي خصائص جغرافية المساحة 37000 كيلومتر مربع ارتفاع 965 متر عدد الس...

Thomas Croft NeibaurPenerima Medal of HonorLahir(1898-05-17)17 Mei 1898Sharon, IdahoMeninggal23 Desember 1942(1942-12-23) (umur 44)Walla Walla, WashingtonTempat pemakamanSugar City, IdahoPengabdianAmerika SerikatDinas/cabangAngkatan Darat Amerika SerikatLama dinas1917 - 1919PangkatPrivatKesatuanResimen Infanteri ke-167, Divisi Infanteri ke-42Perang/pertempuranPerang Dunia IPenghargaanAmerika Serikat:Medal of HonorPurple HeartWorld War I Victory MedalPrancis:Légion d'honneur - Cheva...

Team sport This article is about the indoor team sport. For the beach team sport, see Beach volleyball. For other uses, see Volleyball (disambiguation). See also: Throwball and Newcomb ball This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Volleyball – news · newspapers · books · scholar · JSTOR (September 201...

American businessman and politician For the New Zealand mayor, see Will Appleton. William AppletonMember of theU.S. House of Representatives from MassachusettsIn officeMarch 4, 1851 – March 3, 1855Preceded bySamuel Atkins EliotSucceeded byAnson BurlingameConstituency1st district (1851–53)5th district (1853–55)In officeMarch 4, 1861 – September 27, 1861Preceded byAnson BurlingameSucceeded bySamuel HooperConstituency5th district Personal detailsBorn(1786-11-16)November...






![{\displaystyle [2;2,4,2,4,2,\ldots ]=2+{\cfrac {1}{2+{\cfrac {1}{4+{\cfrac {1}{2+{\cfrac {1}{4+\dots }}}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7ea5ff4f26c9c2429cfdd0375c5a1e349b65209)




























