Algebraic integer
|
Read other articles:

In association football, or soccer, scoring a goal is the only method of scoring. In National Collegiate Athletic Association (NCAA) Division I soccer, where a player's career is at most four seasons long, it is considered a notable achievement to reach the 60-goal threshold. In even rarer instances, players have reached the 80 and 100-goal plateaus. The top 30 highest goal-scorers in NCAA Division I men's soccer history are listed below. The NCAA did not split into its current divisions for...

Sungai JubbaPeta aliran lembah sungai Jubba/ShebelleLokasiNegaraSomaliaEtiopiaCiri-ciri fisikHulu sungai - lokasiPertemuan Sungai Dawa dan Sungai Ganale Dorya - koordinat4°10′38″N 42°04′51″E / 4.1771°N 42.0809°E / 4.1771; 42.0809 Muara sungai - lokasiLaut Somali - koordinat0°14′58″S 42°37′51″E / 0.2495°S 42.6307°E / -0.2495; 42.6307Koordinat: 0°14′58″S 42°37′51�...

Wind farm off Peterhead, Scotland Hywind ScotlandCountryScotland, United KingdomLocationScotland, GrampianCoordinates57°28′59″N 1°21′00″W / 57.483°N 1.35°W / 57.483; -1.35StatusOperationalConstruction began2016Commission dateOctober 2017Construction cost£264mOwner(s)Equinor (75%)Masdar (25%)Operator(s)Hywind (Scotland) LimitedWind farm TypeOffshoreMax. water depth95–120 m (312–394 ft)Distance from shore...

Soviet ultraviolet space telescope AstronMission typeAstrophysical researchOperatorUSSRCOSPAR ID1983-020A [1]SATCAT no.13901Mission duration8 years Start of missionLaunch date23 March 1983 12:45 (1983-03-23UTC12:45) UTCRocketProton-K/D-1 8K82K/11S824MLaunch siteTYURATAM MISSILE AND SPACE COMPLEX End of missionDisposalDecommissionedDeactivatedMarch 23, 1991 Orbital parametersReference systemGeocentricRegimeHigh EarthSemi-major axis108,531 km (67,438 mi) ...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Overview of music traditions in Germany German song redirects here. For the No Money Enterprise song, see German (song). Music of Germany General topics German composers Genres Church music Classical Electronic Heavy metal Thrash metal Highlife Electronic music Hip hop Jazz Medieval metal Neue Deutsche Welle Opera Punk Rock (Neue Deutsche Härte, Krautrock, Ostrock) Schlager Volkslied Volksmusik Volkstümliche Musik Specific forms Guggenmusik Lied Schuhplattler Yodeling Media and performance ...

British band This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bill Wyman's Rhythm Kings – news · newspapers · books · scholar · JSTOR (March 2012) (Learn how and when to remove this message) Bill Wyman's Rhythm KingsBill Wyman's Rhythm Kings Middelburg January, 2009Background informationOriginLondon, EnglandG...
الكامل في ضعفاء الرجال الكامل في ضعفاء الرجال معلومات الكتاب المؤلف ابن عدي(277 هـ - 365 هـ) البلد جرجان اللغة العربية الناشر دار الكتب العلمية، دار الفكر، مكتبة الرشد السلسلة كتب الرجال الموضوع علم التراجم - علم الرجال الفريق فنان الغلاف الغلاف الداخلي لكتاب الكامل في ضعفاء �...

2012年夏季奥林匹克运动会几内亚比绍代表團几内亚比绍国旗IOC編碼GBSNOC幾內亞比索奧林匹克委員會網站cogb.gw(葡萄牙文)2012年夏季奥林匹克运动会(倫敦)2012年7月27日至8月12日運動員4參賽項目2个大项旗手奧古斯托·米達納历届奥林匹克运动会参赛记录(总结)夏季奥林匹克运动会19962000200420082012201620202024 2012年夏季奥林匹克运动会畿內亞比紹代表团參加2012年7月27日至8月12...
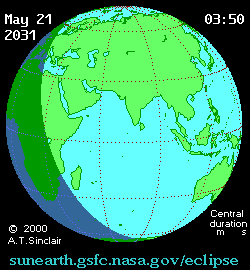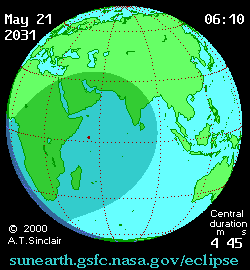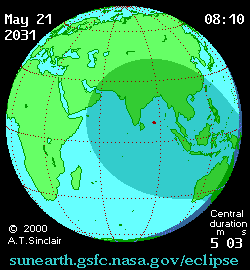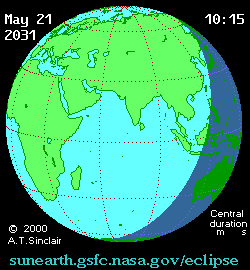
Future annular solar eclipse Solar eclipse of May 21, 2031MapType of eclipseNatureAnnularGamma−0.197Magnitude0.9589Maximum eclipseDuration326 s (5 min 26 s)Coordinates8°54′N 71°42′E / 8.9°N 71.7°E / 8.9; 71.7Max. width of band152 km (94 mi)Times (UTC)Greatest eclipse7:16:04ReferencesSaros138 (32 of 70)Catalog # (SE5000)9577 An annular solar eclipse will occur at the Moon's descending node of orbit on Wednesday, May 21, 2031,...

ロタール2世Lothar II ロタリンギア国王 在位 855年 - 869年出生 835年死去 869年8月8日ピアチェンツァ埋葬 ピアチェンツァ、サンタントニーノ聖堂配偶者 テウトベルガ子女 一覧参照(庶子のみ)家名 カロリング家王朝 カロリング朝父親 ロタール1世母親 エルマンガルド・ド・トゥール宗教 カトリック教会テンプレートを表示 ロタール2世(Lothar II, 835年 - 869年8月8日)は、中...

La guerre des Boers (prononcé aujourd'hui « bour » la plupart du temps, proche de la prononciation néerlandaise et afrikaans, mais à l'époque en France on écrivait aussi Boërs, avec la prononciation en rapport) est une expression qui désigne deux conflits intervenus en Afrique du Sud à la fin du XIXe siècle entre les Britanniques et les habitants des deux républiques boers indépendantes : la première guerre des Boers : du 16 décembre 1880 au 23 mars 188...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2020) جيسي فيسل معلومات شخصية الميلاد 13 أبريل 1894 تاريخ الوفاة 23 أغسطس 1948 (54 سنة) مواطنة السويد الحياة العملية المهنة ممثلة المواقع IMDB صفحتها على IM...

Bạn có thể mở rộng bài này bằng cách dịch bài viết tương ứng từ ngôn ngữ khác. (tháng 2/2022) Nhấn [hiện] để xem các hướng dẫn dịch thuật. Đừng dịch những nội dung không đáng tin hay chất lượng thấp. Nếu được, bạn hãy tự kiểm chứng các thông tin bằng các nguồn tham khảo có trong bài gốc. Bạn phải ghi công bản quyền bài gốc trong tóm lược sửa đổi bài dịch. Chẳng hạn, b...

日本通信TiKiモバイル BM-SW キャリア 日本通信TiKiモバイル 製造 華為技術 発売日 2010年12月25日 概要 OS Android 2.2.1 Froyo CPU Qualcomm MSM7225 528MHz 音声通信方式 FOMA(W-CDMA)GSM(850/1700/1900/2100MHz(W-CDMA)850/900/1800/1900MHz(GSM)) データ通信方式 HSDPAGPRSEDGEIEEE 802.11b/g/n(Wi-Fi) 形状 ストレート・タッチパネル サイズ 54.8×104×13.5mm 質量 約100 g 連続通話時間 9時間 連続待受時間 288時間 外部メ�...

Part of a series onChemistryScience of matter Index Outline Glossary History (timeline) Key components Matter Phase Bond Chemical reaction Ion Acid–base reaction Redox Chemical equilibrium Chemical law Branches Analytical chemistry Biochemistry Organic chemistry Inorganic chemistry Physical chemistry Research Chemist (list) List of chemistry awards List of journals List of unsolved problems Chemistry portal Categoryvte An image from John Dalton's A New System of Chemical Philosop...

This article is about the United Kingdom body. For the Canadian body, see Chiefs of Staff Committee (Canada). Committee of the professional heads of the United Kingdom's armed forces The Tri-Service Badge of the British Armed Forces The Chiefs of Staff Committee (CSC) is composed of the most senior military personnel in the British Armed Forces who advise on operational military matters and the preparation and conduct of military operations. The committee consists of the Chief of the Defence ...

Problem in mathematical optimisation In mathematical optimization, Zermelo's navigation problem, proposed in 1931 by Ernst Zermelo, is a classic optimal control problem that deals with a boat navigating on a body of water, originating from a point A {\displaystyle A} to a destination point B {\displaystyle B} . The boat is capable of a certain maximum speed, and the goal is to derive the best possible control to reach B {\displaystyle B} in the least possible time. Zermelo Navigation with vel...

Pour les articles homonymes, voir Pont (toponyme) et Mousson (homonymie). Pont-à-Mousson De haut en bas, de gauche à droite : la Moselle et l'abbaye des Prémontrés ; l'église Saint-Laurent ; l'église Saint-Martin ; la maison des Sept-Péchés-capitaux ; l'hôtel de ville ; l'abbaye des Prémontrés et alentours. Blason Logo Administration Pays France Région Grand Est Département Meurthe-et-Moselle Arrondissement Nancy Intercommunalité Communauté de com...

Russian author and revolutionary (1812–1870) Alexander HerzenPortrait of Herzen by Nikolai Ge (1867)BornAleksandr Ivanovich Herzen6 April 1812 (1812-04-06)Moscow, Moskovsky Uyezd, Moscow Governorate, Russian EmpireDied21 January 1870 (1870-01-22) (aged 57)Paris, FranceAlma materMoscow UniversityEra19th-century philosophyRegionRussian philosophySchoolWesternizersAgrarian populismMain interestsPolitics, economics, class struggleNotable ideasAgrarianism Signature Alexander ...

![{\displaystyle \mathbb {Z} [\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28420682be585a0ee588c7eb13e7971e01cb1283)



![{\displaystyle f(x)\in \mathbb {Z} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb8266c32dfc2904dc4331ea8906ad341a05ce1c)
![{\displaystyle \mathbb {Z} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d4da3ac703cc7721ebba91a53f6752de7157124)






![{\displaystyle F=\mathbb {Q} [\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18fe97465addcc1c7d3f2a3a68e369894145b652)


![{\displaystyle \mathbb {Z} [\zeta _{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77d56918ae77f0c6d51f8404ce9240aacca9780e)


