انحراف معياري
|
Read other articles:
Rasio bendera: 3:5 Bendera Palau disetujui tanggal 1 Januari 1981. Ketika kumpulan pulau ini berpisah dari Teritori Perjanjian Perserikatan Bangsa-Bangsa, Palau menggunakan bendera ini. Sama dengan kumpulan pulau Pasifik lainnya, biru adalah warna yang digunakan untuk menggambarkan lautan dan letak negara di sana. Sementara bendera ini menyamakan Palau dengan Persatuan Negara Mikronesia dan kumpulan pulau tetangganya, bulatan pada bendera itu sama dengan bendera Bangladesh (juga bendera Jepa...

This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) This list is incomplete; you can help by adding missing items. (January 2012) This...
Liga Negara UEFAMulai digelar2018WilayahEropa (UEFA)Jumlah tim55Kualifikasi untukKejuaraan Eropa UEFAJuara bertahan Spanyol (gelar ke-1)Tim tersukses Prancis Portugal Spanyol (masing-masing 1 gelar)Situs webSitus web resmi Liga Negara UEFA 2024–2025 Liga Negara UEFA (Inggris: UEFA Nations Leaguecode: en is deprecated ) adalah sebuah kompetisi sepak bola yang mempertandingkan tim nasional senior dari negara-negara anggota UEFA, badan pengatur sepak bola Eropa.[1] ...

Banfield 2019–20 football seasonBanfield2019–20 seasonPresidentLucía BarbutoManagerHernán Crespo(until 2 September 2019)Julio César Falcioni(from 5 September 2019)StadiumEstadio Florencio SolaTop goalscorerLeague: Nicolás Bertolo (1)Sergio VittorAgustín FontanaAll: Nicolás Bertolo (1)Sergio VittorAgustín Fontana← 2018–192020–21 → The 2019–20 season is Banfield's 7th consecutive season in the top division of Argentine football.[1] In addition to ...

Cheval androcéphale ailé (à droite) sur un statère en or des Cénomans. Le cheval androcéphale est un motif de cheval à tête humaine et attributs masculins, présent sur de nombreuses pièces de monnaie celtiques de l'Antiquité frappées par des peuples celtes établis sur la façade atlantique, surtout en Armorique. Ce motif est présent sur les monnaies des Vénètes, des Aulerques Cénomans et des Trévires. Il orne également un couvercle de cruche retrouvé à Reinheim dans l'oue...
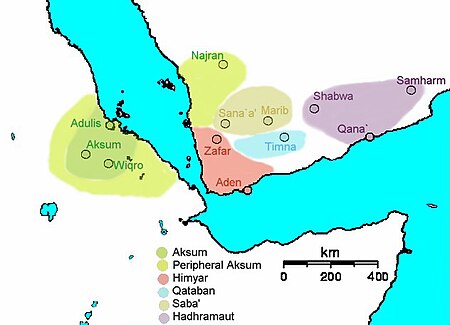
Voci principali: Storia dell'antico Yemen, Regno di Saba. Regno di Sheba (senape) nel III secolo d.C. I Sabei (in arabo السَّبَئِيون/السَّبأيون?, al-Saba’iyyūn/al-Sabā'yyūn, o in ebraico סבאים?, Saba'im) furono un antico popolo parlante una lingua sudarabica, fiorito nel II millennio a.C. nel sud della penisola Arabica (attuale Yemen). Il loro regno di Saba (in arabo سَبأ?, Sabāʾ, e (in ebraico סבא?, Sab...

جون ريجنالد ريتشاردسون معلومات شخصية الميلاد سنة 1912إدمونتون الوفاة 25 نوفمبر 1997 (84–85 سنة)فريمونت مواطنة كندا الحياة العملية المدرسة الأم جامعة كاليفورنياجامعة كاليفورنيا، بركلي مشرف الدكتوراه إرنست أورلاندو لورنس المهنة فيزيائي اللغات الإ�...

Pour les articles homonymes, voir Grec et grc. Grec ancienἙλληνική Période IXe siècle av. J.-C. – VIe siècle apr. J.-C. Langues filles Grec de la koinè Région Méditerranée orientale Typologie SOV, SVO[1], flexionnelle, accusative, à accent de hauteur Classification par famille - langues indo-européennes - langues helléniques - grec ancien Codes de langue IETF grc ISO 639-2 grc ISO 639-3 grc Étendue Langue individuelle Type Langue historique Glottolog anci...

Ernest ReyerPortrait photographique de Reyer par Carjat.BiographieNaissance 1er décembre 1823MarseilleDécès 15 janvier 1909 (à 85 ans)Le LavandouSépulture Cimetière Saint-Pierre de MarseilleNom de naissance Louis Étienne Ernest ReyNationalité françaiseFormation Lycée ThiersConservatoire à rayonnement régional de MarseilleActivités Compositeur, critique musicalParentèle Louise Farrenc (tante)Aristide Farrenc (oncle)Autres informationsMembre de Académie des beaux-a...

Questa voce o sezione sugli argomenti storia economica e economia internazionale non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Il sistema aureo è un sistema monetario nel quale la base monetaria è data da una quantità fissata d'oro. Indice 1 Descrizione 1.1 Vantaggi 1.2 Svantaggi 2 Storia 2.1 Il sistema gold standard 2.2 Le principali monete nel gol...

JamaikaJulukanThe ReggaeboyzAsosiasiFederasi Sepak Bola Jamaika (JFF)KonfederasiCONCACAF (Amerika Utara, Tengah, dan Karibia)Sub-konfederasiCFU (Karibia)Pelatih Heimir HallgrímssonKaptenAndre BlakePenampilan terbanyakIan Goodison (128)[1]Pencetak gol terbanyakLuton Shelton (35)Stadion kandangIndependence ParkKode FIFAJAMPeringkat FIFATerkini 55 2 (4 April 2024)[2]Tertinggi27 (Agustus 1998)Terendah116 (Oktober 2008)Peringkat EloTerkini 56 12 (19 Januari 2024)[3] Warna ...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Closed railway station in City of Edinburgh, Scotland, UK JoppaRemains of the former Joppa station building.General informationLocationJoppa, EdinburghScotlandCoordinates55°56′50″N 3°06′06″W / 55.9472°N 3.1016°W / 55.9472; -3.1016Grid referenceNT313732Platforms2Other informationStatusDisusedHistoryOriginal companyNorth British RailwayPre-groupingNorth British RailwayPost-groupingLondon and North Eastern RailwayKey dates16 May 1859 (1859-05-16...

Belgian footballer Jean Thissen Thissen in 1968Personal informationDate of birth (1946-04-21) 21 April 1946 (age 78)Place of birth Ensival, BelgiumPosition(s) DefenderSenior career*Years Team Apps (Gls)1965–1974 Standard Liège 1974–1979 Anderlecht International career1968–1977 Belgium 34 (0)Managerial career1988–1990 Beira-Mar1991 Servette1992 Union Saint-Gilloise1992–1994 Gabon1994–1995 Raja Casablanca1996–1998 Stade Tunisien2000 Standard Liège2004–2005 Virton2007–20...
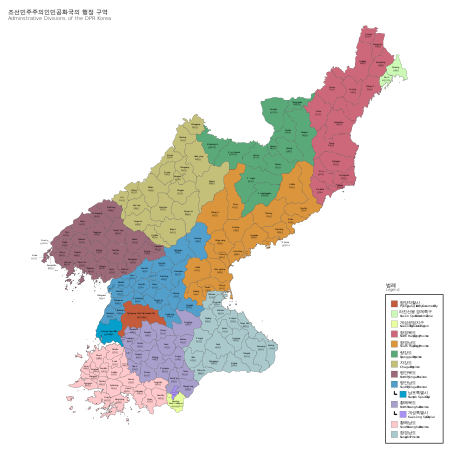
Overview of the administrative divisions of North Korea This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (September 2016) (Learn how and when to remove this message) This article is part of a series on theAdministrative divisions of North Korea Provincial level Province(도 道 to) Special municipality(특별시 特別市 t'ŭ...
Map Tamaudun (玉陵) is one of the three royal mausoleums of the Ryukyu Kingdom, along with Urasoe yōdore at Urasoe Castle and Izena Tamaudun near Izena Castle in Izena, Okinawa. The mausoleum is located in Shuri, Okinawa, and was built for Ryūkyūan royalty in 1501[1] by King Shō Shin, the third king of the Second Shō Dynasty a short distance from Shuri Castle. Overview The site, covering an area of 2,442 m2,[2] consists of two stone-walled enclosures, the three com...

注意:本页有Unihan扩展B区汉字:「𤩝」,這些字符可能會错误显示,詳见Unicode扩展汉字。 Cuqicuq Garuljigulj斯卡羅酋邦頭目臺灣統治者石門戰役後,日軍指揮官西鄉從道與排灣族領袖合影。左坐者為卓杞篤之養子朱雷,中坐者為西鄉、右坐者為亦失。斯卡羅酋邦頭目統治約十九世紀加冕約十九世紀中前任Paljaljaus繼任朱雷安葬豬朥束社配偶Qisi子嗣養子朱雷 養子文杰王朝卡�...

Name of several individuals in Greek mythology There are several characters named Acmon or Akmon (Ancient Greek: Ἄκμων means 'anvil, pestle'[1]) in Greek mythology: Acmon, one of the mythical race of Dactyls.[2] Acmon, a Phrygian king who gave his name to the district known as Acmonia.[3] Acmon, a mischievous forest creature who lived in Thermopylae or on Euboea but roamed the world and might turn up anywhere mischief was afoot.[4] Acmon, a companion of D...

Questa voce o sezione sull'argomento sport non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. UltimateUna fase dell'incontro tra Canada e Gran Bretagna nel corso dei Giochi mondiali di Kaohsiung 2009FederazioneWorld Flying Disc Federation Componenti di una squadra7 ContattoVietato Genereopen, femminile e mix...

Strukturformel Keile zur Verdeutlichung der räumlichen Struktur Allgemeines Name Wasserstoffperoxid Andere Namen Perhydrol Wasserstoffsuperoxid Hydrogenium peroxydatum Dioxidan HYDROGEN PEROXIDE (INCI)[1] Summenformel H2O2 Kurzbeschreibung farblose, fast geruchlose Flüssigkeit[2] Externe Identifikatoren/Datenbanken CAS-Nummer 7722-84-1 (wässrige Lösung) EG-Nummer 231-765-0 ECHA-InfoCard 100.028.878 PubChem 784 DrugBank DB11091 Wikidata Q171877 Arzneistoffangaben ATC-Code ...





















