انحدار خطي
|
Read other articles:

You can help expand this article with text translated from the corresponding article in French. (May 2023) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unreliable or low-qua...

AmletoL'apparizione dello spirito del vecchio re, vittima di omicidio e padre del protagonista AmletoTitolo originaleHamlet Paese di produzioneRegno Unito Anno1948 Durata155 min Dati tecniciB/N Generedrammatico RegiaLaurence Olivier SoggettoWilliam Shakespeare SceneggiaturaLaurence Olivier, Reginald Beck e Anthony Bushell ProduttoreLaurence Olivier Casa di produzioneTwo Cities Films FotografiaDesmond Dickinson MontaggioHelga Cranston MusicheWilliam Walton ScenografiaRoger K. Furse CostumiRoge...

Vous lisez un « bon article » labellisé en 2017. Pour les articles homonymes, voir Evers. Medgar EversMedgar Evers à la Maison-Blanche en 1961.BiographieNaissance 2 juillet 1925DecaturDécès 12 juin 1963 (à 37 ans)JacksonSépulture Cimetière national d'Arlington (19 juin 1963)Nationalité américaineFormation Université d'État AlcornActivités Homme politique, militant pour les droits de la personne humaineFratrie Charles EversConjoint Myrlie Evers-Williams (de 1951 �...

American food reality television series Food Network StarGenreFood reality televisionJudges Marc Summers Bobby Flay Giada De Laurentiis Alton Brown Country of originUnited StatesNo. of seasons14No. of episodes75ProductionProduction locationsNew York City and Burbank, CaliforniaRunning time40–120 minutesProduction companiesCBS EYEtoo Productions (Seasons 1-8)Triage Entertainment (Seasons 9-14)Original releaseNetworkFood NetworkReleaseJune 5, 2005 (2005-06-05) –August 5, 2018 ...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Франц Саксен-Кобург-Заальфельдскийнем. Franz von Sachsen-Coburg-Saalfeld герцог Саксен-Кобург-Заальфельдский 8 сентября 1800 — 9 декабря 1806 Предшественник Эрнст Фридрих Саксен-Кобург-Заальфельдский Преемник Эрнст I Саксен-Кобург-Заальфельдский Рождение 15 июля 1750(1750-07-15)Кобург, Сакс...
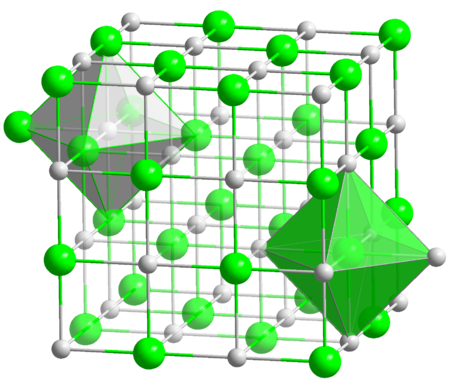
Plutonium nitride Names Other names plutonium mononitride, azanylidyneplutonium, plutonium(III) nitride Identifiers CAS Number 12033-54-4 Y 3D model (JSmol) Interactive image InChI InChI=1S/N.PuKey: DPJMGCIEQAVKAI-UHFFFAOYSA-N SMILES [N].[Pu] Properties Chemical formula NPu Molar mass 258 g·mol−1 Appearance Grey crystalline solid Density 14.2 g/cm3 Melting point 2,589 °C (4,692 °F; 2,862 K) Solubility in water insoluble Except where otherwise noted, ...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...
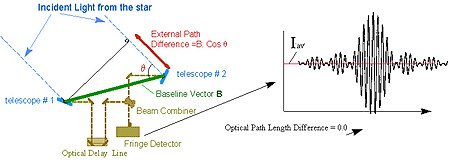
Astrometri interferometri Astrometri adalah cabang dari astronomi yang memusatkan perhatian pada posisi bintang dan benda langit lainnya, jarak dan pergerakan mereka. Sebagian astrometri melibatkan pembuatan tangga jarak kosmik. Astrometri adalah salah satu sub-bidang ilmu yang paling tua, kembali ke zaman Hipparchus, yang menyusun katalog bintang yang pertama. Hipparchus juga menciptakan skala kecerahan yang masih dipergunakan sampai sekarang. Astrometri modern dirintis oleh Friedrich Bessel...

South African-American filmmaker (born 1986) Melissa Cohen BidenBiden in 2021BornMelissa Batya Cohenc. 1986 (age 37–38)Johannesburg, South AfricaEducationGreenside Design Center College of DesignUniversity of California, Los AngelesOccupation(s)Activist, filmmakerSpouse Jason Lavender (m. 2011; div. 2014) Hunter Biden (m. 2019)Children1FamilyBiden (by marriage) Melissa Batya Cohen Biden (born c. 1...

American basketball player and coach This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Cliff Hagan – news · newspapers · books · scholar · JSTOR (June 2021) (Learn how and when to remove this mess...

Una presumibile scala della piacevolezza degli odori secondo l'uomo L'odore è un'esperienza sensoriale, causata da uno o più composti chimici volatilizzati anche ad una concentrazione molto bassa, che gli esseri umani o altri animali percepiscono con il senso dell'olfatto. L'odore è un'emanazione trasmessa principalmente dall'aria percepita dall'apparato olfattivo dell'uomo e degli animali in generale, e che può fungere da stimolo, conscio o inconscio, per richiamare ricordi, emozioni, bi...

Radio station facility Radio tower and mast Radio mast The Richtfunkstelle Berlin-Frohnau (Directional radio station Berlin-Frohnau) was a facility for directional radio services in Frohnau (a locality in the Reinickendorf borough of Berlin; during the Cold War, the northernmost locality of West Berlin). Before German reunification, the facility served as a microwave transmission link between West Berlin and West Germany. It first used only an overhorizon directional link. For this link betwe...

Seven-a-side ball sport NetballMalawi (red) playing Fiji (blue)at the 2006 Commonwealth GamesHighest governing bodyWorld NetballFirst played1897; 127 years ago (1897),[1] England, United KingdomRegistered players561,000+[n 1]CharacteristicsContactLimitedTeam membersSeven on-court players per team All-female teams All-male teams Mixed teams Type Team sport Ball sport EquipmentNetball, bibVenueNetball courtPresenceOlympicIOC-recognised federation, 1995[...

Cross enclosed in a ring or halo This article is about the Christian symbolism. For the wider concept, see Sun cross. The ringed cross is a class of Christian cross symbols featuring a ring or nimbus. The concept exists in many variants and dates to early in the history of Christianity. One variant, the cruciform halo, is a special type of halo placed behind the head of Jesus in Christian art. Other common variants include the Celtic cross, used in the stone high crosses of France, Ireland an...

Santiago de Murcia Jácaras are Spanish songs which are accompanied with instruments and are performed during the entr'acte of a theatrical performance and also as an accompaniment to many types of dance. Etymology There are different explanations for the origin of the term. Corominas (1954) gives the origin as an Arabic word for chess,[1] other sources give the origin as Arabic for bellowing or making someone angry.[2] Texts The form may be textless, as in the compositions of...

Disused railway line in Yorkshire, England Harrogate–Church Fenton lineProspect TunnelOverviewStatusClosed from Crimple junction to Church Fenton junctionLocaleNorth YorkshireTerminiHarrogateChurch Fenton North JunctionStations8ServiceTypeHeavy railOperator(s)York and North Midland Railway to 1854North Eastern Railway 1854–1923London and North Eastern Railway 1923–1948British Railways (N.E region) 1948 to closureDepot(s)Harrogate Low (Brunswick, closed 1862)[1]HistoryOpened10 Au...

1983 Sudanese presidential election ← 1977 14 and 25 April 1983 1996 → Nominee Jaafar Nimeiry Party SSU Percentage 99.6% President before election Jaafar Nimeiry SSU Elected President Jaafar Nimeiry SSU Politics of Sudan Member State of the Arab League Constitution 4 August 2019 Draft Constitutional Declaration Executive Presidency Transitional Sovereignty Council Chairman: Abdel Fattah al-Burhan Deputy Chairman: Malik Agar Prime Minister Osman Hussein (acting) Ca...

В Википедии есть статьи о других людях с фамилией Прайс. Том Прайс Гражданство Великобритания Дата рождения 11 июня 1949(1949-06-11) Место рождения Ритин, Денбишир, Уэльс, Великобритания Дата смерти 5 марта 1977(1977-03-05) (27 лет) Место смерти Кьялами, ЮАР Выступления в чемпионате мира Ф�...
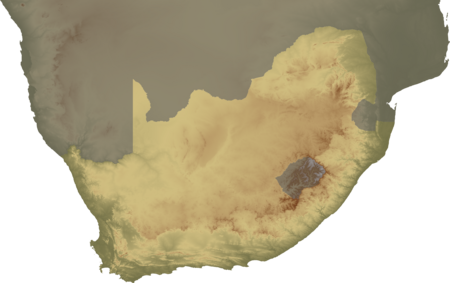
Former confederation in modern day South Africa (1780-1817) MtetwaMthethwa Paramountcyc. 1780–1817NdwandweMthethwaclass=notpageimage| Locations of the Mthethwa Paramountcy, and the rival Ndwandwe clan on a map of present-day KwaZulu-Natal, South AfricaOfficial languagesNguniGovernmentConfederationnKosi • c. 1780–1806 Jobe kaKhayi• 1806–1817 Dingiswayo History • Established c. 1780• Disestablished 1817 Preceded by Succeeded by Nguni culture Zulu...



































![{\displaystyle (i,k)\in [1,...,n]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e31d31dbfba342613b7a7a6dc00ca7e8b8a93e8)








