متغير إحصائي
|
Read other articles:

Nereo Rocco Informasi pribadiTanggal lahir (1912-05-20)20 Mei 1912Tempat lahir Trieste, Austria-HungariaTanggal meninggal 20 Februari 1979(1979-02-20) (umur 66)Tempat meninggal Trieste, ItaliaPosisi bermain Gelandang, pemain depanKarier junior1927–1930 TriestinaKarier senior*Tahun Tim Tampil (Gol)1930–1937 Triestina 232 (66)1937–1940 Napoli 52 (7)1940–1942 Padova 47 (14)1942–1943 94° Reparto Distretto Trieste – (–)1943–1944 Libertas Trieste 14 (1)1944–1945 Padova – ...

Persijap JeparaNama lengkapPersatuan Sepak bola Indonesia JeparaJulukanLaskar Kalinyamat Elang-Laut JawaBerdiri11 April 1954StadionStadion Gelora Bumi KartiniKabupaten Jepara, Provinsi Jawa Tengah(Kapasitas: 25.000)PemilikPT. Jepara Raya MultitamaPresiden Muhammad Iqbal Hidayat[1]Pelatih Alfiat [2]LigaLiga 22022Peringkat 2 Grup Tengah (Kompetisi dihentikan)Situs webSitus web resmi klubKelompok suporter Banaspati Jetman CNS (Curva Nord Syndicate) Kostum kandang Kostum tand...
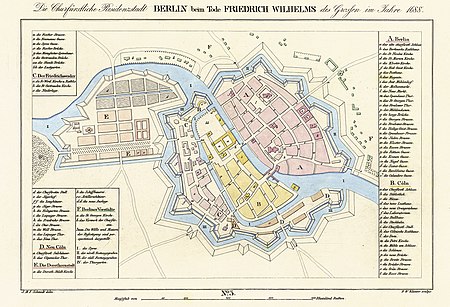
Capital and largest city of Germany This article is about the capital city of Germany. For other uses, see Berlin (disambiguation). Place in GermanyBerlinCapital city, state and municipalitySpree river, Museum Island and Berlin TV Tower in MitteVictory ColumnCharlottenburg PalaceRotes RathausBrandenburg GateReichstagBerlin CathedralPotsdam Square FlagCoat of armsNicknames: Grey City[1] Spreeathen, or Athens on the Spree River[2]Show BerlinShow EuropeCoordinates: 52°31′...

Bridge in Melbourne, AustraliaMorell BridgeCoordinates37°49′40″S 144°59′06″E / 37.8277°S 144.985°E / -37.8277; 144.985CarriesPedestrians and cyclistsCrossesYarra RiverLocaleMelbourne, AustraliaOfficial nameMorell BridgeOther name(s)Anderson Street bridgeCharacteristicsDesignArch bridgeHistoryOpened1899Location The Morell Bridge is an arch bridge over the Yarra River in South Yarra, Melbourne, Victoria, Australia. Completed in 1899 by John Monash and J. T. ...

Cupa României 1999-2000 Competizione Cupa României Sport Calcio Edizione 62ª Organizzatore FRF Date dal 21 settembre 1999al 13 maggio 2000 Luogo Romania Partecipanti 32 Risultati Vincitore Dinamo Bucarest(8º titolo) Secondo Universitatea Craiova Cronologia della competizione 1998-1999 2000-2001 Manuale La Cupa României 1999-2000 è stata la 62ª edizione della coppa nazionale disputata tra il 21 settembre 1999 e il 13 maggio 2000 e conclusa con la vittoria della Dinamo Buc...

Pelforth–Sauvage–LejeunePelforth–Sauvage–Lejeune riders Jan Janssen and Dick Enthoven at the 1963 Tour de FranceTeam informationRegisteredFranceFounded1960 (1960)Disbanded1968Discipline(s)RoadTeam name history196019611962–1968Pelforth 43–CarlierSauvage–Lejeune–Pelforth 43Pelforth–Sauvage–Lejeune Pelforth–Sauvage–Lejeune was a French professional cycling team that existed from 1960 to 1968.[1] Jan Janssen won the 1968 Tour de France with the team.[2]...

Nationalliga 1972-1973 Competizione Fußball-Bundesliga Sport Calcio Edizione 62ª Organizzatore ÖFB Luogo Austria Partecipanti 16 Cronologia della competizione 1971-72 1973-74 Manuale L'edizione 1972-73 della Nationalliga (A) vide la vittoria finale del FC Wacker Innsbruck. Capocannoniere del torneo fu Wolfgang Breuer del FC Wacker Innsbruck con 22 reti. Classifica finale Classifica G V N P GF GS Pt 1 FC Wacker Innsbruck 30 18 7 5 57 25 43 2 Rapid Vienna 30 16 8 6 50 31 40 3 Grazer A...

American football player and sports coach (1878–1948) Frank CayouCayou at Wabash, c. 1907Biographical detailsBorn(1878-03-07)March 7, 1878Decatur, Nebraska, U.S.DiedMay 7, 1948(1948-05-07) (aged 70)[1]Hominy, Oklahoma, U.S.Playing careerFootball1895–1898Carlisle1898Dickinson1899–1901IllinoisTrack and field1896–1898Carlisle1899Dickinson1900–1902Illinois Position(s)Quarterback, running backCoaching career (HC unless noted)Football1902Champaign Central HS (IL)1904–1907Wa...

Class III shortline railroad in Missouri This article is about the Missouri & Northern Arkansas Railroad (1992). It is not to be confused with the Missouri & North Arkansas Railroad (1906-1946). Missouri & Northern Arkansas RailroadMNA 3363, an EMD SD40-2 idling at Pearl Yard in Carthage, Missouri.OverviewHeadquartersCarthage, MissouriReporting markMNALocaleArkansas, Kansas, MissouriDates of operation1992–presentTechnicalTrack gauge4 ft 8+1⁄2 in (1,435&#...

This article may be unbalanced toward certain viewpoints. Please improve the article by adding information on neglected viewpoints, or discuss the issue on the talk page. (September 2023) Educational method and philosophy; form of homeschooling Children investigating insect deposits in tree bark as part of an unschooling activity Part of the Politics series onStudents' rights History 2021 Boğaziçi University protests 2021 Columbia University strike 2020 Thai protests School strike for clima...

French mathematician Pierre CartierBornPierre Émile Cartier (1932-06-10) 10 June 1932 (age 91)Sedan, ArdennesNationalityFrenchAlma materUniversity of ParisKnown forCartier divisorCartier dualityCartier isomorphismCartier operatorCartier's theoremCartier–Foata matricesTracesAwardsPrix Peccot (1960)[1]ICM Speaker (1970)Prize Ampère (1978)Scientific careerFieldsMathematicsInstitutionsUniversity of StrasbourgInstitut des Hautes Études ScientifiquesDoctoral advisorHenri...

American TV series or program George WashingtonGenreBiographyDramaHistoryWarMiniseriesBased onGeorge Washington by James Thomas FlexnerScreenplay byJon BootheRichard FielderDirected byBuzz KulikStarringBarry BostwickPatty Duke AstinTheme music composerLaurence RosenthalCountry of originUnited StatesOriginal languageEnglishNo. of episodes3ProductionProducersRichard FielderBuzz KulikDavid GerberCinematographyHarry Stradling Jr.EditorsDonald DouglasMel FriedmanLes GreenDavid WagesRunning time48...

Integrated network of highways and roads in the Republic of Turkey Devlet YoluRoute markers for three Turkish State RoadsSystem informationMaintained by Karayolları Genel MüdürlüğüLength30,974 km (2021) (19,246 mi)Formed1950Highway namesDevlet Yolu:D.XXXSystem links Highways in Turkey Motorways List State Highways List The State Highways of the Republic of Turkey (Turkish: Türkiye Cumhuriyeti Devlet Karayolları), abbreviated as T.C.K. are an integrated network of h...

Grade I listed building in York, England Yorkshire MuseumLocation within North YorkshireEstablished1830; 194 years ago (1830)LocationMuseum Gardens, York, EnglandCoordinates53°57′42″N 1°05′15″W / 53.9618°N 1.0875°W / 53.9618; -1.0875TypeArchaeological and Natural Sciences MuseumVisitors163,805 (2018–19)[1]DirectorReyahn King, York Museums TrustWebsiteyorkshiremuseum.org.uk The Yorkshire Museum is a museum in York, England. It was...

Sporting event delegationPuerto Rico at the1972 Summer OlympicsIOC codePURNOCPuerto Rico Olympic CommitteeWebsitewww.copur.pr (in Spanish)in MunichCompetitors53 in 10 sportsFlag bearer Arnaldo Bristol[1]Medals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)19481952195619601964196819721976198019841988199219962000200420082012201620202024 Puerto Rico competed at the 1972 Summer Olympics in Munich, West Germany. 53 competitors, all men, took part in 37 ev...

1955 Liberian general election ← 1951 3 May 1955 1959 → Presidential election Nominee William Tubman Edwin Barclay Party TWP ITWP Popular vote 244,873 1,182 Percentage 99.51% 0.48% President before election William Tubman TWP Elected President William Tubman TWP Politics of Liberia Constitution 1847 Constitution 1986 Constitution Executive President Joseph Boakai Vice President Jeremiah Koung Cabinet Legislature Senate President Pro Tempore House of Represent...

Elections to the Baseball Hall of Fame This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1967 Baseball Hall of Fame balloting – news · newspapers · books · scholar · JSTOR (October 2019) (Learn how and when to remove this message) 1967 Baseball Hall of Fame ballotingNew inductees3via BBWAA1via Veterans Committ...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: マキタスポーツ – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2012年12月) マキタスポーツ本名 槙田 雄司(まきた ゆ...

الإصلاح الإنجليزي هو مصطلح يعبر عن سلسلة من الأحداث التي مرت بها إنجلترا في القرن السادس عشر، والتي أدت لانفصال كنيسة إنجلترا عن سلطة البابا والكنيسة الكاثوليكية. ارتبطت هذه الأحداث بعملية أوروبية أوسع وهي عملية الإصلاح البروتستانتي، وهي حركة دينية وسياسية أثرت على ممار...

2021 Spanish filmDogtanian and the Three MuskehoundsEnglish theatrical release posterSpanishD'Artacán y los Tres Mosqueperros Directed byToni GarcíaScreenplay byDoug LangdaleBased onDogtanian and the Three MuskehoundsMusic byManel Gil-IngladaProductioncompanies Apolo Films Cosmos-Maya Distributed byA Contracorriente FilmsRelease dates 25 June 2021 (2021-06-25) (United Kingdom) 18 August 2021 (2021-08-18) (Spain) 2022 (2022) (North America) Run...