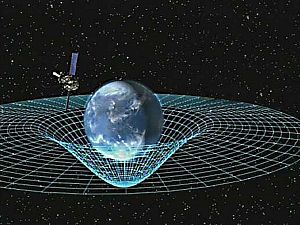
Ruang waktu
|
Read other articles:

Mir asad Ali Khan Chin Chilich Khan Nizam-Ul-Mulk Asaf Jah VIINizam Hyderabad MP GCSI GBEBerkuasaNizam: 1911–1948Pemegang gelar Nizam: 1948–1967Penobatan18 September 1911PendahuluMahbub Ali Khan, Asaf Jah VIPenerusMonarki dibubarkanKelahiran(1886-04-06)6 April 1886Purani Haveli, Hyderabad, Negara Hyderabad, India Britania(kini di Andhra Pradesh, India)Kematian24 Februari 1967 (usia 80)Istana King Kothi, Hyderabad, Andhra Pradesh, IndiaPemakamanMasjid Judi, Istana King Kothi, Hyderabad, An...

Salai PisangNama lainRimpi (Banjar), Dampo' Unti (Makassar), Dempo' Utti (Bugis), Sale Gedhang (Jawa)Tempat asalIndonesiaDaerahAcehSunting kotak info • L • BBantuan penggunaan templat iniSalai pisang basah Salai pisang atau Sale pisang adalah makanan hasil olahan pisang yang dibuat dengan proses pengeringan dan pengasapan, kemudian dipotong iris-iris dan dijemur. Salai pisang dikenal mempunyai rasa dan aroma khas yang cenderung lebih manis. Tujuan penjemuran adalah untuk mengura...

Prima Categoria 1907 Competizione Prima Categoria Sport Calcio Edizione 10ª Organizzatore Federazione Italiana Football Date dal 13 gennaio 1907al 27 aprile 1907 Luogo Italia Partecipanti 6 Formula Eliminatorie regionali + girone finale Risultati Vincitore Milan(3º titolo) Secondo Torino Terzo Andrea Doria Statistiche Miglior marcatore Hans Kämpfer (7) Incontri disputati 12 Gol segnati 36 (3 per incontro) Il Milan vincitore del suo terzo titolo nazionale Cronologia...

Jaksa Agung Amerika SerikatLambang Departemen Kehakiman Amerika SerikatPetahanaMerrick Garlandsejak 11 Maret 2021Dibentuk26 September 1789Pejabat pertamaEdmund Randolph Jaksa Agung Amerika Serikat adalah kepala Departemen Kehakiman Amerika Serikat yang berurusan dengan masalah-masalah hukum dan pejabat penegak hukum utama dalam pemerintah Amerika Serikat. Jaksa Agung dianggap sebagai pengacara utama pemerintah AS. Jaksa Agung diangkat oleh Presiden Amerika Serikat dan dikukuhkan oleh Sen...

2008 2015 Élections cantonales de 2011 dans le Tarn 23 des 46 cantons du Tarn 20 et 27 mars 2011 Type d’élection Élections cantonales Majorité départementale – Thierry Carcenac Liste PRGPSPCFDVG Sièges obtenus 31 Opposition départementale Liste UMPDVDMoDem Sièges obtenus 15 PRG : 13 sièges DVG : 2 siègesPS : 8 sièges DVD : 3 sièges DIV : 3 sièges UMP : 1 siège Président du Conseil général Sortant Élu Thierry Carcenac PS ...

Questa voce sull'argomento contee del Wisconsin è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di LincolnconteaLocalizzazioneStato Stati Uniti Stato federato Wisconsin AmministrazioneCapoluogoMerrill Data di istituzione1874 TerritorioCoordinatedel capoluogo45°10′50″N 89°41′00″W / 45.180556°N 89.683333°W45.180556; -89.683333 (Contea di Lincoln)Coordinate: 45°10′50″N 89°41′00″W / ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Anjing laut – berita · surat kabar · buku · cendekiawan · JSTORAnjing laut Pinnipedia TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoCarnivoraInfraordoPinnipedia Illiger, 1811 lbs Anjing laut (Be...

Missile attacks on Barda, Azerbaijan in October 2020 Barda missile attacksPart of the Second Nagorno-Karabakh WarLocationBarda, Əyricə, and Qarayusifli, AzerbaijanDate 27 October 2020 28 October 2020 7 November 2020 (GMT+4) Attack typeMissile attackWeapons Cluster missiles BM-30 Smerch Deaths27Injured85Perpetrators Armenian Armed Forces Artsakh Defence Army vteSecond Nagorno-Karabakh War Offensives and battles Madagiz Hadrut Aras Valley Lachin Shusha Bombings and shelling attacks Stepanake...

Mr. SocratesPoster teatrikalSutradaraChoi Jin-wonPemeranKang Shin-ilKim Rae-wonLee Jong-hyeokOh Kwang-rokYoon Tae-youngPenyuntingPark Gok-jiTanggal rilis 10 November 2005 (2005-11-10) NegaraKorea SelatanBahasaBahasa Korea Mr. Socrates (Hangul: 미스터 소크라테스) adalah film Korea Selatan tahun 2005 yang bertemakan cerita kriminal. Pranala luar Mr. Socrates di Korean Movie Database Mr. Socrates di IMDb (dalam bahasa Inggris) Artikel bertopik film Korea Selatan ini ad...

Classic rock radio station in New York City This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: WAXQ – news · newspapers · books · scholar · JSTOR (August 2021...

Art museum in Alicante, SpainAlicante Museum of Contemporary ArtMuseo de Arte Contemporáneo de AlicanteEstablished1977[1]LocationPlaza de Santa María, 3, Alicante, SpainCoordinates38°20′46.5″N 0°28′46.9″W / 38.346250°N 0.479694°W / 38.346250; -0.479694TypeArt museumCuratorPublic (city of Alicante)Websitewww.maca-alicante.es Alicante Museum of Contemporary Art (Spanish: Museo de Arte Contemporáneo de Alicante, MACA) is a municipal museum in Alican...

Cet article est une ébauche concernant une localité italienne et le Piémont. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chiusa di Pesio Armoiries Noms Nom français L'Écluse-de-Pez Nom occitan La Chuza Nom piémontais La Ciusa Administration Pays Italie Région Piémont Province Coni Code postal 12013 Code ISTAT 004068 Préfixe tel. 0171 Démographie Gentilé chiusani Population 3 783&#...

British politician (born 1967) The Right Honourable SirGraham BradyMPOfficial portrait, 2020Chairman of the 1922 CommitteeIncumbentAssumed office 20 January 2020Acting: 3 September 2019 – 20 January 2020LeaderBoris JohnsonLiz TrussRishi SunakPreceded byDame Cheryl Gillan andSir Charles WalkerIn office26 May 2010 – 24 May 2019LeaderDavid CameronTheresa MayPreceded bySir Michael SpicerSucceeded byDame Cheryl Gillan and Sir Charles Walker Shadow portfolios Shadow Minister for Eu...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Andorran Basketball FederationSportBasketballJurisdictionAndorraAbbreviationFABFounded1988 (1988)AffiliationFIBARegional affiliationFIBA EuropeAffiliation date2001HeadquartersAndorra la VellaPresidentManuel FernándezOfficial websitewww.fab.ad The Andorran Basketball Federation (Catalan: Federació Andorrana de Basquetbol) is the governing body of basketball in Andorra. It was founded in 1988. It organizes the internal league and runs the Andorra national basketball team and also the men...

Theory in actuarial science and applied probability Risk theory redirects here. For another use, see Tirpitz Plan. In actuarial science and applied probability, ruin theory (sometimes risk theory[1] or collective risk theory) uses mathematical models to describe an insurer's vulnerability to insolvency/ruin. In such models key quantities of interest are the probability of ruin, distribution of surplus immediately prior to ruin and deficit at time of ruin. Classical model A sample path...

Neighborhood of Brooklyn in New York City Neighborhood of Brooklyn in New York CityFlatlandsNeighborhood of BrooklynJans Martense Schenck house, Flatlands, built 1675, formerly at Avenue U and East 63rd StreetLocation in New York CityCoordinates: 40°37′16″N 73°56′06″W / 40.621°N 73.935°W / 40.621; -73.935Country United StatesState New YorkCity New York CityBorough BrooklynCommunity DistrictBrooklyn 18[1]Area • Total2.2800 ...

Radio station in Colfax, WashingtonKMAXColfax, WashingtonBroadcast areaPullman–Moscow; South Eastern WashingtonFrequency840 kHzBrandingThe Max 840 AMProgrammingFormatTalk radioAffiliationsCompass Media NetworksPremiere NetworksSalem Radio NetworkWestwood OneOwnershipOwnerInland Northwest Broadcasting, LLCSister stationsKCLX, KRAO-FMHistoryFirst air dateJanuary 1998 (26 years ago) (1998-01)Former call signsKRAO (CP; 1995–96)Technical information[1]Licensing autho...

Archosaurian reptiles that dominated the Mesozoic Era For other uses, see Dinosaur (disambiguation). Not to be confused with Dinosaurus. DinosaursTemporal range: Late Triassic–Present, 233.23 – 0 Mya (range includes birds) PreꞒ Ꞓ O S D C P T J K Pg N (possible Middle Triassic record) Herrerasaurus ischigualastensis(a carnivorous basal dinosaur)Triceratops horridus(a ceratopsian)Stegosaurus stenops(a stegosaur)Apatosaurus louisae(a sauropod)Edmontosaurus regalis(a hadrosaurid ornithopo...

President of Somalia from 1969 to 1991 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Siad Barre – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this message) Jaalle Major GeneralSiad BarreMaxamed Siyaad Barre محمد زياد بري 𐒑𐒖𐒄𐒖𐒑𐒗𐒆 ...