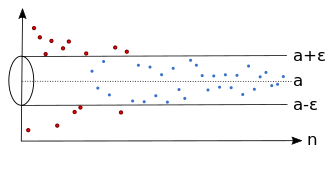
Limit barisan
| |||||||||||||||
Read other articles:

Artikel ini menggunakan gaya pengutipan yang tidak konsisten. Sumber referensi yang digunakan dapat diperbaiki dengan mengikuti pedoman pengutipan dan catatan kaki. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Dentsu Group Inc.Dentsu Building di Shiodome, TokyoNama asli株式会社電通JenisPublik (K.K)Kode emitenTYO: 4324IndustriPeriklananHubungan masyarakatInformasi, KomunikasiDidirikan1 Juli 1901; 122 tahun lalu (1901-07-01) (dengan nama Japan Advertising Ltd.)...

Biografi ini tidak memiliki sumber tepercaya sehingga isinya tidak dapat dipastikan. Bantu memperbaiki artikel ini dengan menambahkan sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus.Cari sumber: Jonathan Morgan Heit – berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Jonathan Morgan HeitLahirJonathan Morgan...

العلاقات الليبيرية الميانمارية ليبيريا ميانمار ليبيريا ميانمار تعديل مصدري - تعديل العلاقات الليبيرية الميانمارية هي العلاقات الثنائية التي تجمع بين ليبيريا وميانمار.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: و�...

Village in Corinthia, Greece Cenchreae redirects here. For the city of the ancient Troad, see Cenchreae (Troad). For the town of ancient Argolis, see Cenchreae (Argolis). Settlement in GreeceKechries ΚεχριέςSettlementKenchreai. Isis Temple, converted into basilica after the earthquake 365KechriesCoordinates: 37°53′6″N 22°59′15″E / 37.88500°N 22.98750°E / 37.88500; 22.98750CountryGreeceAdministrative regionPeloponneseRegional unitCorinthiaMunicipality...

ArrivaJenisAnak perusahaanKode emitenArrivaIndustriTransportasiDidirikan1938; 86 tahun lalu (1938)PendiriThomas CowieKantorpusatSunderland, InggrisWilayah operasiEropaTokohkunciManfred Rudhart (CEO)JasaLayanan bus, feri, dan kereta apiPendapatan€5,35 milyar (Desember 2017)Laba operasi€569 juta (Desember 2017)PemilikDeutsche BahnKaryawan61.845 (September 2018)DivisiArriva UK BusArriva UK TrainsMainland EuropeAnakusahaDaftar anak usahaSitus webwww.arriva.co.uk Arriva adalah s...
Kejuaraan Dunia BWF 2021 (2021 BWF World Championships)Informasi turnamenEdisike-26LevelInternasionalJadwalpenyelenggaraan12–19 DesemberTempatpenyelenggaraanPalacio de los Deportes Carolina Marín [es]Huelva, SpanyolNegara49 negaraPeserta322 pesertaLainnyaSitus web resmibwfworldchampionships.com ← Basel 2019 Tokyo 2022 → Kategori di Kejuaraan Dunia BWF 2021TunggalputraputriGandaputraputricampuranlbs Kejuaraan Dunia BWF 2021 (Inggris: 2021 BWF World Championships (nama resmi...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (mai 2014). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? Comme...

Welsh naturalist (1726–1798) Thomas PennantThomas Pennant by Thomas Gainsborough (1776)Born27 June [O.S. 14 June] 1726Downing Hall, Whitford, Flintshire, WalesDied16 December 1798(1798-12-16) (aged 72)Downing Hall, Whitford, Flintshire, WalesOccupationsNaturalistantiquarianKnown forWritings on natural history, geology, and geographical expeditions Thomas Pennant (27 June [O.S. 14 June] 1726 – 16 December 1798)[1] was a Wel...

Giuseppe Di Cristina Giuseppe Di Cristina (Riesi, 22 aprile 1923 – Palermo, 30 maggio 1978) è stato un mafioso italiano. Soprannominato la tigre nacque all'interno di una famiglia di consolidata tradizione mafiosa. Suo padre, Francesco Di Cristina, e suo nonno, Giuseppe soprannominato Birrittedda, erano a loro volta capi mafiosi. Nel 1961, alla morte di suo padre Francesco Di Cristina, prese in mano le redini della famiglia mafiosa di Riesi; Di Cristina era anche il rappresentante mafioso ...

City park in Atlanta, Georgia, United States of America This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chastain Park – news · newspapers · books · scholar · JSTOR (October 2018) (Learn how and when to remove this message) Chastain ParkLocationAtlanta, GeorgiaArea268 acres (1.08 km2)Created1940Operated&...

В Википедии есть статьи о других людях с такой фамилией, см. Василенко. Емельян Иванович Василенко Дата рождения 21 января 1901(1901-01-21) Место рождения ст. Роговская, Таманский отдел, Кубанская область, Российская империя[1] Дата смерти 28 июля 1976(1976-07-28) (75 лет) Место сме�...

Men's association football team This article is about the men's team. For the women's team, see England women's national football team. EnglandNickname(s)The Three LionsAssociationThe Football Association(The FA)ConfederationUEFA (Europe)Head coachGareth SouthgateCaptainHarry KaneMost capsPeter Shilton (125)Top scorerHarry Kane (63)Home stadiumWembley StadiumFIFA codeENG First colours Second colours FIFA rankingCurrent 4 1 (4 April 2024)[1]Highest3 (August–September 2012, September�...

Photographic process Daguerrotype redirects here. For the 2016 film, see Daguerrotype (film). Daguerreotype of Louis Daguerre in 1844 by Jean-Baptiste Sabatier-Blot Daguerreotype (/dəˈɡɛər(i.)əˌtaɪp, -(i.)oʊ-/ ⓘ;[1][2] French: daguerréotype) was the first publicly available photographic process, widely used during the 1840s and 1860s. Daguerreotype also refers to an image created through this process. Invented by Louis Daguerre and introduced worldwide in 1839,...

1998 Minnesota gubernatorial election ← 1994 November 3, 1998 2002 → Nominee Jesse Ventura Norm Coleman Skip Humphrey Party Reform Republican Democratic (DFL) Running mate Mae Schunk Gen Olson Roger Moe Popular vote 773,713 717,350 587,528 Percentage 37.0% 34.3% 28.1% County results Precinct resultsVentura: 30–40% 40–50% 50–60% 6...

В легендариуме Джона Р. Р. Толкина описывается значительное количество артефактов — предметов искусственного происхождения, сотворённых мастерами из числа Валар, детей Илуватара (эльфы и люди), гномов, а также Врагами (Моргот и Саурон). Ниже приведён список наибо...

Typographical symbol or glyph (*) * redirects here. For other uses, see Asterisk (disambiguation) and * (disambiguation). For the comic book series, see Asterix. *AsteriskIn UnicodeU+002A * ASTERISK (*, *)RelatedSee alsoU+203B ※ REFERENCE MARK (komejirushi) U+A673 ꙳ SLAVONIC ASTERISK Look up * or asterisk in Wiktionary, the free dictionary. The asterisk (/ˈæstərɪsk/ *), from Late Latin asteriscus, from Ancient Greek ἀστε�...

سيزار ميلشتاين (بالإنجليزية: César Milstein) معلومات شخصية الميلاد 8 أكتوبر 1927 [1][2][3] باهيا بلانكا[4] الوفاة 24 مارس 2002 (74 سنة) [1][2][3] كامبريدج مواطنة الأرجنتين المملكة المتحدة[5] عضو في الجمعية الملكية، والأكاديمية الوطن�...

この項目では、サッカー指導者について説明しています。ミハイロ1世については「ミハイロ・ペトロヴィチ」をご覧ください。 ミハイロ・ペトロヴィッチ サンフレッチェ広島監督時代(2010年)名前愛称 ミシャ[1]ラテン文字 Mihailo Petrovićキリル文字 Михаило Петровић基本情報国籍 オーストリア セルビア生年月日 (1957-10-18) 1957年10月18日(66歳)出身地 �...

Optical illusion This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Color phi phenomenon – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and ...

موريس توملينسون معلومات شخصية الميلاد 9 أبريل 1971 (53 سنة) الإقامة تورونتو مواطنة جامايكا الحياة العملية المدرسة الأم جامعة تورينوجامعة الهند الغربية المهنة محامٍ، وناشط حقوق المثليين [لغات أخرى][1] تعديل مصدري - تعديل موريس توملينسون (با...