PROFILPELAJAR.COM

Dalam teori grup, grup disiklik (notasi Dic_n or Q_4n,^[1] ⟨n,2,2⟩) adalah jenis tertentu dari grup non-abelian dari urutan 4n (n > 1). Ini adalah ekstensi dari grup siklik dari order 2 oleh grup siklik dari order 2n, memberikan nama di-sklilik . Dalam notasi urutan tepat grup, ekstensi ini dapat dinyatakan sebagai:

1\to C_{2n}\to {\mbox{Dic}}_{n}\to C_{2}\to 1.\,

Secara lebih umum, diberikan grup abelian hingga dengan elemen urutan-2, seseorang dapat mendefinisikan grup disiklik.

Definisi

Untuk setiap bilangan bulat n > 1, grup siklik Dic_n dapat didefinisikan sebagai subgrup dari unit kuaternion yang dihasilkan oleh

{\begin{aligned}a&=e^{i\pi /n}=\cos {\frac {\pi }{n}}+i\sin {\frac {\pi }{n}}\\x&=j\end{aligned}}

Secara lebih abstrak, seseorang dapat mendefinisikan grup siklik Dic_n sebagai grup dengan presentasi berikut^[2]

\operatorname {Dic} _{n}=\langle a,x\mid a^{2n}=1,\ x^{2}=a^{n},\ x^{-1}ax=a^{-1}\rangle .\,\!

Beberapa hal yang perlu diperhatikan yang mengikuti dari definisi ini:

x⁴ = 1
x²a^k = a^k+n = a^kx²
if j = ±1, then x^ja^k = a^−kx^j.
a^kx⁻¹ = a^k−naⁿx⁻¹ = a^k−nx²x⁻¹ = a^k−nx.

Jadi, setiap elemen Dic_n dapat ditulis secara unik sebagai a^kx^j, dimana 0 ≤ k < 2n dan j = 0 atau 1. Aturan perkalian diberikan oleh

$a^{k}a^{m}=a^{k+m}$
$a^{k}a^{m}x=a^{k+m}x$
$a^{k}xa^{m}=a^{k-m}x$
$a^{k}xa^{m}x=a^{k-m+n}$

Ini mengikuti itu Dic_n memiliki urutan 4n .^[2]

Ketika n = 2, grup disiklik adalah isomorfik ke grup kuaternion Q . Lebih umum lagi, ketika n adalah pangkat 2, grup disiklik isomorfik ke grup kuaternion umum.^[2]

Sifat

Untuk setiap n > 1, grup siklik Dic_n adalah grup non-abelian dengan urutan 4n . (Untuk kasus degenerasi n = 1, grup Dic₁ adalah grup siklik C₄, yang tidak dianggap siklik.)

Maka A = ⟨a⟩ menjadi subgrup Dic_n dihasilkan oleh a . Maka A adalah grup siklik berurutan 2n, jadi [Dic_n:A] = 2. Sebagai subgrup dari indeks 2 secara otomatis menjadi subgrup normal. Grup hasil bagi Dic_n/A adalah grup siklik berurutan 2.

Dic_n adalah dapat diselesaikan; perhatikan bahwa A adalah normal, dan menjadi abelian, dengan sendirinya dapat dipecahkan.

Grup dihedral biner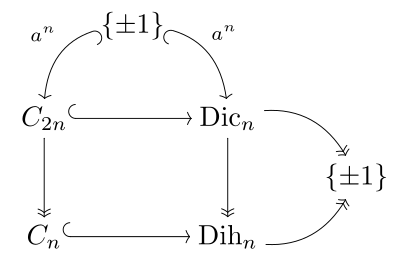

Grup disiklik adalah grup polihedral biner - ini adalah salah satu kelas subkelompok dari Grup pin Pin _-(2), yang merupakan subgrup dari Spin group Spin (3), dan dalam konteks ini dikenal sebagai grup dihedral biner.

Koneksi dengan grup siklik biner C_2n, grup siklik C_n, dan grup dihedral Dih_n dengan urutan 2n diilustrasikan dalam diagram di sebelah kanan, dan paralel dengan diagram yang sesuai untuk grup Pin. Coxeter menulis grup dihedral biner sebagai ⟨2,2,n⟩ dan grup siklik biner dengan tanda kurung siku, ⟨n⟩.

Ada kemiripan yang dangkal antara gugus disiklik dan gugus dihedral; keduanya adalah semacam "pencerminan" dari grup siklik yang mendasarinya. Tetapi presentasi dari grup dihedral akan memiliki x² = 1, instead of x² = aⁿ; dan ini menghasilkan struktur yang berbeda. Secara khusus, Dic_n bukan merupakan produk semidirect dari A dan ⟨x⟩, karena A ∩ ⟨ x ⟩ tidak trivial.

Gugus siklik memiliki involusi yang unik (yaitu elemen orde 2), yaitu x² = aⁿ. Perhatikan bahwa elemen ini terletak di pusat dari Dic_n. Memang, pusat hanya terdiri dari elemen identitas dan x². Jika kita menambahkan relasi x² = 1 untuk presentasi Dic_n one mendapatkan presentasi dari grup dihedral Dih_2n, jadi kelompok hasil bagi Dic_n/<x²> isomorfik untuk Dih_n.

Ada 2-ke-1 homomorfisme alami dari kelompok satuan quaternions ke 3-dimensi grup rotasi dijelaskan di kuaternion dan rotasi spasial. Karena grup disiklik dapat disematkan di dalam satuan quaternions, seseorang dapat bertanya apa gambarnya di bawah homomorfisme ini. Jawabannya hanyalah kelompok simetri dihedral Dih_n. Karena alasan ini, kelompok disiklik juga dikenal sebagai grup dihedral biner. Perhatikan bahwa grup disiklik tidak berisi subkelompok isomorfik apa pun Dih_n.

Konstruksi pra-gambar analog, menggunakan Pin₊(2) dari Pin₋(2), menghasilkan gugus dihedral lain, Dih_2n, bukan grup siklik.

Generalisasi

Misalkan A menjadi grup abelian, memiliki elemen tertentu y di A dengan urutan 2. Grup G disebut grup disiklik umum, ditulis sebagai Dic(A, y), jika itu dihasilkan oleh A dan elemen tambahan x , dan sebagai tambahan kami memilikinya [G:A] = 2, x² = y, dan untuk a in A, x⁻¹ax = a⁻¹.

Karena untuk grup siklik berorde genap, selalu ada elemen unik dari orde 2, kita dapat melihat bahwa grup siklik hanyalah tipe spesifik dari grup disiklik umum.

Lihat pula

grup polihedral biner
grup siklik biner, ⟨n⟩, urutan 2n
grup tetrahedral biner, 2T=⟨2,3,3⟩, urutan 24
grup oktahedral biner, 2O=⟨2,3,4⟩, urutan 48
grup ikosahedral biner, 2I=⟨2,3,5⟩, urutan 120

Referensi

^ Nicholson, W. Keith (1999). Introduction to Abstract Algebra (edisi ke-2nd). New York: John Wiley & Sons, Inc. hlm. 449. ISBN 0-471-33109-0.
^ ^a ^b ^c Roman, Steven (2011). Fundamentals of Group Theory: An Advanced Approach. Springer. hlm. 347–348. ISBN 9780817683016.

Coxeter, H. S. M. (1974), "7.1 The Cyclic and Dicyclic groups", Regular Complex Polytopes, Cambridge University Press, hlm. 74–75 .
Coxeter, H. S. M.; Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.