Grup topologi
|
Read other articles:

Boys BeAlbum mini karya SeventeenDirilis10 September 2015 (2015-09-10)GenreK-popdance-pophip hopDurasi15:51BahasaKoreaLabelPledis EntertainmentLOEN EntertainmentKronologi Seventeen 17 Carat(2015) Boys Be(2015) Love & Letter(2016) Singel dalam album Boys Be MansaeDirilis: 10 September 2015 Boys Be adalah album mini kedua dari boy band asal Korea Selatan Seventeen. Album ini dirilis pada tanggal 10 September 2015, oleh Pledis Entertainment. Album ini terdiri dari lima lagu, termasu...

Cet article concerne la langue japonaise. Pour le peuple japonais, voir Japonais (peuple). Japonais日本語 (nihongo) Pays Japon Nombre de locuteurs environ 128 millions (2020) Nom des locuteurs Japonophones[1], ou Nipponophones Typologie SOV, agglutinante, accusative, morique, à accent de hauteur Écriture Kanjis et kanas (hiraganas et katakanas) Classification par famille - langues japoniques - langues japoniques insulaires - vieux japonais - japonais Statut officiel Langue officiell...

Men's quadruple sculls at the 2017 World Rowing ChampionshipsVenueNathan Benderson ParkLocationSarasota, United StatesDates24–30 SeptemberCompetitors61 from 15 nationsWinning time5:43.10Medalists Dovydas NemeravičiusMartynas DžiaugysRolandas MaščinskasAurimas Adomavičius Lithuania Jack BeaumontJonathan WaltonJohn CollinsGraeme Thomas Great Britain Kaur KuslapAllar RajaTõnu EndreksonKaspar Taimsoo EstoniaU...

У этого термина существуют и другие значения, см. Дихотомия (значения). Дихотомия Инь и Ян Дихотоми́я (греч. διχοτομία: δῐχῆ, «надвое» + τομή, «деление») — раздвоенность, последовательное деление на две части, более связанные внутри, чем между собой. Способ логического д...

SMA Negeri 1 GarutSekolah Menengah Atas Negeri 1 GarutInformasiDidirikan1958JenisNegeriAkreditasiAKepala SekolahDrs. Sumpena Permana Putra, SH, M.MPd. (2020-Sekarang)Jumlah kelas36 kelas semua tingkatJurusan atau peminatanMIPA dan IPSRentang kelasX MIPA, X IPS, XI MIPA, XI IPS, XII MIPA, dan XII IPSKurikulumKurikulum MerdekaAlamatLokasiJalan Merdeka No. 91, Kabupaten Garut, Jawa Barat, IndonesiaTel./Faks.+62 262 233782Situs webwww.sman1garut.sch.idMotoMotoMelayani dengan hati y...

Dutch politician In this Dutch name, the surname is de Rouwe.Sander de RouweMember of the House of RepresentativesIn office1 March 2007 – 20 May 2015 Personal detailsBorn (1980-11-01) November 1, 1980 (age 43)Bolsward, NetherlandsPolitical partyChristian Democratic AppealOccupationPolitician Sander de Rouwe (born 1 November 1980 in Bolsward) is a Dutch politician. As a member of the Christian Democratic Appeal he was a member of the House of Representatives between 1 March 200...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Pasak pondasi HurriPasak pondasi Hurri di LouvreBahan bakutembaga, batu kapurUkuranLouvre: 122 cm × 85 cm (48 in × 33 in)Met: 117 cm × 79 cm (46 in × 31 in)Sistem penulisanHuruf paku dalam bahasa HurriDibuatc. 2300—ca. 2159 BCEPeriodeKekaisaran Akkadia/HurriDitemukanTidak diketahuiTempat ditemukanKuil Nergal, Urkesh, SuriahLokasi sekarangMusée du Louvre, ParisMetropolitan Museum of Art, New YorkIdentifikasiLouvre: ...
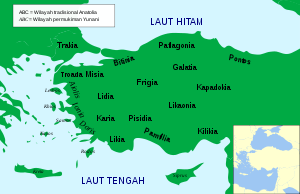
Peta Kapadokia di Anatolia. Kalender Kapadokia adalah penanggalan surya yang diturunkan dari kalender Zoroaster. Kalender ini dinamakan setelah daerah bersejarah Kapadokia di Anatolia (kini bagian dari Turki). Kalender ini memiliki 12 bulan yang masing-masing terdiri atas 30 hari dan lima hari interkalasi, pada tahun 550 hingga 330 SM, ketika Kapadokia di bawah kekuasaan Kekaisaran Akhemeniyah. Kalender Kapadokia sangat mirip dengan kalender Zoroaster, yang dapat dilihat dalam nama dan tata p...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

الشكل 1: تنسيق مخطط كتلة التدفق الوظيفي.[1] مخطط التدفق الوظيفي (اختصارًا FFBD) هو مخطط تدفق متعدد المستويات ومتسلسل زمنيًا خطوة بخطوة للتدفق الوظيفي للنظام.[2] يختلف مصطلح وظيفي في هذا السياق عن استخدامه في البرمجة الوظيفية أو في الرياضيات، حيث يكون الاقتران وظيفي مع ا...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bangaram-class patrol vessel – news · newspapers · books · scholar · JSTOR (July 2019) (Learn how and when to remove this message) INS Baratang (T68) during Milan 2018 Class overview NameBangaram class BuildersGarden Reach Shipbuilders and Engineers Operators&#...

Artikel ini bukan mengenai [[:Paleografi, ilmu tentang tulisan-tulisan kuno]]. Rekonstruksi Paleogeografik memperlihatkan area Cekungan Appalachia pada masa Devon Tengah.[1] Paleogeografi (juga dieja sebagai palaeogeografi) adalah ilmu yang mempelajari tentang sejarah geografi. Istilah ini pada umumnya mengacu pada ilmu tentang fisik lanskap, tetapi bisa juga mengacu pada ilmu tentang lingkungan manusia atau budaya. Saat fokus pada khususnya pada ilmu tentang bentang alam, digunakan j...

System to measure the color of water by observing the spectrum of radiation leaving the water. Water Remote Sensing is the observation of water bodies such as lakes, oceans, and rivers from a distance in order to describe their color, state of ecosystem health, and productivity. Water remote sensing studies the color of water through the observation of the spectrum of water leaving radiance. From the spectrum of color coming from the water, the concentration of optically active components of ...

Danish football club Football clubAaBFull nameAalborg Boldspilklub af 1885Nickname(s)De røde (The reds), De bolchestribede (The candy-cane striped)Short nameAaBFounded13 May 1885;139 years ago (1885-05-13)GroundAalborg Portland Park, AalborgCapacity13,800[1] (7,700 seated)OwnerAaB A/SSports directorOle Jan KappmeierHead coachMenno van DamLeagueSuperliga2023–241. Division, 2nd of 12 (promoted)WebsiteClub website Home colours Away colours Current season AaB,[2] ...

American geologist Newton Horace Winchell Newton Horace Winchell (17 December 1839 – 2 May 1914) was an American geologist chiefly notable for his six-volume work The Geology of Minnesota: Final Report of the Geological and Natural History Survey of Minnesota, which was prepared by Winchell and his assistants. A bibliography of his publications by Warren Upham in the Bulletin of the Geological Society of America (volume 26, pp. 27–46) contains almost 300 titles. Biography Born in...

Academic publisher based in the United Kingdom and the United States Adam Matthew DigitalParent companySAGE PublicationsFounded1990; 34 years ago (1990)FounderDavid TylerWilliam PidduckCountry of originUnited KingdomHeadquarters locationMarlborough, WiltshirePublication typesdatabasesOfficial websitewww.amdigital.co.uk Adam Matthew Digital is an academic publisher based in the United Kingdom and the United States. It has been an independent subsidiary of SAGE Publicatio...

Úrvalsdeild 2016Pepsi Úrvalsdeild 2016 Competizione Úrvalsdeild Sport Calcio Edizione 105ª Organizzatore KSI Date dal 1º maggio 2016al 1º ottobre 2016 Luogo Islanda Partecipanti 12 Formula girone all'italiana Risultati Vincitore FH Hafnarfjörður(8º titolo) Secondo Stjarnan Retrocessioni Fylkir Þróttur Statistiche Miglior marcatore Garðar Gunnlaugsson (14) Incontri disputati 132 Gol segnati 361 (2,73 per incontro) Cronologia della com...

داليمونت باركمعلومات عامةالمنطقة الإدارية Phibsborough (en) — دبلن البلد جمهورية أيرلندا التشييد والافتتاحالتجديد 1999الاستعمالالرياضة كرة القدم المستضيف نادي بوهيميان المالك نادي بوهيميان معلومات أخرىالطاقة الاستيعابية 7955الأرضية عشبيةالموقع الجغرافيالإحداثيات 53°21′42″N ...

日本の政治家石井 啓一いしい けいいち 2023年3月15日、首相官邸生年月日 (1958-03-20) 1958年3月20日(66歳)出生地 日本 東京都豊島区出身校 東京大学工学部土木工学科前職 建設省技官所属政党 (公明党→)(公明新党→)(新進党→)(新党平和→)公明党称号 工学士公式サイト 公明党幹事長 衆議院議員 石井啓一オフィシャルサイト 第20-21代 国土交通大臣内閣 第3次安�...




























































