Peta linear
|
Read other articles:

General election for Gujarat Indian general election in Gujarat, 2014 ← 2009 April–May 2014 2019 → 26 seatsTurnout63.66% (15.76%) First party Second party Party BJP INC Alliance NDA UPA Last election 15 seats 11 seats Seats won 26 0 Seat change 11 11 Gujarat In the 2014 Indian general election for Gujarat that were held for 26 seats in the state, the major two contenders in the state were Bharatiya Janta Party (BJP) and the Indian National ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

American college football season 2012 SMU Mustangs footballHawaii Bowl championHawaii Bowl, W 43–10 vs. Fresno StateConferenceConference USADivisionWest DivisionRecord7–6 (5–3 C-USA)Head coachJune Jones (5th season)Co-offensive coordinatorJason Phillips (1st season)Offensive schemeRun and shootDefensive coordinatorTom Mason (5th season)Base defense3–4Home stadiumGerald J. Ford StadiumSeasons← 20112013 → 2012 Conference USA football s...

Halaman ini berisi artikel tentang gunung di Papua Tengah. Untuk kabupaten, lihat Kabupaten Puncak Jaya. Untuk kabupaten, lihat Kabupaten Puncak. Puncak JayaNemangkawi Ninggok (Amungkal)Gunung Puncak JayaTitik tertinggiKetinggian4.884 m (16.024 ft)[1]Masuk dalam daftarTujuh PuncakKoordinat04°04′44″N 137°09′31″E / 4.07889°N 137.15861°E / 4.07889; 137.15861Koordinat: 04°04′44″N 137°09′31″E / 4.07889°N 137.15861°E&...

Gérard DepardieuGérard Depardieu di Festival Film Cannes tahun 2010LahirGérard Xavier Marcel Depardieu27 Desember 1948 (umur 75)Châteauroux, Indre, FranceWarga negara Prancis RusiaTahun aktif1964–sekarangSuami/istriÉlisabeth Guignot (m. 1971–1996)PasanganCarole Bouquet (1997–2005)Clémentine Igou (2005–sekarang)AnakGuillaume (meninggal), Julie, Roxanne, Jean Gérard Xavier Marcel Depardieu (lahir 27 D...

Ukrainian nationalist activist (1927-1968) You can help expand this article with text translated from the corresponding article in Ukrainian. (September 2021) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do n...

2020 Vermont Democratic primary 2020 Vermont Democratic presidential primary ← 2016 March 3, 2020 2024 → ← UTVA →24 delegates (16 pledged, 8 unpledged)to the Democratic National ConventionThe number of pledged delegates won is determined by the popular vote Candidate Bernie Sanders Joe Biden Home state Vermont Delaware Delegate count 11 5 Popular vote 79,921 34,669 Percentage 50.57% 21.94% Candidate Elizabeth Warren Mich...

Programmable calculator produced by Texas Instruments TI-55a TI-55TypeProgrammableManufacturerTexas InstrumentsIntroduced1977Discontinued1979CalculatorPrecision11 Floating point (within display)Display typeLEDDisplay size8+2CPUProcessorTI TMC1503NLOtherPower supplybattery / cellsPower consumption2 LR44'sWeight84 grams (3.0 oz)Dimensions147 mm × 71 mm × 22 mm (5.8 in × 2.8 in × 0.85 in) TI-55 II Calculator, the second variant, with an ...

Traditional Cantonese dish This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Soy sauce chicken – news · newspapers · books · scholar · JSTOR (September 2014) (Learn how and when to remove this template message) Soy sauce chickenCourseMain dishesPlace of originChinaRegion or stateGuangdongMain ingredientschicke...

Cetakan karbon karya W. & D. Downey, yang diterbitkan pada 1893 Sidney James Webb, 1st Baron Passfield, OM, PC (13 Juli 1859 – 13 Oktober 1947) adalah seorang sosialis, ekonom dan reformator Britania Raya, yang menjadi salah satu pendiri London School of Economics. Ia adalah anggota awal Fabian Society pada 1884, yang bergabung pada tiga bulan setelah pembentukannya, seperti George Bernard Shaw. Bersama dengan istrinya Beatrice Webb beserta dengan Annie Besant, Gra...

Standard RGB color space For the ancillary chunk in the PNG file format, see PNG § Ancillary chunks. sRGBIEC 61966-2-1 Default RGB Colour Space - sRGBsRGB colors situated at calculated position in CIE 1931 chromaticity diagram. Luminance Y {\displaystyle Y} set so that R + G + B = 1 {\displaystyle R+G+B=1} to avoid mach bands.AbbreviationsRGBStatusPublishedYear started1996First publishedOctober 18, 1999; 24 years ago (1999-10-18)[1]OrganizationIEC[1]Com...
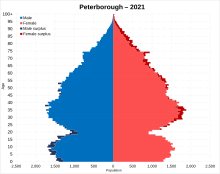
City and Unitary Authority in Cambridgeshire, England This article is about the local government district. For the individual settlement, see Peterborough. For other uses, see Peterborough (disambiguation). City and unitary authority in EnglandCity of PeterboroughCity and unitary authorityPeterborough viewed from the top of the cathedralCity of Peterborough shown within CambridgeshireCoordinates: 52°34′21″N 00°14′35″W / 52.57250°N 0.24306°W / 52.57250; -0.2...

Ebel CobraLahirAhmad Najmi HidayatPalangka Raya, Kalimantan Tengah, IndonesiaNama lainEbel CobraEbel CastanyoPekerjaanpelawak tunggalaktorTahun aktif2015—sekarangSuami/istriSilvy Diary (m. 2020) Ahmad Najmi Hidayat, yang lebih dikenal sebagai Ebel Cobra atau Ebel Castanyo merupakan seorang pelawak tunggal dan aktor berkebangsaan Indonesia.[1] Karier Ia tergabung dalam komunitas Stand Up Indo Jakarta Pusat dan berhasil menjadi juara ketiga da...

Progress 29A Progress 7K-TG spacecraftMission typeMir resupplyCOSPAR ID1987-034A SATCAT no.17878[1] Spacecraft propertiesSpacecraftProgress (No.127)Spacecraft typeProgress 7K-TG[2]ManufacturerNPO Energia Start of missionLaunch date21 April 1987, 15:14:17 UTC[1]RocketSoyuz-U2[2]Launch siteBaikonur, Site 1/5 End of missionDisposalDeorbitedDecay date11 May 1987, 07:51:16 UTC[3] Orbital parametersReference systemGeocentricRegimeLow EarthPerigee altitu...

1961 novel by John le Carré Call for the Dead First editionAuthorJohn le CarréLanguageEnglishSeriesGeorge SmileyGenreCrime, spy novelPublished1961PublisherGollanczPublication placeUnited KingdomMedia typePrint (hardback & paperback)Pages157 ppISBN0-7434-3167-7Followed byA Murder of Quality Call for the Dead is John le Carré's first novel, published in 1961. It introduces George Smiley, the most famous of le Carré's recurring characters, in a story about East German spi...

Unpleasant mental state Annoy redirects here. For the minesweeper, see USS Annoy (AM-84). For the website, see annoy.com. For the comedy club, see Annoyance Theatre. Part of a series onEmotions Affect Classification In animals Emotional intelligence Mood Self-regulation Interpersonal Dysregulation Valence Emotions Acceptance Admiration Affection Amusement Anger Angst Anguish Annoyance Anticipation Anxiety Apathy Arousal Awe Belongingness Boredom Confidence Confusion Contempt Contentment Coura...

Portugal i olympiska spelen IOK-landskodPOR KommittéPortugals Olympiska KommittéOlympiska sommarspelen 1948 i LondonDeltagare48 deltagare i 8 grenar Medaljsummering Guld0 Silver1 Brons1 Totalt2 Portugal i olympiska sommarspelen1912 • 1920 • 1924 • 1928 • 1932 • 1936 • 1948 • 1952 • 1956 • 1960 • 1964 • 1968 • 1972 • 1976 • 1980 • 1984 • 1988 • 1992 ...

German mathematician (1852–1939) Ferdinand von LindemannCarl Louis Ferdinand von LindemannBorn(1852-04-12)12 April 1852Hannover, German ConfederationDied6 March 1939(1939-03-06) (aged 86)Munich, GermanyNationalityGermanAlma materFriedrich-Alexander-Universität Erlangen-NürnbergKnown forProving π to be a transcendental numberLindemann–Weierstrass theoremScientific careerFieldsMathematicsInstitutionsUniversity of Munich, University of FreiburgDoctoral advisorC. Felix Klein...

Comics character Kanjar RoKanjar Ro as depicted in his debut appearance in Justice League of America #3 (February 1961); art by Murphy Anderson.Publication informationPublisherDC ComicsFirst appearanceJustice League of America #3 (February 1961)Created byGardner FoxMike SekowskyIn-story informationAlter egoKanjar RoPlace of originDhorTeam affiliationsR.E.B.E.L.S.AbilitiesBasic martial art skills, and possessed high tech weaponry, including a Gamma Gong that renders people motionless. This art...

Belgian racing driver Amaury CordeelCordeel driving the Dallara F2 2024 during the 2024 Spielberg Formula 2 round.Nationality BelgianBorn (2002-07-09) 9 July 2002 (age 22)Temse, BelgiumRelated toGhislain Cordeel (brother)FIA Formula 2 Championship careerDebut season2022Current teamHitech Pulse-EightCar number16Former teamsVan Amersfoort Racing, Invicta Virtuosi RacingStarts56 (56 entries)Wins0Podiums0Poles0Fastest laps1Best finish17th in 2022Previous series202120202019–20202019–20202...


























![{\displaystyle \int _{a}^{b}{[{{c}_{1}}{{f}_{1}}(x)+{{c}_{2}}{{f}_{2}}(x)+\ldots +{{c}_{n}}{{f}_{n}}(x)]dx}={{c}_{1}}\int _{a}^{b}{{{f}_{1}}(x)dx}+{{c}_{2}}\int _{a}^{b}{{{f}_{2}}(x)dx}+\ldots +{{c}_{n}}\int _{a}^{b}{{{f}_{n}}(x)dx}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d846ba13d174621b87518bfb239d5bc78fc91a0)
































