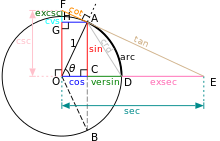
Lượng giác
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. TureiaTureiaTureiaGeografiLokasiSamudera PasifikKoordinat20°46′16″S 138°33′53″W / 20.77111°S 138.56472°W / -20.77111; -138.56472KepulauanTuamotuLuas47 km2 (laguna)8 km2 (3 sq mi) (dpl)Panj...

1985 studio album by The MekonsFear and WhiskeyStudio album by The MekonsReleased1985Recorded1984–1985GenreAlternative rock, alternative countryLength35:13LabelSinProducerMekonsThe Mekons chronology The Mekons Story(1983) Fear and Whiskey(1985) The Edge of the World(1986) Professional ratingsReview scoresSourceRatingAllMusic[1]Blender[2]Christgau's Record GuideA+[3]The Guardian[4]Pitchfork9.7/10[5]The Rolling Stone Album Guide[6]Spin ...

Presiden Republik IndonesiaLambang Negara IndonesiaLambang PresidenPetahanaJoko Widodosejak 20 Oktober 2014Pemerintah IndonesiaGelar Bapak Presiden (informal) Yang Terhormat (formal) Paduka Yang Mulia (tidak digunakan lagi) Kediaman Istana Negara Istana Merdeka Istana Bogor Istana Cipanas Gedung Agung Istana Tampaksiring Ditunjuk olehPemilihan umum langsungMasa jabatan5 tahun, dapat diperpanjang sekaliPejabat perdanaSoekarnoDibentuk18 Agustus 1945; 78 tahun lalu (1945-08-18)WakilWak...

Macerata miasto i gmina Panorama starego miasta od strony zachodniej Herb Państwo Włochy Region Marche Prowincja Macerata Kod ISTAT 043023 Burmistrz Sandro Parcaroli Powierzchnia 92,73 km² Wysokość 315 m n.p.m. Populacja (2015)• liczba ludności 42 750 • gęstość 464 os./km² Numer kierunkowy 0733 Kod pocztowy 62100 Położenie na mapie MarcheMacerata Położenie na mapie WłochMacerata 43°18′01″N 13°27′12″E/43,300278 13,453333 M...

Aleister CrowleyCrowley, 1902LahirEdward Alexander Crowley(1875-10-12)12 Oktober 1875Royal Leamington Spa, Warwickshire, EnglandMeninggal1 Desember 1947(1947-12-01) (umur 72)Hastings, East Sussex, England Aleister Crowley (lahir Edward Alexander Crowley 12 Oktober 1875 – 1 Desember 1947) adalah seorang penulis, hedonis, revolusionis seksual dari Inggris, dan seorang okultis.[1] Di sepanjang perjalanan hidupnya ia banyak memberikan pengaruh bagi perkembangan okult...

2012 2022 Élections législatives de 2017 dans les Landes 3 sièges de députés à l'Assemblée nationale 11 et 18 juin 2017 Type d’élection Élections législatives Campagne 22 mai au 10 juin12 juin au 16 juin Corps électoral et résultats Population 407 444 Inscrits 310 207 Votants au 1er tour 171 461 55,27 % 6,5 Votes exprimés au 1er tour 166 538 Votes blancs au 1er tour 3 460 Votes nuls au 1er tour 1 463 Votants au 2d tour 150...

Pour les articles homonymes, voir Franchet d'Espèrey. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (décembre 2023). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de...

American baseball player (born 1983) Baseball player Scott FeldmanFeldman with the Houston Astros in 2014PitcherBorn: (1983-02-07) February 7, 1983 (age 41)Kailua, Hawaii, U.S.Batted: LeftThrew: RightMLB debutAugust 31, 2005, for the Texas RangersLast MLB appearanceAugust 17, 2017, for the Cincinnati RedsMLB statisticsWin–loss record78–84Earned run average4.43Strikeouts882 Teams Texas Rangers (2005–2012) Chicago Cubs (2013) Baltimore Orioles (2013) Hou...

English astronomer (1912–2000) This article is about the astronomer. For the association footballer, see George Alcock (footballer). George AlcockMBEBornGeorge Eric Deacon Alcock(1912-08-28)28 August 1912Peterborough, Northamptonshire, EnglandDied15 December 2000(2000-12-15) (aged 88)Known forDiscovery of comets and novae George Eric Deacon Alcock, MBE (28 August 1912, in Peterborough, Northamptonshire[1] – 15 December 2000) was an English astronomer. He was one of the m...

Nordamerikansk central tidszon UTC−6 Central standard Time eller CST är den tidszonen som används i centrala USA[1] och Kanada och i största delen av Mexiko. Dess normaltid definieras som sex timmar efter UTC (koordinerad universell tid). På sommaren används sommartid i dessa länder (med små undantagna områden), vilket innebär fem timmar efter UTC på sommaren. Sommartiden kallas i USA för CDT (förkortning för Central Daylight Saving Time). Det är 7 timmars tidsskil...

Term for pirates engaged in illegal logging An 1853 map of the U.S. state of Michigan, where timber pirates devastated United States Navy lumber reserves along the Michigan coast. In the United States, a timber pirate is a pirate engaged in the illegal logging industry. History The term probably originated during the Timber Rebellion in 1853, when criminals mainly from the western Great Lakes region preyed on Michigan's government-owned supplies of lumber. When the government responded by con...

Season of television series Season of television series MasterChef JuniorSeason 8Promotional poster for season 8, featuring (2nd row, L to R) judges Aarón Sanchez, Gordon Ramsay, and Daphne OzJudges Gordon Ramsay Aarón Sanchez Daphne Oz No. of contestants16WinnerLiya ChuRunner-upGrayson Price No. of episodes16ReleaseOriginal networkFoxOriginal releaseMarch 17 (2022-03-17) –June 23, 2022 (2022-06-23)Season chronology← PreviousSeason 7Next →Season 9 The eighth s...

Pour les articles homonymes, voir Bacchus (homonymie). BacchusArtiste Michel-AngeDate 1497Type NuTechnique Statue en marbreDimensions (H × L) 203 × ? cmMouvement Renaissance italienneLocalisation Bargello modifier - modifier le code - modifier Wikidata Bacchus est une sculpture du grand peintre et sculpteur italien de la Renaissance Michel-Ange, conservée aujourd'hui au musée national du Bargello à Florence. Description Le Bacchus (1497) est une sculpture en marb...

La Grotte de Platon, attribué à Michiel Coxcie, milieu du XVIe siècle. Huile sur bois de peuplier. Musée de la Chartreuse, Douai. L’allégorie de la caverne est une allégorie exposée par Platon dans La République. Elle expose en termes imagés les conditions d'accession de l'humain à la connaissance du Bien, au sens métaphysique du terme, ainsi que la transmission de cette connaissance. L'allégorie met en scène des humains enchaînés et immobilisés dans une caverne. Ils to...

SMA Negeri 1 BontangLogo SMA Negeri 1 BontangInformasiDidirikan10 November 1984JenisNegeriKepala SekolahTiti Wurdiyanti, M. PdAlamatLokasiJl. D. I. Panjaitan Gg. Piano 11 No.59, Bontang, Kalimantan Timur, IndonesiaKoordinat0°08′05″N 117°29′53″E / 0.13469°N 117.49798°E / 0.13469; 117.49798Situs webwww.sman1-btg.sch.idMoto Sekolah Menengah Atas Negeri 1 Bontang merupakan Sekolah Menengah Atas Negeri yang berlokasi di Jl. D. I. Panjaitan Gg. Piano 11...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. SMP Negeri 3 BanjarmasinInformasiNomor Pokok Sekolah Nasional30304199Kepala SekolahH. Jumberi S.PdJumlah kelas21 KelasRentang kelasVII, VIII, IXKurikulumKurikulum 2013Jumlah siswa±730 SiswaAlamatLokasiJl. Pangeran Antasari No.107, Karang ...
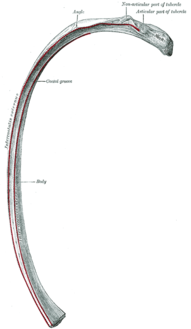
لمعانٍ أخرى، طالع ضلع (توضيح). ضلع (تشريح) الاسم العلميcosta أجزاء الضلع (وجه سفلي). تفاصيل نوع من عظم مسطح[1]، وعظم طويل[2]، وكيان تشريحي معين [لغات أخرى] ترمينولوجيا أناتوميكا 02.3.01.001 و A02.3.02.001 FMA 7574 UBERON ID 0002228 ن.ف.م.ط. A02.835.232.570.500 ن.ف.م.ط....

National broadcaster in Botswana Botswana TelevisionTypeBroadcastCountryBotswanaMottoTogether we are the future. (Mmogo re isago)Broadcast areaSouthern AfricaAreaGaborone, BotswanaOwnerGovernment of BotswanaLaunch date1965 (radio)2000 (television)Digital channel(s)(4:3) & (16:9)Picture format1080p (HDTV)Sister ChannelsBTV 1BTV 2BTV NewsNow ChannelRadio2 national radio stations and 3 privately ownedOfficial websitewww.btv.gov.bw Botswana Television (also known as BTV and Botswana TV) is th...

Giuseppe Peano Giuseppe Peano (Spinetta di Cuneo, 27 agosto 1858 – Cavoretto, 20 aprile 1932) è stato un matematico, logico e glottoteta italiano. Fra i maggiori matematici del periodo a cavallo fra XIX e XX secolo, fu anche l'ideatore del latino sine flexione, una lingua ausiliaria internazionale derivata dalla semplificazione del latino classico. Indice 1 Biografia 2 Attività scientifica 3 L'interlingua 4 Lo sforzo verso la semplificazione 5 Onorificenze 6 Opere 7 Dissero di lui 8 Note ...

У этого термина существуют и другие значения, см. Песуэла. Хоакин де ла ПесуэлаJoaquín de la Pezuela 53-й Вице-король Перу 7 июля 1816 — 29 января 1821 Монарх Фердинанд VII Предшественник Хосе Фернандо де Абаскаль Преемник Хосе де ла Серна Рождение 1761(1761)Наваль Смерть 1830(1830)Мадрид Профес...