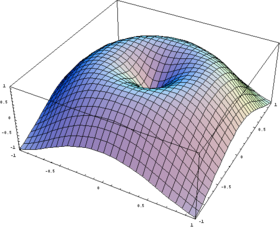
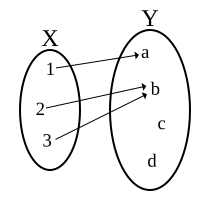
Функція (математика)
| |||||||||||||||||||||||||||
Read other articles:

Kawasaki KH-4 adalah sebuah helikopter utilitas cahaya yang diproduksi oleh Kawasaki di Jepang pada tahun 1960. Desain Kawasaki KH-4 merupakan pengembangan dari helikopter Bell 47. Jumlah unit Kawasaki KH-4 sebanyak 211 unit. Pembelian unit Kawasaki KH-4 terbagi antara operator sipil di Jepang, Angkatan Bersenjata Kekaisaran Jepang dan Angkatan Bersenjata Kerajaan Thailand. Desain Kawasaki KH-4 di desain melalui pengembangan desain helikopter Bell 47. Pengembangan utamanya pada pembuatan sis...

Jean-Louis Baudelocque Jean-Louis Baudelocque (30 November 1745 – 2 Mei 1810) merupakan seorang dokter kandungan dan profesor kebidanan Prancis. Dia adalah bidan paling terkenal pada masanya. Penulis L’art des accouchements, ia menjadikan ilmu kebidanan sebagai disiplin ilmu. Ia lahir di Heilly, di wilayah Prancis Picardie. Dia menyempurnakan forsep panggul André Levret (1703–1780) dan membuat jangka panggul untuk digunakan dalam kebidanan. Tulisan terpilih Principes sur l'art des acco...

العلاقات الغابونية الموريتانية الغابون موريتانيا الغابون موريتانيا تعديل مصدري - تعديل العلاقات الغابونية الموريتانية هي العلاقات الثنائية التي تجمع بين الغابون وموريتانيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدو�...

Coca-Cola Zero SugarJenisDiet ColaAsalAmerika SerikatDiperkenalkan2005ProdusenThe Coca-Cola CompanyVarianCoca-Cola Cherry Zero Coca-Cola Vanilla ZeroSitus webhttps://us.coca-cola.com/products/coca-cola-zero-sugar [sunting di Wikidata]lbs Coca-Cola Zero Sugar atau Coke Zero merupakan sebuah produk minuman yang diproduksi oleh The Coca-Cola Company. Minuman ini diluncurkan pada tahun 2005. Minuman ini umumnya menghasilkan 0% gula. Coca-Cola Zero Sugar merupakan terobosan baru yang dipe...
This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Rzeszów Voivodeship – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Rzeszów Voivodeship Rzeszów Voivodeship (Polish: województwo rzeszowskie) can refer to one of two political entities in Poland: Rzeszów Voi...

Commerzbank TowerInformasi umumJenisPerkantoranLokasiKaiserplatz 1 Frankfurt Hesse, JermanKoordinat50°06′38″N 8°40′27″E / 50.11056°N 8.67417°E / 50.11056; 8.67417Koordinat: 50°06′38″N 8°40′27″E / 50.11056°N 8.67417°E / 50.11056; 8.67417Mulai dibangun1994Pembukaan1997BiayaDM600 jutaPemilikdijual ke Samsung Insurance Corporation seharga €620 juta, dijual dan disewa kembali hingga 2031 oleh Commerzbank[1]TinggiMena...

Form of theatrical performance Street theatre outside the Centre Pompidou in Paris A troupe of street theatre performers by the beach in Vancouver, British Columbia, Canada. Acrobatics over Salvador: La Marioneta Gigante by Spanish company Carros de foc Street theatre is a form of theatrical performance and presentation in outdoor public spaces without a specific paying audience. These spaces can be anywhere, including shopping centres, car parks, recreational reserves, college or university ...

ジェイミー・オリヴァー(ニューヨークのユニオンスクエアにて) ジェイミー・オリヴァー(Jamie Oliver、本名:James Trevor Oliver, MBE、1975年5月27日 - )は、イギリスのシェフ。イギリスでは「裸のシェフ(Naked Chef)」として知られている。 来歴 イギリス・エセックスのClaveringで、パブ・レストラン「The Cricketers」を経営する両親の下に生まれる。8歳の頃より両親の手伝い...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Congregations of plankton Thin layer redirects here. For other uses, see Thin film. Visible layers of a red tide, a planktonic algal bloom, off the shores of Southern California Part of a series onPlankton Trophic mode Phytoplankton Zooplankton Mixoplankton Mycoplankton Bacterioplankton Virioplankton By size Heterotrophic picoplankton Microalgae Microzooplankton Nanophytoplankton calcareous Photosynthetic picoplankton Picoeukaryote Picoplankton Marine microplankton By taxonomy Algae diatoms c...

Saint-Floxel L'église Saint-Floxel. Administration Pays France Région Normandie Département Manche Arrondissement Cherbourg Intercommunalité Communauté d'agglomération du Cotentin Maire Mandat Joël Guilbert 2020-2026 Code postal 50310 Code commune 50467 Démographie Gentilé Saint-Floxelais Populationmunicipale 492 hab. (2021 ) Densité 58 hab./km2 Géographie Coordonnées 49° 29′ 31″ nord, 1° 21′ 04″ ouest Altitude Min. 15 mMax. ...

Indonesian Army Intelligence CenterPusat Intelijen TNI Angkatan Darat(Pusintelad)Indonesian Army Intelligence Center LogoFounded9 January 1978Country IndonesiaBranchIndonesian ArmyRoleIntelligence gathering for the Indonesian ArmyPart of Indonesian National Armed Forces (TNI)Motto(s)Satya Tanggap WaskitaWebsitetniad.mil.id/website/pusat-intelijenMilitary unit The Indonesian Army Intelligence Center (Indonesian: Pusat Intelijen TNI Angkatan Darat abbreviated Pusintelad) is one of the...

Elezioni presidenziali in Mongolia del 2021Stato Mongolia Data9 giugno Candidati Ukhnaagiin Khürelsükh Dangaasürengiin Enkhbat Sodnomzunduin Erdene Partiti MAN Zöv Khün AN Voti 823.32672,02% 246.96821,60% 72.8326,37% Distribuzione del voto per provincia Presidente uscenteKhaltmaagiin Battulga (AN) 2017 2025 Le elezioni presidenziali in Mongolia del 2021 si sono tenute il 9 giugno. Risultati Candidati Partiti Voti % Ukhnaagiin Khürelsükh Partito del Popolo Mongolo 823 326 72,...

Burial ground in Surrey, England Not to be confused with Rookwood Cemetery. Brookwood CemeteryThe Grade II* listed monument to Lord Edward Clinton at Brookwood Cemetery[1][2]DetailsEstablished1852LocationBrookwood, Surrey within Woking ancient parish and post townCountryUnited KingdomCoordinates51°17′48″N 00°38′00″W / 51.29667°N 0.63333°W / 51.29667; -0.63333Owned byWoking Necropolis and Mausoleum Limited, subsidiary of Woking Borough Counci...

Pour les articles homonymes, voir Chan. Tanya ChanTanya Chan en 2017.FonctionsMembre du Conseil législatif de Hong Kong6th Legislative Council of Hong Kong (en)Île de Hong Kong (en)depuis le 1er octobre 2016Membre du Conseil législatif de Hong Kong4th Legislative Council of Hong Kong (en)Île de Hong Kong (en)17 mai 2010 - 30 septembre 2012Membre du Conseil législatif de Hong Kong4th Legislative Council of Hong Kong (en)Île de Hong Kong (en)1er octobre 2008 - 28 janvier 2010Central and ...

American record label This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kill Rock Stars – news · newspapers · books · scholar · JSTOR (November 2020) (Learn how and when to remove this message) Kill Rock StarsFounded1991 (1991)FounderSlim MoonTinuviel SampsonDistributor(s)Redeye DistributionGenreRock, ind...

Clade of flowering plants MagnoliidsTemporal range: Aptian - recent[1][2] PreꞒ Ꞓ O S D C P T J K Pg N Flower of Asimina triloba Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Magnoliids Type species Magnolia virginiana Orders Canellales Laurales Magnoliales Piperales Magnoliids, Magnoliidae or Magnolianae are a clade of flowering plants. With more than 10,000 species, including magnolias, nutmeg, bay laurel, cinnamon, avocado, bla...

Herculez Gomez Informações pessoais Nome completo Hercules Gomez Hurtado Data de nascimento 6 de abril de 1982 (42 anos) Local de nascimento Los Angeles, Estados Unidos Altura 1,78 m Informações profissionais Clube atual Aposentado Posição ex-centroavante Clubes de juventude 2001–2002 Cruz Azul Clubes profissionais1 Anos Clubes Jogos e gol(o)s 20022002–2006200320042007–20082008–200920102010–201120112012–20132013–2015201420152015–20162016–2017 San...

Questa voce o sezione sull'argomento siti archeologici d'Italia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. MorgantinaPanorama dell'agorà ellenistica. In primo piano il Macellum di epoca romana e l'abitato della collina est. Sullo sfondo la Cittadella, il sito della Morgantina arcaica e l'Etna.CiviltàSicula, Greca, Romana UtilizzoCittà Localizzazi...

Timna Brauer Timna Brauer en 2008Informations générales Naissance 1er mai 1961 (63 ans)Vienne, Autriche Activité principale Chanteuse Genre musical Chanson, jazz, musiques du monde Années actives Depuis 1985 Site officiel www.brauer-meiri.com modifier Pour les articles homonymes, voir Timna (homonymie) et Brauer. Timna Brauer (née le 1er mai 1961 à Vienne) est une chanteuse israélo-autrichienne. Biographie Timna est la fille du peintre autrichien Arik Brauer et d'une Israélienne...