Теорія пружності
|
Read other articles:

Mr. BigI Mr. Big nel 1992. Da sinistra: Billy Sheehan, Paul Gilbert, Eric Martin, Pat Torpey (in basso) Paese d'origine Stati Uniti GenereAlbum-oriented rock[1]Pop metal[2][3]Hard rock[2]Hair metal[2][3]Heavy metal[2] Periodo di attività musicale1988 – 20022009 – in attività EtichettaAtlantic RecordsFrontiers Records Album pubblicati26 Studio9 Live12 Raccolte5 Logo ufficiale Sito ufficiale Mod...

Ini adalah nama Korea; marganya adalah Kwon. Kwon Hyuk-sooLahir6 Mei 1986 (umur 37)Korea SelatanPekerjaanAktor Nama KoreaHangul권혁수 Alih AksaraGwon Hyeok-suMcCune–ReischauerKwŏn Hyŏk-su Kwon Hyuk-soo (lahir 6 Mei 1986) adalah aktor asal Korea Selatan. Ia berperan dalam serial televisi seperti Lucky Romance (2016). Ia dikenal sebagai pembawa acara dari acara televisi Saturday Night Live Korea.[1] Referensi ^ Kwon, Bo-ra (14 June 2016). ['남사친' 인터뷰②] �...

All About My WifeNama lainHangul내 아내의 모든 것 Alih Aksara yang DisempurnakanNae anae-ui modeun geotMcCune–ReischauerNae anae-ŭi modŭn gŏt SutradaraMin Kyu-dongProduserPark Joon-ho Min Jin-soo Lee Yoo-jinDitulis olehHeo Sung-hye Min Kyu-dongBerdasarkanUn novio para mi mujeroleh Pablo SolarzPemeranIm Soo-jung Lee Sun-kyun Ryu Seung-ryongPenata musikLee Jin-hee Kim Jun-seongSinematograferKim Dong-youngPenyuntingKim Sun-minTanggal rilis 17 Mei 2012 (2012-05-17) Du...
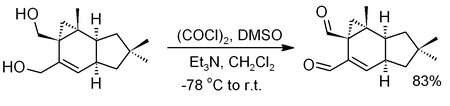
Organic redox reaction Swern oxidation Named after Daniel Swern Reaction type Organic redox reaction Identifiers Organic Chemistry Portal swern-oxidation RSC ontology ID RXNO:0000154 N(what is this?) (verify) In organic chemistry, the Swern oxidation, named after Daniel Swern, is a chemical reaction whereby a primary or secondary alcohol (−OH) is oxidized to an aldehyde (−CH=O) or ketone (>C=O) using oxalyl chloride, dimethyl sulfoxide (DMSO) and an organic base, such ...

Vice president of the United States from 1877 to 1881 For other people named William Wheeler, see William Wheeler (disambiguation). William A. WheelerWheeler in 187719th Vice President of the United StatesIn officeMarch 4, 1877 – March 4, 1881PresidentRutherford B. HayesPreceded byHenry WilsonSucceeded byChester A. ArthurMember of theU.S. House of Representativesfrom New YorkIn officeMarch 4, 1869 – March 3, 1877Preceded byCalvin T. HulburdSucceeded byAmaziah B. JamesCon...

Protected area in New South Wales, AustraliaBoonoo Boonoo National ParkNew South WalesIUCN category II (national park) Northern view of Boonoo Boonoo river from the falls lookout platformBoonoo Boonoo National ParkNearest town or cityTenterfieldCoordinates28°49′03″S 152°10′42″E / 28.81750°S 152.17833°E / -28.81750; 152.17833Established1982Area43.77 km2 (16.9 sq mi)[1]Managing authoritiesNational Parks and Wildlife Service (New South ...

Kazuha NakamuraLahir中村 一葉 (Kazuha Nakamura)09 Agustus 2003 (umur 20)Kochi, Jepang.KebangsaanJepangNama lain카즈하 KoreaTinggi170 cm (5 ft 7 in)Karier musikGenreK-popTahun aktif2022–sekarangLabelSource MusicArtis terkaitLe SserafimTanda tangan Kazuha Nakamura Nama Jepang Kanji: 中村 一葉 Hiragana: なかむら かずは Katakana: ナカムラ カズハ Alih aksara - Romaji: Nakamura Kazuha Nama Korea Hangul: 카즈하 Alih aksara - Romanisasi: Kajeuha...

Disambiguazione – Se stai cercando altri significati, vedi Paiva (disambigua). PaivacomuneLocalizzazioneStato Brasile Stato federato Minas Gerais MesoregioneZona da Mata MicroregioneJuiz de Fora AmministrazioneSindacoJair Toledo Paiva TerritorioCoordinate21°17′19″S 43°24′53″W / 21.288611°S 43.414722°W-21.288611; -43.414722 (Paiva)Coordinate: 21°17′19″S 43°24′53″W / 21.288611°S 43.414722°W-21.288611; -43.414722 (Paiva) A...

Portuguese online newspaper This article needs to be updated. Please help update this article to reflect recent events or newly available information. (November 2023) ObservadorFormatOnline NewspaperOwner(s)Observador On Time, S.A.Founder(s)António Carrapatoso, José Manuel Fernandes, Rui Ramos[1]PublisherJosé Manuel FernandesEditorMiguel PinheiroLanguagePortugueseHeadquartersLisbon, PortugalCirculation6,999,215 (Unique Visitors, November 2021)Websitewww.observador.pt Observador is ...

Photovoltaic power station near Primm, Nevada. Silver State North Solar ProjectCountryUnited StatesLocationClark CountyCoordinates35°37′36″N 115°21′12″W / 35.62667°N 115.35333°W / 35.62667; -115.35333StatusOperationalCommission dateMay 7, 2012Owner(s)First SolarSolar farm TypeFlat-panel PVfixed tiltSite area600 acresPower generationNameplate capacity60 MWp, 50 MWACCapacity factor27.0% (average 2013-2019)Annual ne...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Metolius, Oregon – news · newspapers · books · scholar · JSTOR (May 2010) (Learn how and when to remove this message) City in Oregon, United StatesMetolius, OregonCityCity of Metolius Welcome SignLocation in OregonCoordinates: 44°35′13″N 121°10′37″W&...

Government proceeding to remove an officeholder Photograph of the Senate during the 1999 impeachment trial of Bill Clinton In the United States, a federal impeachment trial is held as the second stage of the United States federal government's bifurcated (two-stage) impeachment process. The preceding stage is the impeachment itself, held by a vote in the United States House of Representatives.[1] Federal impeachment trials are held in the United States Senate, with the senators acting ...

Україна Ця стаття є частиною серії статей продержавний лад і устрійУкраїни Правова система Конституція Законодавство Права людини Глава держави Президент Володимир Зеленський Офіс Президента Керівник ОП Андрій Єрмак РНБОУ Секретар РНБОУ Олександр Литвиненко Державн...

Process of combining atomic nuclei This article is about the nuclear reaction. For its use in producing energy, see Fusion power. For the journal, see Nuclear Fusion (journal). For the song, see Nuclear Fusion (song). Not to be confused with Nuclear fission. The Sun is a main-sequence star, and thus releases its energy by nuclear fusion of hydrogen nuclei into helium. In its core, the Sun fuses 500 million tonnes of hydrogen each second. The nuclear binding energy curve. The formation of nucl...

Karta över rand- och bihav enligt Internationella sjöfartsorganisationen. Randhav är havsområden vid kontinenternas kuster som avgränsas från öppna havet av till exempel öar eller ökedjor. Randhav ligger oftast på kontinentalsockeln och är då grunda. Exempel på randhav är Nordsjön, Irländska sjön, Ochotska havet, Japanska havet, Lackadivsjön, Korallhavet och Berings hav.[1] Ett annat exempel är Gula havet öster om Kina. Se även Bihav Referenser ^ ”randhav - Uppslagsverk...

لمعانٍ أخرى، طالع اتصال (توضيح). اتصالاتمعلومات عامةصنف فرعي من تبادل معلومات يدرسه القائمة ... دراسات التواصلpragmatic information theory (en) علم التفاعلeducommunication (en) سوسيولوجيا التواصلسيكولوجية الاتصالات البيانات الخارجية متاحة في http://data.europa.eu/euodp/en/data/group/eurovoc_domain_100150 ممثلة بـ ...

American book publisher Basic BooksParent companyHachette Book GroupFounded1950FounderArthur Rosenthal[1]Country of originUnited StatesHeadquarters locationNew York CityOfficial websitewww.basicbooks.com Basic Books is a book publisher founded in 1950 and located in New York City, now an imprint of Hachette Book Group. It publishes books in the fields of psychology, philosophy, economics, science, politics, sociology, current affairs, and history. History Basic Books originated as a s...

French pastry This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Palmier – news · newspapers · books · scholar · JSTOR (November 2009) (Learn how and when to remove this message) PalmierA plate of palmiersAlternative namesPalm tree, elephant ear, pig's ear, prussiensTypePastryPlace of origin FranceMain ing...

For the umbrella term used to describe lung diseases cause by vaporizers, see Vaping-associated pulmonary injury. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vapi – news · newspapers · books · scholar · JSTOR (May 2012) (Learn how and when to remove this message) City in Gujarat, IndiaVapiCityJain Temple...

أربيل شعار نادي أربيل الاسم الكامل نادي أربيل الرياضي اللقب القلعة الصفراء الألوان الأسود والأصفر تأسس عام 1958 (باسم نادي بروسك) الملعب ملعب فرانسو حريريأربيل، العراق(السعة: 25,000) البلد العراق الدوري الدوري العراقي الدرجة الأولى 2022–23 المركز ا...




![{\displaystyle {\boldsymbol {\sigma _{ij}}}={\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}=\left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{matrix}}\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caac2e75b67674131271ba4a2c0a616961a72d40)

![{\displaystyle \varepsilon _{ij}={\frac {1}{2}}\left(u_{i,j}+u_{j,i}\right)=\left[{\begin{matrix}\varepsilon _{xx}&\varepsilon _{xy}&\varepsilon _{xz}\\\varepsilon _{yx}&\varepsilon _{yy}&\varepsilon _{yz}\\\varepsilon _{zx}&\varepsilon _{zy}&\varepsilon _{zz}\\\end{matrix}}\right]=\left[{\begin{matrix}{\frac {\partial u_{x}}{\partial x}}&{\frac {1}{2}}\left({\frac {\partial u_{x}}{\partial y}}+{\frac {\partial u_{y}}{\partial x}}\right)&{\frac {1}{2}}\left({\frac {\partial u_{x}}{\partial z}}+{\frac {\partial u_{z}}{\partial x}}\right)\\{\frac {1}{2}}\left({\frac {\partial u_{y}}{\partial x}}+{\frac {\partial u_{x}}{\partial y}}\right)&{\frac {\partial u_{y}}{\partial y}}&{\frac {1}{2}}\left({\frac {\partial u_{y}}{\partial z}}+{\frac {\partial u_{z}}{\partial y}}\right)\\{\frac {1}{2}}\left({\frac {\partial u_{z}}{\partial x}}+{\frac {\partial u_{x}}{\partial z}}\right)&{\frac {1}{2}}\left({\frac {\partial u_{z}}{\partial y}}+{\frac {\partial u_{y}}{\partial z}}\right)&{\frac {\partial u_{z}}{\partial z}}\\\end{matrix}}\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0b3df53b5a6ac48d7549e4ee45a0293fb9d7cb7)







