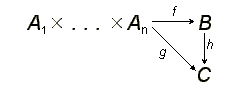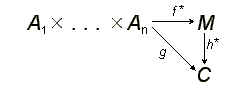Тензорний добуток
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Hans-Laurin BeyerlingLahirHans-Laurin BeyerlingPekerjaanaktor Hans-Laurin Beyerling (lahir 14 Oktober 1997) aktor dari Jerman. Dia mempunyai seorang kakak yang juga seorang aktris yaitu Lena Beyerling, dan dua orang adik lelaki, Hans Timo, yang juga s...

Not to be confused with Movimiento de Arte y Cultura Latino Americana. Commune in Auvergne-Rhône-Alpes, FranceMaclasCommune Coat of armsLocation of Maclas MaclasShow map of FranceMaclasShow map of Auvergne-Rhône-AlpesCoordinates: 45°21′47″N 4°41′07″E / 45.3631°N 4.6853°E / 45.3631; 4.6853CountryFranceRegionAuvergne-Rhône-AlpesDepartmentLoireArrondissementSaint-ÉtienneCantonLe PilatIntercommunalityPilat rhodanienGovernment • Mayor (2020̵...

Kompleks MusallahSisa Kompleks Musallah pada tahun 2005.HeratLokasi di AfganistanNama alternatifKompleks Musallah, Gauhar Shad MusallahLokasiHerat, AfganistanWilayahProvinsi HeratKoordinatKoordinat: 34°21′33″N 62°11′10″E / 34.359284°N 62.18608°E / 34.359284; 62.18608JenisKompleks keagamaan IslamTinggi55 m menara masjidSejarahPendiriRatu Goharshad dari Kekaisaran TimuriyahDidirikan1417Ditinggalkan1885BudayaIslamPeristiwa1885, dihancurkan BritaniaCatatan...

Dolok MerawanKecamatanKantor Kecamatan Dolok MerawanNegara IndonesiaProvinsiSumatera UtaraKabupatenSerdang BedagaiPemerintahan • Camat-Populasi • Total- jiwaKode Kemendagri12.18.07 Kode BPS1218040 Luas- km²Desa/kelurahan17/- Tanda selamat datang di Kecamatan Dolok Merawan Dolok Merawan adalah sebuah kecamatan di Kabupaten Serdang Bedagai, Sumatera Utara, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian ...

Dorce Sok AkrabSutradaraYazman YazidProduserRaam PunjabiDitulis olehDeddy ArmandPemeranDorce GamalamaKadirEko DJDoyokNurul ArifinJohny KaneHIM DamsyikSukarsihPak TileAcha HasanuddinDoddy SukmaRuslan EffendyWaylan GerungIta Puspita SariErna KurniawatiPenata musikBuche ChekingSinematograferSubakti ISPenyuntingBenny MSDistributorParkit FilmTanggal rilis1989Durasi84 menitNegaraIndonesia Dorce Sok Akrab adalah sebuah film Indonesia dirilis tahun 1989 yang disutradarai oleh Yazman Yazid serta...

American basketball coach (1915–2008) Ben CarnevaleCarnevale (left) with his assistant coach Pete Mullis during the 1944–45 seasonBiographical detailsBorn(1915-10-30)October 30, 1915Raritan, New Jersey, U.S.DiedMarch 25, 2008(2008-03-25) (aged 92)Williamsburg, Virginia, U.S.Playing career1933–1937NYU Coaching career (HC unless noted)1944–1946North Carolina1946–1966Navy Administrative career (AD unless noted)1966–1972NYU1972–1981William & Mary Head coaching recordOverall...

Peta Zuid en Ooster Afdeeling van Borneo, Lansdchap Cengal dan Manunggul berbatasan di utara dengan Kesultanan Paser dan di selatan dengan Landschap Sampanahan Kepangeranan Tjingal (Cengal) (d/h Kerajaan Pamukan), setelah bergabung dengan Hindia Belanda disebut Landschap Tjingal (Cengal) adalah sebuah Landschap atau suatu wilayah pemerintahan swaparaja yang dikepalai seorang bumiputera bagian dari Afdeeling Pasir en de Tanah Boemboe dalam pemerintahan kolonial Hindia Belanda di bawah kekuasaa...
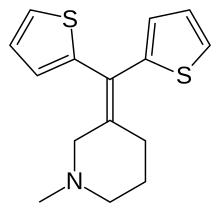
Chemical compound TipepidineClinical dataAHFS/Drugs.comInternational Drug NamesRoutes ofadministrationOralATC codeR05DB24 (WHO) Legal statusLegal status AU: S4 (Prescription only) Identifiers IUPAC name 3-(di-2-thienylmethylene)-1-methylpiperidine CAS Number5169-78-8 YPubChem CID5484ChemSpider5284 YUNII2260ZP67ITKEGGD08604 YCompTox Dashboard (EPA)DTXSID2022626 Chemical and physical dataFormulaC15H17NS2Molar mass275.43 g·mol−13D model (JSmol)Interactive im...

Photography and film term referring to framing a shot For other uses, see Close up (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Close-up – news · newspapers · books · scholar · JSTOR (May 2016) (Learn how and when to remove this message) Mexican actress Dolores del Río in a closeup publ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 9th Infantry Regiment United States – news · newspapers · books · scholar · JSTOR (September 2007) (Learn how and when to remove this message) 9th Infantry RegimentCoat of armsActive1855–PresentCountry United StatesBranch United States ArmyType...

Cet article concerne un positionnement politique. Pour le groupe parlementaire français du même nom, voir Extrême gauche (groupe parlementaire). Affiche du NPA en faveur de la Révolution tunisienne, à Besançon (Doubs, France). Le terme extrême gauche est employé depuis 1920 pour désigner une partie des groupes, mouvements, organisations et partis politiques, « qui se situent à la gauche du Parti communiste et du Parti socialiste »[1], dont les principaux furent d'ob...

историческое государство ИмперияЯпонская империяяп. 大日本帝國 Флаг Императорская печать Гимн: «Кими га ё» Японская империя в 1942 году Япония (1870—1905) Колонии Оккупированные территории (1932—1945) ↓ ↓ 3 января 1868 (29 ноября 1890) — 2 сентяб...

Rachid Ghezzal Nazionalità Francia Algeria (dal 2015) Altezza 182 cm Peso 65 kg Calcio Ruolo Centrocampista, Ala Squadra Beşiktaş CarrieraGiovanili 2004-2012 Olympique LioneSquadre di club1 2010-2017 Olympique Lione 254 (11)2012-2017 Olympique Lione87 (11)2017-2018 Monaco26 (2)2018-2019 Leicester City19 (1)2019-2020→ Fiorentina19 (1)2020- Beşiktaş101 (15)Nazionale 2013-2014 Francia U-204 (1)2015- Algeria22 (2) 1 I due numeri indican...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

الإبحار في الألعاب الأولمبية الصيفيةالهيئة الإداريةالاتحاد الدولي للإبحار [لغات أخرى]المنافسات10 (رجال: 5; سيدات: 4; مختلطة: 1)الألعاب 1896 1900 1904 1908 1912 1920 1924 1928 1932 1936 1948 1952 1956 1960 1964 1968 1972 1976 1980 1984 1988 1992 1996 2000 2004 2008 2012 2016 2020 قائمة الفائزين بالميداليات الإبحار إحدى الرياضات ا...
Kipchak Turkic language of Central Asia Not to be confused with Fuyu Kyrgyz language. KyrgyzКыргыз тилиقىرعىز تىلىKyrgyz written in Cyrillic and Perso-Arabic scriptsPronunciation[qɯɾʁɯzˈtʃɑ]Native toKyrgyzstan, Afghanistan, Tajikistan, Pakistan, ChinaRegionCentral AsiaEthnicityKyrgyzNative speakers5.15 million (2009 census)[1]Language familyTurkic Common TurkicKipchakKyrgyz–KipchakKyrgyzDialects Pamiri Kyrgyz Writing systemKyrgyz a...

Political party in Pakistan Baloch National Movement ChairmanNaseem Baloch[1]FounderGhulam Mohammed BalochFounded2004; 20 years ago (2004)Preceded byBalochistan National MovementIdeologyBaloch nationalismNational affiliationLeft Democratic FrontWebsitewww.thebnm.orgPolitics of PakistanPolitical partiesElections The Baloch National Movement is a Baloch nationalist[2] political organization which was led by Ghulam Mohammed Baloch, who served as the org...

Danie Theron Theron met fiets, 1899 Geboren 9 mei 1872Tulbagh, Britse Kaapkolonie Overleden 5 september 1900Gatsrand nabij Fochville, Zuid-Afrikaansche Republiek Land/zijde Zuid-Afrikaansche Republiek Dienstjaren 1899-1900 Rang Kapitein Eenheid Verkenners Bevel Theron se Verkenningskorps Slagen/oorlogen Tweede Boerenoorlog Daniël Johannes Stephanus Danie Theron (Tulbagh, 9 mei 1872 - Gatsrand, 5 september 1900) was de kapitein van de fietsinfanterie van de Boeren tijdens de Tweede Boerenoor...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) ديريك شيلبي معلومات شخصية الميلاد 4 مارس 1989 (35 سنة) هيوستن مواطنة الولايات المتحدة الطول 74 بوصة الوزن 280 رطل الحياة العملية المدرسة الأم ج�...

加拿大 加拿大政府与政治系列条目 王室 君主(歷任名單):查爾斯三世 總督(歷任名單):瑪麗·梅·西蒙 各省君主制(英语:Monarchy in the Canadian provinces) 省督 皇家特權 行政部門(國王會同樞密院) 樞密院 總理(歷任名單):賈斯汀·杜魯多 內閣(閣員名單(英语:List of Canadian ministries)):第29屆內閣 樞密院院長(英语:President of the King's Privy Council for Canada) 樞密�...