Алгоритм Крускала
|
Read other articles:

Gorkovsky avtomobilny zavod (GAZ)JenisPublik (RTS:GAZA)IndustriOtomotifDidirikan1929KantorpusatNizhny NovgorodProduk GAZ LDV LiAZSitus webSitus web resmi Gaz Group GAZ (RTS:GAZA) atau Gorkovsky avtomobilny zavod merupakan sebuah perusahaan multinasional yang bermarkas di Nizhny Novgorod. Didirikan pada tahun 1929 sebagai NNAZ, merupakan bagian dari Ford di Uni Soviet. Dari tahun 1935 hingga 1936 nama ini berganti menjadi imeni Molotova. Perusahaan ini menghasilkan berbagai macam produk kendar...

Brazilian footballer In this Portuguese name, the first or maternal family name is Azevedo and the second or paternal family name is Pedreira. Fernando Personal informationFull name Fernando Augusto Azevedo PedreiraDate of birth (1986-11-14) 14 November 1986 (age 37)Place of birth Salvador, BrazilHeight 1.79 m (5 ft 10 in)[1]Position(s) Left wingerLeft backTeam informationCurrent team KitcheeNumber 77Senior career*Years Team Apps (Gls)2010 Madre Deus 15 (1)2010...

العلاقات التشيكية الإستونية التشيك إستونيا التشيك إستونيا تعديل مصدري - تعديل العلاقات التشيكية الإستونية هي العلاقات الثنائية التي تجمع بين التشيك وإستونيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارن...

Street in Sydney, Australia Bathurst StreetNew South WalesBathurst StreetWest endEast endCoordinates 33°52′26″S 151°12′10″E / 33.873983°S 151.202814°E / -33.873983; 151.202814 (West end) 33°52′29″S 151°12′35″E / 33.874656°S 151.209734°E / -33.874656; 151.209734 (East end) General informationTypeStreetLength650 m (0.4 mi)[1]Major junctionsWest endHarbour StreetSydney CBD Sussex Street Kent S...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (أبريل 2022) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة �...
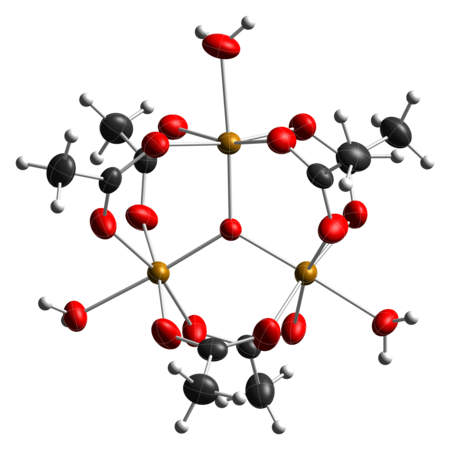
Iron(III) acetate[1] Names IUPAC name iron(III) acetate Other names basic iron(III) acetate , iron(III) oxyacetate, iron(III) Acetate Identifiers CAS Number 1834-30-6 Y 3D model (JSmol) Interactive imagecoordination complex: Interactive image ChemSpider 144555 PubChem CID 164887 UNII CZZ8832SI5 Y InChI InChI=1/3C2H4O2.Fe/c3*1-2(3)4;/h3*1H3,(H,3,4);/q;;;+3/p-3Key: PVFSDGKDKFSOTB-DFZHHIFOAZ SMILES CC(=O)[O-].CC(=O)[O-].CC(=O)[O-].[Fe+3]coordination complex: O1[...

Halaman ini berisi artikel tentang sejarah dan penerapan peraturan hukum yang pernah mengikat orang Tionghoa di Indonesia. Untuk pembahasan yang lebih luas tentang orang Tionghoa di Indonesia, lihat Tionghoa-Indonesia. Contoh surat permohonan penukaran nama Tionghoa, Januari 1968 Pada masa pemerintahan Soekarno (Orde Lama) dan Soeharto (Orde Baru), pemerintah Indonesia mengeluarkan beberapa peraturan perundang-undangan yang secara khusus mengatur masyarakat Tionghoa. Selepas Reformasi, sebagi...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...

Philippine television series Pera ParaanTitle card since 2023GenreInfotainmentPresented bySusan Enriquez[1]Country of originPhilippinesOriginal languageTagalogProductionCamera setupMultiple-camera setupProduction companyGMA Public AffairsOriginal releaseNetwork GMA News TV (2020–21) GTV (2021)[2] GMA Network (since 2021)[3] ReleaseJuly 22, 2020 (2020-07-22) –present Pera Paraan (transl. money way) is a Philippine television informative show broadcas...

Eitel-Frédéric Ier de Hohenzollern-Hechingen Titre Comte de Hohenzollern-Hechingen 28 mars 1576 – 16 janvier 1605(28 ans, 9 mois et 19 jours) Données clés Prédécesseur Création du titre Successeur Jean Georges de Hohenzollern-Hechingen Biographie Titulature Comte de Hohenzollern-Hechingen Dynastie Maison de Hohenzollern-Hechingen Nom de naissance Eitel Friedrich von Hohenzollern Naissance 7 septembre 1545Sigmaringen Décès 16 janvier 1605 (à 59 ans)Hechingen S�...

Cet article est une ébauche concernant la sculpture, l’Italie et le musée du Louvre. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. L'Esclave mourantArtiste Michel-AngeDate 1513-1516Type Statue en marbreDimensions (H × L × l) 228 × 72,4 × 53,5 cmMouvement Haute RenaissancePropriétaire État françaisNo d’inventaire MR 1590Localisation Musée du Louvre, Pari...

The Curse of the Cat PeoplePoster rilis teatrikal karya William RoseSutradara Robert Wise Gunther von Fritsch ProduserVal LewtonDitulis oleh DeWitt Bodeen Val Lewton (tak disebutkan) Pemeran Simone Simon Kent Smith Jane Randolph Ann Carter Eve March Penata musikRoy WebbSinematograferNicholas MusuracaPenyuntingJ.R. WhittredgeDistributorRKO Radio PicturesTanggal rilis 2 Maret 1944 (1944-03-02)[1] Durasi70 menitNegaraAmerika SerikatBahasaInggrisAnggaran$212.000 The Curse of th...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Bendera Chad Pemakaian Bendera nasional Perbandingan 2:3 Dipakai 6 November 1959 Rancangan Triwarna vertikal berwarna biru, emas dan merah. Bendera Chad terdiri dari tiga warna yaitu warna biru, kuning, dan merah. Bendera ini mirip bendera Rumania, bendera Andorra, dan bendera Moldova. Warna yang digunakan adalah warna gerakan Pan-Afrika dan bentuk tiga warna yang diubah dari bendera Italia. Bendera yang mirip Bendera Rumania Bendera Andorra Bendera Moldova Lihat pula Lambang Chad Bendera It...

سيلين، إلهة القمر في الأساطير الإغريقية (التمثال في الأصل يبين إلهة القمر الرومانية لونا، والتي تعد الإلهة المقابلة لسيليني) تعرف آلهة القمر في الميثولوجيا بأنها الآلهة المرتبطة برمز القمر.[1] وتملك هذه الآلهة وظائف وعادات مختلفة تبعاً للثقافة المتبنية لهذه الآلهة. غا...

FranceFIBA zoneFIBA EuropeNational federationFrench Federation of BasketballU21 World ChampionshipAppearances1Medals Silver: 1 (1993)U20 European ChampionshipAppearances23Medals Gold: 2 (2010, 2023) Silver: 2 (2009, 2012) Bronze: 4 (1992, 2002, 2011, 2017) The France men's national under-20 basketball team is a national basketball team of France, administered by the French Federation of Basketball.[1][2] It represents the country in men's international under-20 basketball com...

Joseph L. Bristow Ledamot av USA:s senat från Kansas Tid i befattningen4 mars 1909–3 mars 1915 Företrädare Chester I. Long Efterträdare Charles Curtis Född Joseph Little Bristow22 juli 1861Wolfe County, Kentucky Död 14 juli 1944 (82 år)Fairfax County, Virginia Gravplats Gypsum Hill CemeterySalina, Kansas Politiskt parti Republikanska partiet Alma mater Baker University Maka Margaret Hendrix (1879−1932; hennes död) Joseph Little Bristow, född 22 juli 1861 i Wol...

Mexican television series YagoAlso known asYago, pasión y venganzaGenreTelenovelaCreated byLarissa AndradeBased onThe Count of Monte Cristoby Alexandre DumasWritten by Fernanda Eguiarte Alejandra Olvera Tania Tinajero Julio Cérsar Mármol Story by Ay Yapım Karem Deren Pınar Bulut Directed by Rodrigo Curiel Eric Morales Alfredo Kassem Creative directorJorge GaskaStarring Iván Sánchez Gabriela de la Garza Flavio Medina Pablo Valentín Opening themeYagoComposerGiacomán de Neymet Alejandro...

Naval rank equivalent to lieutenant commander Corvette captain Common types of insigniaCountrySee galleryService branchNaviesRank groupSenior officerNATO rank codeOF-3Next higher rankFrigate captainNext lower rankShip-of-the-line lieutenantEquivalent ranksLieutenant commander (Anglophone) Naval officer ranks Flag officers Admiral of the fleet Grand admiral Admiral General admiral Vice admiral Squadron admiral Lieutenant admiral Rear admiral Admiral-superintendent Port admiral Counter admiral ...

Long bone of the upper arm Humeral redirects here. Not to be confused with humoral immunity. HumerusPosition of humerus (shown in red) from an anterior viewpointDetailsIdentifiersLatinhumerusMeSHD006811TA98A02.4.04.001TA21180FMA13303Anatomical terms of bone[edit on Wikidata] The humerus (/ˈhjuːmərəs/; pl.: humeri) is a long bone in the arm that runs from the shoulder to the elbow. It connects the scapula and the two bones of the lower arm, the radius and ulna, and consists of three se...







