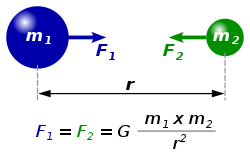
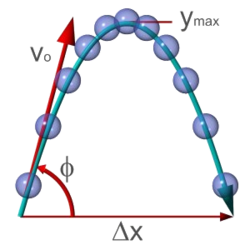
Класична механика
|
Read other articles:

Cummins Inc.SebelumnyaCummins Engine Company(1919–2001)JenisPublikKode emitenNYSE: CMIKomponen S&P 500Komponen DNS 100IndustriAlat berat, otomotifDidirikan1919; 105 tahun lalu (1919)PendiriClessie Lyle CumminsJ Irwin MillerKantorpusatCummins Corporate Office BuildingJalan Jackson nomor 500Columbus, Indiana, Amerika SerikatTokohkunciN. Thomas Linebarger(Chairman & CEO)Mark Smith(Wakil Presiden & CFO)ProdukMesin, filtrasi, pembangkit listrik, sistem sel bahan bakar, turbo...

Machimus divinosus Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Diptera Famili: Asilidae Genus: Machimus Spesies: Machimus divinosus Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Machimus divinosus – berita · surat kabar · buku&...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. NKoJangkauanU+07C0..U+07FF(64 titik kode)BidangBMPAksaraNKoAksara utamaMandenTerpakai59 titik kodeTak terpakai5 titik kode kosongRiwayat versi Unicode5.059 (+59) Catatan: [1] NKo adalah blok Unicode yang mengandung karakter untuk penulisan rumpun...

العلاقات الجزائرية النيبالية الجزائر نيبال الجزائر نيبال تعديل مصدري - تعديل العلاقات الجزائرية النيبالية هي العلاقات الثنائية التي تجمع بين الجزائر ونيبال.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة...

Sadr al-Din al-Qunawiصدر الدین القونویLahir1207Meninggal1274Konya, Seljuk RumEraZaman Kejayaan IslamKawasanAnatoliaAliransufismeMinat utamasufismemetafisikaepistemologi Dipengaruhi Ibnu ArabiIbnu Sina Memengaruhi RumiQuthbuddin asy-SyiraziFakhruddin al-Iraqi Bagian dari sebuah serial tentang IslamSufisme dan Tarekat Gagasan Abdal Ahwal Baqa Dzauq Fakir Fana Hakikat Ihsan Insan Kamil Karamah Kasyf Lataif Manzilah Makrifat Nafs Nur Iman Qutb Silsilah Salik Tazkiyatun-nafs W...

American astronaut (1932–2017) Paul WeitzBornPaul Joseph Weitz(1932-07-25)July 25, 1932Erie, Pennsylvania, U.S.DiedOctober 22, 2017(2017-10-22) (aged 85)Flagstaff, Arizona, U.S.EducationPennsylvania State University (BS)Naval Postgraduate School (MS)AwardsNASA Distinguished Service MedalAir MedalSpace careerNASA astronautRankCaptain, USNTime in space33d 1h 13mSelectionNASA Group 5 (1966)Total EVAs1Total EVA time1h 36mMissionsSkylab 2STS-6Mission insignia RetirementMay 1994 Paul Joseph...

Australian politician For the locomotive, see Victorian Railways S class. For the English cricketer, see Edward Henty (cricketer). Edward HentyBorn(1810-03-28)28 March 1810Tarring, Sussex, EnglandDied14 August 1878(1878-08-14) (aged 68)Melbourne, Colony of Victoria Edward Henty (28 March 1810 – 14 August 1878),[1] was a pioneer British colonist and is regarded as the first permanent settler in the Port Phillip district (later known as the colony of Victoria), Australia. Early l...

Vous lisez un « bon article » labellisé en 2013. Le roi Melishipak II de Babylone (1186–1172 av. J.-C.) présentant sa fille à la déesse Nanaya, détail d'un kudurru retrouvé à Suse. La religion de la Mésopotamie rassemble les pratiques et croyances religieuses polythéistes des divers peuples qui ont vécu en Mésopotamie pendant l'Antiquité, entre le IVe millénaire av. J.-C. et le début de notre ère : Sumériens, Akkadiens, Babyloniens, Assyriens pour...

German-born Hungarian locksmith master and factory owner Bust of Henrik Fazola, self-made, Foundry Museum, Budapest Henrik Fazola (German: Heinrich Fasola or Fassola) (1730 – 16 April 1779) was a German-born Hungarian locksmith master, a factory owner and one of the first representatives of industrial stock in Royal Hungary.[1] He lived in the city of Eger for some years, during which period he created his most famous wrought iron works. Furthermore, he found iron in the Bükk Mount...

2023 Philippine historical biographical film by Pepe Diokno GomBurZaTheatrical release posterDirected byPepe DioknoWritten by Rodolfo C. Vera Pepe Diokno Produced by Pauline Mangilog-Saltarin Ernestine Tamana Starring Dante Rivero Cedrick Juan Enchong Dee CinematographyCarlo Canlas MendozaEdited byBen TolentinoMusic byTeresa BarrozoProductioncompanies Jesuit Communications MQuest Ventures CMB Film Services Distributed by Solar Pictures[1] Release date December 25, 2023 ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of political parties in Sweden – news · newspapers · books · scholar · JSTOR (April 2023) (Learn how and when to remove this message) Politics of Sweden Basic Laws Instrument of Government Act of Succession Freedom of the Press Act Fundamental Law on Free...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Universidad de Texas en Austin» – noticias · libros · académico · imágenesEste aviso fue puesto el 1 de septiembre de 2018. University of Texas at Austin Universidad de Texas en Austin Sigla UTLema Disciplina praesidium civitatis«Educación, guardián de la sociedad»Tipo PúblicaFundación 1883LocalizaciónDirección 1 University Station, Austin, Texas 78...

American ballerina (1926–2021) Marjorie TallchiefTallchief in 1956BornMarjorie Louise Tall Chief(1926-10-19)October 19, 1926Denver, Colorado, U.S.DiedNovember 30, 2021(2021-11-30) (aged 95)Boca Raton, Florida, U.S.OccupationBallerinaSpouse George Skibine (m. 1947; died 1981)Children2CareerFormer groupsParis Opera Ballet Marjorie Tallchief (born Marjorie Louise Tall Chief; October 19, 1926 – November 30, 2021) was a...

La isla Programa de televisiónGénero Reality showDirigido por Luz AldamaPresentado por Pedro García AguadoPaís de origen EspañaIdioma(s) original(es) EspañolN.º de temporadas 2N.º de episodios 16ProducciónDuración 75 minutos (aprox.)Empresa(s) productora(s) Atresmedia TelevisiónShine IberiaLanzamientoMedio de difusión La SextaHorario Miércoles, a las 22h30 (T1)Jueves, a las 22h45 (T2)Fecha de lanzamiento 17 de mayo de 2017Enlaces externos Sitio web oficial Ver todos los créditos...

It has been suggested that Hurricane Isaias tornado outbreak be merged into this article. (Discuss) Proposed since May 2024. Category 1 Atlantic hurricane in 2020 Hurricane Isaias Hurricane Isaias intensifying near The Carolinas on August 3Meteorological historyFormedJuly 30, 2020ExtratropicalAugust 4DissipatedAugust 5, 2020Category 1 hurricane1-minute sustained (SSHWS/NWS)Highest winds90 mph (150 km/h)Lowest pressure986 mbar (hPa); 29.12 inHgOverall ef...

العلاقات الغينية اللبنانية غينيا لبنان غينيا لبنان تعديل مصدري - تعديل العلاقات الغينية اللبنانية هي العلاقات الثنائية التي تجمع بين غينيا ولبنان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة غينيا لبنا...

Long-ranged guns for land warfare Artilleryman redirects here. For the racehorse, see Artilleryman (horse). For other uses, see Artillery (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Artillery – news · newspapers · books · scholar · JSTOR (June 2022) (Learn how and when to remove this me...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) مركز الأفيهد الأفيهد الأفيهد تقسيم إداري البلد السعودية منطقة منطقة القصيم المسؤولون رئيس المركز نو�...

Résultats du Grand Prix de Monaco 1992, couru sur le circuit de Monaco le 31 mai 1992. Classement Ayrton Senna lors de sa cinquième victoire en Principauté Andrea Chiesa sur Fondmetal lors des essais du GP de Monaco 1992 Pos. No Pilote Écurie Tours Temps/Abandon Grille Points 1 1 Ayrton Senna McLaren-Honda 78 1 h 50 min 59 s 372(140,329 km/h) 3 10 2 5 Nigel Mansell Williams-Renault 78 + 0 s 215 1 6 3 6 Riccardo Patrese Williams-Renault 78 + 31 s 843 2 4 4 19 Michael Schumacher Benet...

VillecerfcomuneVillecerf – Veduta LocalizzazioneStato Francia Regione Île-de-France Dipartimento Senna e Marna ArrondissementFontainebleau CantoneMontereau-Fault-Yonne TerritorioCoordinate48°20′N 2°51′E48°20′N, 2°51′E (Villecerf) Superficie10,97 km² Abitanti792[1] (2009) Densità72,2 ab./km² Altre informazioniCod. postale77250 Fuso orarioUTC+1 Codice INSEE77501 CartografiaVillecerf Sito istituzionaleModifica dati su Wikidata · Manuale Villece...