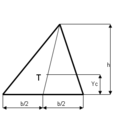
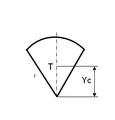
Težište
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Govind ...

Leipzig Panorama pusat kota Leipzig BenderaLambang kebesaranLetak Leipzig di distrik urban NegaraJermanNegara bagianSachsenWilayahLeipzigKreisdistrik urbanPemerintahan • Lord MayorBurkhard Jung (SPD)Luas • Total297,60 km2 (11,490 sq mi)Populasi (2013-12-31)[1] • Total531.582 • Kepadatan18/km2 (46/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos04001-04357Kode area telepon0341Pelat kendaraanLSitus webwww.leipzig.de Le...

Vanguard TV-3Satellite scientifique Le satellite Vanguard TV-3.Données générales Organisation U.S. Navy Constructeur Naval Research Laboratory (NRL) Programme IGY Vanguard Domaine Étude de la Terre Statut Mission terminée Base de lancement Cap Canaveral, LC-18A Lancement 6 décembre 1957 à16 h 44 min 34 s TU Lanceur Vanguard SLV Fin de mission 6 décembre 1957(détruit lors du lancement) Durée 2 secondes Identifiant COSPAR VAGT3 Caractéristiques techniques Masse au lancement 1,5 ...

Hitomi Yoshizawa吉澤 ひとみHitomi Yoshizawa tampil di Chibi Japan Expo, Prancis 2009, sebagai HangryLahir12 April 1985 (umur 39)Nama lainYossie, Yossui, Yossi, YocchanPekerjaan penyanyi aktris idola Peragawati Karier musikGenre Pop J-pop Tahun aktif2000–sekarangLabel Zetima Artis terkait Dream Morning Musume (2011-) Hangry & Angry (2008-) Morning Musume (2000-2007) Petitmoni Sakuragumi Ongaku Gatas 10-nin Matsuri Sexy 8 Venus Mousse 11Water H.P. All Stars Situs webHello!...

Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Muscolo retto femoraleSi mostrano i muscoli anteriori della coscia, fra cui il muscolo retto femoraleAnatomia del Gray(EN) Pagina 470 Originecrista iliaca, supra-acetabular groove e intertrochanteric line Inserzionebase of patella e tuberosità della tibia Antagonistamuscoli ischiocrurali Azioniflessione dell'...

Рыболовный ярус в собранном виде Я́русный лов — метод промышленного рыболовства, при котором для лова рыбы используются крючки с наживкой, прикреплённые к крючковому орудию лова — пелагическому или донному ярусу. Таким способом чаще всего ловят меч-рыбу, тунца, па...

American politician Charles Franklin SpragueMember of the U.S. House of Representativesfrom Massachusetts's 11th districtIn officeMarch 4, 1897 – March 3, 1901Preceded byWilliam F. DraperSucceeded bySamuel L. PowersMember of theMassachusetts State SenateIn officeJanuary 1895 - January 1897Preceded byFrancis William Kittredge[1]Succeeded byJoshua Bennett Holden[2]ConstituencyNinth Suffolk DistrictMember of the Massachusetts House of RepresentativesIn office1891-18...

House in New South Wales, AustraliaThe HermitageThe Hermitage, VaucluseThe HermitageLocation in Greater SydneyGeneral informationStatusCompletedTypeHouseArchitectural styleVictorian Rustic GothicLocation22 Vaucluse Road, Vaucluse, New South WalesCountryAustraliaCoordinates33°51′33″S 151°16′09″E / 33.8593°S 151.2693°E / -33.8593; 151.2693Construction started1870 (1870)Completed1878 (1878)Technical detailsMaterialSydney sandstoneDesign and construc...

PatlaborLogo Patlabor機動警察パトレイバー(Kidō Keisatsu Patoreibā)GenreKomedi, Drama, Mecha, Prosedural Polisi, Fiksi Ilmiah, Post-cyberpunk MangaPengarangHeadgearIlustratorMasami YūkiPenerbit ShogakukanDemografiShōnenTerbitApril 1988 – Juni 1994 Video animasi orisinalPatlabor: The Early DaysSutradaraMamoru OshiiSkenarioKazunori ItoStudio Studio Deen Novel ringanPengarangMichiko YokotePenerbitFujimi ShobōImprintFujimi Fantasia BunkoDemografiPriaTerbitOktober 1990 – Oktober ...

Cet article est une ébauche concernant un coureur cycliste belge. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Pour plus d’informations, voyez le projet cyclisme. Edgard SorgeloosEdgard Sorgeloos en 1952InformationsNaissance 14 décembre 1930DenderhautemDécès 12 novembre 2016 (à 85 ans)AudenardeNationalité belgeÉquipes professionnelles 08.1951-1952[n 1]Garin-Wolber1953Plume-Sport1954Peugeot-Dunlop1955-1956Elvé-Peugeot1957Peugeot-BP-Dunlop1958Elvé...

2005 single by Alicia KeysUnbreakableSingle by Alicia Keysfrom the album Unplugged ReleasedSeptember 6, 2005 (2005-09-06)RecordedJuly 4, 2005StudioBrooklyn Academy of Music (New York, New York)GenreR&BLength 4:34 (Album version) 4:14 (Radio edit) LabelJSongwriter(s) Alicia Keys Kanye West Harold Lilly Garry Glenn Producer(s)Alex ColettiWest (uncredited)[1]Alicia Keys singles chronology Karma (2004) Unbreakable (2005) Don't Give Up (Africa) (2005) Music videoUnbreaka...

الرابطة ثلاثية المركز ثنائية الإلكترون (يرمز لها 3c-2e) هي رابطة كيميائية ذات نقص إلكتروني، حيث تشترك ثلاث ذرات بزوج إلكتروني. يؤدي وجود ثلاث مدارات ذرّيّة إلى نشوء ثلاث مدارات جزيئية، أحدها رابط، والثاني غير رابط، في حين أن الثالث مضاد للترابط. يتموضع الإلكترونان في المدار �...

Luigi ZarconePersonal informationNationalityItalianBorn(1950-06-18)18 June 1950Villabate, ItalyDied9 June 2001(2001-06-09) (aged 50)Palermo, ItalySportCountry ItalySportAthleticsEvent(s)Middle distance runningLong distance runningClubG.S. Fiamme GialleAchievements and titlesPersonal bests 800 m: 1:49.6 (1976) 1500 m: 3:37.7 (1974) 3000 m: 7:47.54 (1977) 5000 m: 13:23.7 (1977) 10000 m: 28:02.3 (1977) Medal record Mediterranean Games 1979 Split 5000 metres 1979 Split 10000 metres Luigi Zar...

Racialized classification of people Blacks redirects here. For the color, see Black. For other uses, see Blacks (disambiguation). Black people African diaspora Americas Canada Caribbean Latin America United States Arab world Australia Europe India and Pakistan Iran Turkey Sri Lanka New Zealand Malaysia Indonesia Israel Japan Asia-Pacific Indigenous Australians Melanesians Negrito Papuans African-derived culture African-American art Black music Afro-American religion African-American culture H...

Lost opera by Scott Joplin 1903 Advertising poster for A Guest of Honor by Scott Joplin A Guest of Honor (ISJ 54)[1] is the first opera created by celebrated ragtime composer Scott Joplin. The opera had two acts, followed the model of grand opera,[2] and followed the events surrounding the 1901 White House dinner hosted by President Theodore Roosevelt for the civil rights leader and educator Booker T. Washington.[3] History Joplin is believed to have begun writing A Gu...

1648 – MDCXLVIII376 år sedan År1645 | 1646 | 164716481649 | 1650 | 1651 Årtionde1620-talet | 1630-talet 1640-talet1650-talet | 1660-talet Århundrade1500-talet 1600-talet1700-talet Årtusende1000-talet Året Födda | AvlidnaBildanden | Upplösningar Andra tideräkningar Gregorianska kalendern 1648 MDCXLVIII Ab urbe condita 2400 Armeniska kalendern 1097 ԹՎ ՌՂԷ Assyriska kalendern 6398 Bahaikalendern -196–-195 Bengali...

Стиль этого раздела неэнциклопедичен или нарушает нормы литературного русского языка. Статью следует исправить согласно стилистическим правилам Википедии. Пассивный дом (нем. Passivhaus, англ. passive house) — здание, основной особенностью которого является низкое энерго...

Il Ten Thousand Miles From Tip to Tip, manifesto politico statunitense datato 1898 Gingoismo o jingoismo (in lingua inglese jingoism) è una corrente sciovinista formatasi negli Stati Uniti d'America durante il XIX secolo. L'Oxford English Dictionary lo definisce come patriottismo estremista sotto forma di violenta politica estera[1]. Il gingoismo poneva la salvaguardia degli interessi della nazione e l'identità nazionale del paese come priorità vitali; veniva quindi adottata una po...

Village development committee in Narayani Zone, NepalPancha Kanya पञ्चकन्याVillage development committeeCountry NepalZoneNarayani ZoneDistrictChitwan DistrictPopulation (1991) • Total10,281Time zoneUTC+5:45 (Nepal Time) Pancha Kanya is a village development committee in Chitwan District in the Narayani Zone of southern Nepal. At the time of the 1991 Nepal census it had a population of 10,281 people living in 1,996 individual households.[...

Place in São Paulo, BrazilSanta Bárbara d'OesteMontage with images of Santa Bárbara d'Oeste FlagCoat of armsNickname: Pérola Açucareira (Sugar Pearl)Motto: Sancta Barbara Bene Juvante (Latin)Location in the São Paulo state.Santa Bárbara d'OesteCoordinates: 22°45′16″S 47°24′51″W / 22.75444°S 47.41417°W / -22.75444; -47.41417Country BrazilStateSão PauloMesoregionCampinasMicroregionCampinasGovernment • MayorRafael Piovezan (PV)Ar...