Проклятие размерности
|
Read other articles:

Tom Davies Manchester United Everton Tahun 2017Informasi pribadiNama lengkap Tom DaviesTanggal lahir 30 Juni 1998 (umur 25)Tempat lahir Liverpool, InggrisTinggi 180 cm (5 ft 11 in)Posisi bermain GelandangInformasi klubKlub saat ini Everton F.C.Nomor 26Karier senior*Tahun Tim Tampil (Gol)2015 – Everton F.C. 59 (4) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Tom Davies (lahir 30 Juni 1998) adalah seorang pemain sepak bola berkewarganegaraan Inggr...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2021) إيبون لايانا ديل ريو معلومات شخصية الميلاد 15 مايو 1976 (العمر 47 سنة)باساوري مواطنة إسبانيا الحياة العملية المهنة لاعبة تايكوندو اللغات الإسبانية الري...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2020. Nina GeorgeLahir(1973-08-30)30 Agustus 1973Bielefeld, JermanPekerjaanNovelis, Jurnalis Nina George (lahir 30 Agustus 1973) adalah seorang penulis Jerman, paling dikenal sebagai penulis The Little Paris Bookshop , buku terlaris internasional, yang telah...

Article principal : Cyclisme aux Jeux olympiques d'été de 2004. Cyclisme sur route aux Jeux olympiques d'été de 2004 Généralités Sport Cyclisme sur route Organisateur(s) UCI et le CIO Lieu(x) Athènes Date 18 août 2004 Palmarès Tenant du titre Viatcheslav Ekimov Vainqueur Viatcheslav Ekimov Deuxième Bobby Julich Troisième Michael Rogers Navigation Sydney 2000 Pékin 2008 modifier Le contre-la-montre masculin de cyclisme sur route, épreuve de cyclisme des Jeux olympiques d'ét...

Biografi ini memerlukan lebih banyak catatan kaki untuk pemastian. Bantulah untuk menambahkan referensi atau sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus, khususnya jika berpotensi memfitnah.Cari sumber: Pakubuwana XI – berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Pakubuwana XIꦥꦏꦸꦧꦸꦮꦤ�...

Teluk California (terang) Teluk California (juga dikenal sebagai Laut Cortez atau Laut Cortés; secara lokal dikenal dalam bahasa Spanyol sebagai Mar de Cortés atau Mar de Bermejo atau Golfo de California) merupakan badan air yang memisahkan Semenanjung Baja California dari daratan Meksiko. Berbatasan dengan negara bagian Baja California, Baja California Sur, Sonora, dan Sinaloa. Nama Teluk California mendominasi peta-peta dalam bahasa Inggris hari ini. Nama Laut Cortés dipilih oleh pendudu...

You can help expand this article with text translated from the corresponding article in Russian. (February 2014) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unreliable or l...

Pro Patria busteseGinnastica Segni distintivi Colori sociali Bianco, blu Dati societari Città Busto Arsizio Paese Italia Fondazione 1881 Presidente Rosario Vadalà Allenatore Scala Rino Palmarès La Società Ginnastica Pro Patria Bustese Sportiva, o Pro Patria Bustese, è una società di ginnastica di Busto Arsizio; vanta circa 30 atleti tra le sezioni agonistiche maschile e femminile, che competono nei campionati nazionali ed assoluti italiani. La sede sociale della Pro Patria Bustes...

Questa voce sull'argomento arbitri di calcio norvegesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Dag Vidar Hafsås Informazioni personali Arbitro di Calcio Sezione Kolstad Fotball Attività nazionale Anni Campionato Ruolo 2008- Eliteserien Arbitro Attività internazionale 2012-2018 UEFA Arbitro Esordio 5 luglio 2012 Dag Vidar Hafsås (Trondheim, 26 giugno 1973) è un arbitro di calcio norvegese. Carriera Helgerud arbitrò il primo incontro nell'...

Church near Antakya (Antioch), Turkey This article is about the church building in present Turkey. For the church in the Vatican City, see St. Peter's Basilica. For other uses, see St. Peter's (disambiguation) and St. Peter's Church (disambiguation).This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Church of Saint Peter – news �...

国民阵线Barisan NasionalNational Frontباريسن ناسيونلபாரிசான் நேசனல்国民阵线标志简称国阵,BN主席阿末扎希总秘书赞比里署理主席莫哈末哈山总财政希山慕丁副主席魏家祥维纳斯瓦兰佐瑟古律创始人阿都拉萨成立1973年1月1日 (1973-01-01)[1]设立1974年7月1日 (1974-07-01)前身 联盟总部 马来西亚 吉隆坡 50480 秋傑区敦依斯迈路太子世贸中心(英�...

Questa voce sull'argomento calciatori ghanesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. George Alhassan Nazionalità Ghana Altezza 188 cm Peso 77 kg Calcio Ruolo Attaccante Termine carriera 1992 CarrieraSquadre di club1 1977-1982 Great Olympics? (?)1982-1984 FC 105 Libreville? (?)1984 Hyundai Horang-i11 (4)1985-1990 Great Olympics? (?)1990-1992 Berchem? (?)Nazionale...

Indian cricket team in Zimbabwe in 1998 India ZimbabweDates 26 September – 10 October 1998Captains Mohammad Azharuddin Alistair CampbellTest seriesResult Zimbabwe won the 1-match series 1–0Most runs Rahul Dravid (162) Gavin Rennie (131)Most wickets Anil Kumble (7) Henry Olonga (6)One Day International seriesResults India won the 3-match series 2–1Most runs Sourav Ganguly (158)Sachin Tendulkar (158) Alistair Campbell (131)Most wickets Ajit Agarkar (6) Heath Streak (4)Pl...

Hollywood Records, Inc.Perusahaan indukDisney Music GroupDidirikan1989; 35 tahun lalu (1989)PendiriMichael EisnerDistributorUniversal Music GroupGenreBeragam; sebagian besar popAsal negaraAmerika SerikatLokasi500 S. Buena Vista StreetBurbank, CaliforniaSitus webhollywoodrecords.com Hollywood Records adalah sebuah perusahaan rekaman milik The Walt Disney Company yang didirikan pada 1989. Awalnya didistribusikan oleh Elektra Records di Amerika Serikat dan Kanada, berganti ke PolyGram pada ...

City in West Bengal, India This article is about the city in India. For other uses, see Jalpaiguri (disambiguation). City in West Bengal, IndiaJalpaiguriCity From top, left-to-right: Kanchenjunga from outskirts of Jalpaiguri city,Jalpaiguri Rajbari Gate, Raikat Temple JalpaiguriLocation in West Bengal, IndiaShow map of West BengalJalpaiguriJalpaiguri (India)Show map of IndiaCoordinates: 26°31′N 88°44′E / 26.52°N 88.73°E / 26.52; 88.73Country IndiaState Wes...
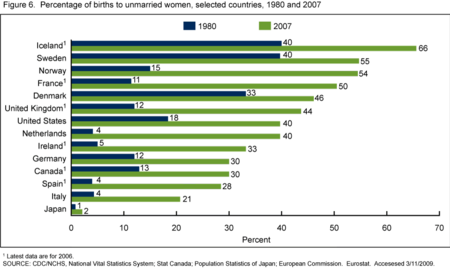
Sexual activity before marriage This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Premarital sex – news · newspapers · books · scholar · JSTOR (December 2018) (Learn how and when to remove this message) Percentage of births to unmarried women, selected countries, 1980 and 2007[1] Premarital sex is sexu...

British film director and writer (1954–2008) Anthony MinghellaCBEMinghella in 2004Born(1954-01-06)6 January 1954Ryde, Isle of Wight, EnglandDied18 March 2008(2008-03-18) (aged 54)London, EnglandAlma materUniversity of HullOccupationsPlaywrightdirectorscreenwriterYears active1975–2008Spouses Yvonne Miller (divorced) Carolyn Choa (m. 1985) Children2, including MaxRelativesDominic Minghella (brother) Anthony Minghella, C...

1967 novel by Thomas Keneally Bring Larks and Heroes First editionAuthorThomas KeneallyLanguageEnglishPublisherCassell, AustraliaPublication date1967Publication placeAustraliaMedia typePrint (Hardback & Paperback)Pages247 ppISBN0-7251-0060-5OCLC27549590Preceded byThe Fear Followed byThree Cheers for the Paraclete Bring Larks and Heroes is a 1967 novel by Australian author Thomas Keneally[1] which won the Miles Franklin Award in 1967.[2] Plot summa...

Voce principale: Associazione Calcio Prato. Associazione Calcio PratoStagione 1979-1980Sport calcio Squadra Prato Allenatore Giovanni Meregalli Presidente Andrea Toccafondi Serie C21º posto nel girone A. Promosso in Serie C1. Maggiori presenzeCampionato: Bertocco, Cecconi (32) Miglior marcatoreCampionato: Biloni (13) 1978-1979 1980-1981 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Calcio Prato nelle competizioni ufficiali del...

American actor (1884–1927) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hughie Mack – news · newspapers · books · scholar · JSTOR (May 2019) (Learn how and when to remove this message) Hughie MackBorn(1884-11-26)November 26, 1884Brooklyn, New YorkDiedOctober 13, 1927(1927-10-13) (aged 42)Santa Moni...






