Wielomian nieprzywiedlny
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Aisyiyah – berita · surat kabar · buku · cendekiawan · JSTOR (Oktober 2013) Artikel ini menggunakan bahan sumber yang berasal dari blog atau situs pribadi yang dapat tidak sesuai dengan kebijakan pemastian da...

العلاقات الوسط أفريقية الليتوانية جمهورية أفريقيا الوسطى ليتوانيا جمهورية أفريقيا الوسطى ليتوانيا تعديل مصدري - تعديل العلاقات الوسط أفريقية الليتوانية هي العلاقات الثنائية التي تجمع بين جمهورية أفريقيا الوسطى وليتوانيا.[1][2][3][4][5] ...

Monnaie de Vuk Branković. Vuk Branković (en serbe cyrillique Вук Бранковић), était un seigneur médiéval serbe. Fils de Branko Mladenović, qui était le gouverneur de Ohrid et un des conseillers de Stefan Uroš V dit le faible. Il apparaît dans l'histoire vers 1370, en tant que seigneur du Kosovo de Priština, Vučitrn et Zvečan. Skopje est sous son autorité à partir de 1378. Vuk était le beau-fils du Prince Lazar Hrebeljanović, il avait épousé en 1371 sa fille Mara. ...

Keuskupan PittsburghDioecesis PittsburgensisKatolik LokasiNegaraAmerika SerikatWilayahAllegheny, Beaver, Butler, Greene, Lawrence, dan WashingtonProvinsi gerejawiProvinsi PhiladelphiaKantor pusat111 Boulevard of the Allies Pittsburgh, PA 15222StatistikLuas3.786 sq mi (9.810 km2)Populasi- Total- Katolik(per 2016)1.915.363632,138 (33%)Paroki188InformasiDenominasiKatolik RomaRitusRitus LatinPendirian11 Agustus 1843KatedralKatedral Santo PaulusPelindungDikandung...

Перевёрнутая кратка снизу ◌̯ Изображение ◄ ◌̫ ◌̬ ◌̭ ◌̮ ◌̯ ◌̰ ◌̱ ◌̲ ◌̳ ► Характеристики Название combining inverted breve below Юникод U+032F HTML-код ̯ или ̯ UTF-16 0x32F URL-код %CC%AF Перевёрнутая кратка снизу (◌̯) — диакритический знак, используемый в МФА. Содержание 1 Ис�...

Novyanto Widadi Kepala Pusat Penelitian dan Pengembangan Transportasi Udara Kepala Pusat Kebijakan Penerbangan (Validasi Organisasi)PetahanaMulai menjabat 20 Desember 2019Kepala Badan LitbangUmiyatun Hayati (2020–2021)Umar Aris (2021–sekarang)PendahuluM. AlwiPenggantiPetahanaSekolah Tinggi Penerbangan Indonesia Curug Ketua Sekolah Tinggi Penerbangan IndonesiaMasa jabatan2 November 2016 – 12 Desember 2019PendahuluYudi Sari SitompulPenggantiAviriantoKomandan Skadron Udara 4Ma...
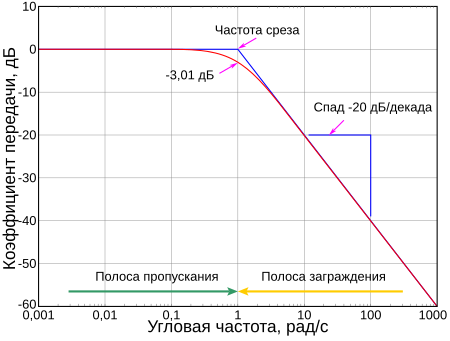
Коэффицие́нт переда́чи (также коэффициент преобразова́ния, крутизна преобразова́ния) — отношение приращения некоторой физической величины на выходе некоторой системы Δ A o {\displaystyle \Delta A_{o}} к вызвавшему это приращение, изменению подаваемой на вход величины данн...

Pour les articles homonymes, voir Lucernaire. Lucernaire Façade rue Notre-Dame-des-Champs Données clés Lieu Paris, France Coordonnées 48° 50′ 39″ nord, 2° 19′ 50″ est Inauguration 1968 Nb. de salles 6 Gestionnaire Éditions L'Harmattan Direction Benoît Lavigne et Karine Letellier[1] Site web www.lucernaire.fr modifier Le Lucernaire, Centre national d’art et d’essai, est un centre culturel à Paris, mêlant notamment théâtre, cinéma et photo...

Come leggere il tassoboxSiphoviridae Classificazione dei virus Dominio Duplodnaviria Gruppo Gruppo I (Virus a dsDNA) Ordine Caudovirales Famiglia Siphoviridae Generi c2-like viruses L5-like viruses Lambda-like viruses N15-like viruses PhiC31-like viruses PsiM1-like viruses SPbeta-like viruses T1-like viruses T5-like viruses I Siphoviridae sono una famiglia di virus facente parte dell'ordine Caudovirales, nel gruppo I della Classificazione di Baltimore[1]. Di questa famiglia fa parte ...

قراصنة الكاريبي: الرجال الأموات لا يحكون حكاياتPirates of the Caribbean: Dead Men Tell No Tales (بالإنجليزية) الشعارملصق الفيلممعلومات عامةالتصنيف فيلم ثلاثي الأبعاد الصنف الفني القائمة ... فيلم صيد كنوز — فيلم فنتازيا — فيلم عجرفة — فيلم قراصنة — فيلم كوميدي الموضوع قرصنة بحرية تاريخ الص...

نوكيا 206معلومات عامةالنوع هاتف محمول الصانع نوكياعائلة المنتج نوكيا ثلاثى الأرقامموقع الويب http://www.nokia.com/global/الوظائفالشاشة إل سي دي 320× 240الكاميرا 1.3 ميجابكسلالخصائصسعة التخزين 64 ميجابايتشريحة ذاكرة تصل إلى 32 جيجابايتالبطارية 1110 م.أ/سالاتصال بلوتوثالقياساتالأبعاد 116.0 ملي...

United States lobbying law Honest Leadership and Open Government Act of 2007Other short titlesCommission to Strengthen Confidence in Congress Act of 2007Congressional Pension Accountability ActLegislative Transparency and Accountability Act of 2007Long titleAn Act to provide greater transparency in the legislative process.Acronyms (colloquial)HLOGAEnacted bythe 110th United States CongressEffectiveSeptember 14, 2007CitationsPublic law110-81Statutes at Large121 Stat. 735Codifica...

Wappen Deutschlandkarte ? Basisdaten Koordinaten: 53° 39′ N, 12° 50′ O53.6512.83333333333338Koordinaten: 53° 39′ N, 12° 50′ O Bundesland: Mecklenburg-Vorpommern Landkreis: Mecklenburgische Seenplatte Amt: Stavenhagen Höhe: 38 m ü. NHN Fläche: 19,03 km2 Einwohner: 267 (31. Dez. 2022)[1] Bevölkerungsdichte: 14 Einwohner je km2 Postleitzahl: 17153 Vorwahl: 039951 Kfz-Kennzeichen: MSE, AT, DM, MC, M...

Criminal punishment Life sentence redirects here. For other uses, see Life Sentence (disambiguation). Life term redirects here. For lifelong terms of office, see Life tenure. Not to be confused with Indefinite imprisonment. Criminal procedure Criminal trials and convictions Rights of the accused Fair trial Pre-trial Speedy trial Jury trial Counsel Presumption of innocence Exclusionary rule1 Self-incrimination Double jeopardy2 Bail Appeal Verdict Conviction Acquittal Not proven3 Directed verdi...

Internment camps set up by the British during the Malayan Emergency For other places named Kampung Baru, see Kampung Baru (disambiguation). Gombak New Village Loke Yew New Village in Kuala LumpurPart of a series on the History of Malaysia Prehistoric Malaysia Paleolithic Lenggong Valley c. 2,000,0000 BCE Mansuli Valley235,000 BCE Mesolithic Niah cultures 65,000–40,000 BCE Neolithic Bewah man/woman 16,000 BCE Perak man/woman 11,000–200 BCE Neolit...

Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Percentuali di grassi saturi, monoinsaturi e polinsaturi contenuti negli alimenti. La sindrome di Burr o sindrome da carenza di acidi grassi essenziali è un disturbo polimorfo prodotto dalla carenza di acidi grassi essenziali (AGE) nell'organismo. Nella lingua inglese gli AGE sono conosciuti come EFA (Essenti...

Italian sculptor Angelo Gabriello PiòBorn1690BolognaDied1770BolognaNationalityBologneseOccupationSculptor Angelo Gabriello Piò (Bologna, 1690- Bologna, 1770) was an Italian sculptor, active in Bologna in a Rococo style. Life In Bologna, he studied from 1711 to 1712 under Andrea Ferreri (1673–1744) .[1] He was also a pupil of Giuseppe Maria Mazza.[2] After 1718 he studied in Rome under Camillo Rusconi (1658-1728).[1] In 1721 Piò became a member of the Accademia Cle...

علي فخر الدين معلومات شخصية الميلاد 3 أبريل 1983 (العمر 41 سنة)لبنان الجنسية لبنان الطول 80 بوصة الوزن 210 رطل الحياة العملية المهنة لاعب كرة سلة[1] الرياضة كرة السلة[2] تعديل مصدري - تعديل علي فخر الدين، ولد في لبنان في 3 نيسان، 1983، لاعب كرة السلة اللبنا�...

Pour les articles homonymes, voir Aube. Aube L'Aube à la sortie de Bar-sur-Aube. Cours de l'Aube (carte interactive). Caractéristiques Longueur 248,9 km [1] Bassin 4 660 km2 [1] Bassin collecteur Seine Débit moyen 41 m3/s (Marcilly-sur-Seine) [note 1] Régime Pluvial océanique Cours Source Plateau de Langres · Localisation Praslay · Altitude 379 m · Coordonnées 47° 45′ 40″ N, 5° 07′ 30″ E Confluence Seine · Localisatio...

1806 dissolution of the Holy Roman Empire following Francis II's abdication Dissolution of the Holy Roman EmpireThe final stage of the Holy Roman Empire, before the Napoleonic Wars.Date6 August 1806; 218 years ago (1806-08-06)Location Holy Roman EmpireParticipantsFrancis II, Holy Roman EmperorThe Princes of the Holy Roman EmpireOutcomeDissolution of the Holy Roman Empire; succeeded chiefly by the short-lived Napoleonic Confederation of the Rhine and then the Habsburg-Lo...
















