Równanie czwartego stopnia
|
Read other articles:

Daanbantayan Munisipalitas di Filipina Tempat categoria:Articles mancats de coordenades Negara berdaulatFilipinaRegion di FilipinaVisayas TengahProvinsi di FilipinaCebu NegaraFilipina Pembagian administratifAguho Bagay (en) Bakhawan (en) Bateria (en) Bitoon (en) Calape (en) Carnaza Dalingding (en) Lanao (en) Logon Malbago (en) Malingin (en) Maya (en) Pajo (en) Paypay (en) Poblacion (en) Talisay (en) Tapilon (en) Tinubdan (en) Tominjao (en) PendudukTotal93.502 (2020 )Tempat tinggal22.289...

Television channel TV ChileCountryChileBroadcast areaWorldwideNetworkTelevisión Nacional de ChileProgrammingLanguage(s)SpanishPicture format1080i HDTV(downscaled to 480i/576i for the SD feed)OwnershipOwnerTelevisión Nacional de ChileHistoryLaunched1989; 35 years ago (1989)Former namesTelevisión Nacional de Chile(1989-1992)Televisión Nacional de Chile Imagen Internacional(1992-1995)LinksWebsitehttp://www.tvchile.cl TV Chile is a Chilean pay television network that airs fr...

Kompi Zeni Penjinak Bahan Peledak(Kizi Jihandak)Lambang Kizi Jihandak PusziadAktif22 April 1986Negara IndonesiaCabangTNI Angkatan DaratTipe unitSatuan Bantuan tempurBagian dariPusat Zeni Angkatan DaratMarkasJalan Raya Lenteng Agung, Jagakarsa, Jakarta SelatanJulukanKizi Jihandak/SDSMotoSura Dharma SantikaSitus webwww.ditzi-tniad.mil.id Kompi Zeni Penjinak Bahan Peledak Ditzi TNI-AD disingkat Kizi Jihandak/Sura Dharma Santika Adalah Kompi Berdiri Sendiri (BS) yang dibentuk pada 22 April 1...

2006 American filmFast Food NationTheatrical release posterDirected byRichard LinklaterScreenplay byRichard LinklaterEric SchlosserBased onFast Food Nationby Eric SchlosserProduced byJeremy ThomasMalcolm McLarenStarringPatricia ArquetteLuis GuzmánEthan HawkeAshley JohnsonGreg KinnearKris KristoffersonCatalina Sandino MorenoAna Claudia TalancónWilmer ValderramaBobby CannavalePaul DanoAaron HimelsteinCinematographyLee DanielEdited bySandra AdairMusic byFriends of Dean MartinezProductioncompa...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Right-wing American magazine The New AmericanOctober 17, 2022 coverEditorGary BenoitCategoriesEditorial MagazineFrequencySemimonthlyPublisherDennis BehreandtTotal circulation(2021)20,194[1]First issueSeptember 30, 1985CompanyAmerican Opinion PublishingCountryUnited StatesBased inAppleton, WisconsinLanguageEnglishWebsitethenewamerican.com ISSN0885-6540 This article is part of a series onConservatismin the United States Schools Compassionate Fiscal Fusion Libertarian Moderate Movement N...

List of different types of entertainment This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of genres – news · newspapers · books · scholar · JSTOR (Aug...

Mountain in Washington (state), United States Old DesolateOld Desolate's south peakHighest pointElevation7,137 ft (2,175 m)[1]Prominence1,017 ft (310 m)[1]Parent peakBurroughs Mountain (7,828 ft)[2]Isolation2.38 mi (3.83 km)[2]Coordinates46°55′30″N 121°45′01″W / 46.925114°N 121.750188°W / 46.925114; -121.750188GeographyOld DesolateLocation of Old Desolate in WashingtonShow map of Washington ...

Propriétés des systèmes isolés, fermés et ouverts dans l'échange d'énergie et de matière. Un système isolé, par opposition à un système ouvert, est un système physique qui n'interagit pas avec ses environnements. On dit d’un système qu’il est isolé s’il n'échange ni matière, ni chaleur, ni travail avec l'extérieur (paroi adiabatique et indéformable) – un système fermé peut échanger de la chaleur ou du travail avec l'extérieur, mais pas de la matière. Ce systèm...

Сифран (от порт. cifrão от лат. cifra — цифра, португальское произношение: [siˈfɾɐ̃w̃] (слушать)о файле) — типографский символ, который первоначально использовался в португалоязычных рукописях в качестве разделителя разрядов и напоминал символ доллара ($). В наст�...

Sekretaris Jenderal Organisasi Kesatuan Afrika adalah jabatan yang dipegang oleh pemimpin Sekretariat Organisasi Kesatuan Afrika.[1] Daftar # Foto Ketua Mulaimenjabat Selesaimenjabat Negara Kawasan – Kifle Wodajo (sementara) 25 Mei 1963 21 Juli 1964 Ethiopia Afrika Timur 1 Diallo Telli 21 Juli 1964 15 Juni 1972 Guinea Afrika Barat 2 Nzo Ekangaki 15 Juni 1972 16 Juni 1974 Kamerun Afrika Tengah 3 William Eteki 16 Juni 1974 21 Juli 1978 Kamerun Afrika Tengah 4 E...

City in Massachusetts, United StatesNorth AdamsCityMain Street SealMotto: We Hold the Western GatewayLocation in Berkshire County and the state of Massachusetts.North AdamsLocation in the United StatesCoordinates: 42°42′N 73°7′W / 42.700°N 73.117°W / 42.700; -73.117CountryUnited StatesCommonwealthMassachusettsCountyBerkshireSettled1745Incorporated1878 (Town)Incorporated1895 (City)Government • TypeMayor-council city • MayorJennifer ...
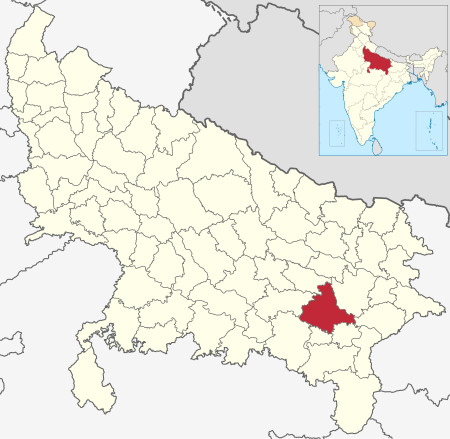
Lokasi Jaunpur di Uttar Pradesh Jaunpur (जौनपुर) (جون پور) adalah sebuah kota di Uttar Pradesh India. Jaunpur terletak di barat laut dari Varanasi di timur Uttar Pradesh. Sejarah pendirian kota jaunpur ini pada tahun 1388 selama pemerintahan Tughlaq, ketika itu sebagai pusat utama kota berbahasa Urdu dan pengetahuan dan budaya Sufi. Lokasi Jaunpur terletak di garis bujur 25 ° 46 'LU dan 82 ° 44' E. Jaunpur berbatasan dengan Allahabad, Sant Ravidas Nagar dan Varanasi di Sel...

Disambiguazione – Se stai cercando altri significati, vedi Division Nationale (disambigua). Division NationaleAltri nomiBGL Ligue Sport Calcio TipoClub FederazioneFLF Paese Lussemburgo OrganizzatoreFederazione calcistica del Lussemburgo TitoloCampione di Lussemburgo Partecipanti16 squadre [1] FormulaGirone all'italiana Retrocessione inÉirepromotioun StoriaFondazione1909 Numero edizioni107 Detentore Differdange 03 Record vittorie Jeunesse Esch (28) Ultima edizioneDiv...

العلاقات الإندونيسية الكورية الجنوبية إندونيسيا كوريا الجنوبية إندونيسيا كوريا الجنوبية تعديل مصدري - تعديل العلاقات الإندونيسية الكورية الجنوبية هي العلاقات الثنائية التي تجمع بين إندونيسيا وكوريا الجنوبية.[1][2][3][4][5] مقارنة بين ا�...

American television series Playhouse 90GenreAnthologyWritten byRobert Alan AurthurJames P. CavanaghHorton FooteJohn GayWilliam GibsonFrank D. GilroyArthur HaileyA.E. HotchnerErnest KinoyLoring MandelDon M. MankiewiczAbby MannJ. P. MillerPaul MonashTad MoselReginald RoseRod SerlingDavid ShawAaron SpellingLeslie StevensMalvin WaldDirected byJohn BrahmJames B. ClarkFielder CookVincent J. DonehueJohn FrankenheimerDavid GreeneGeorge Roy HillArthur HillerHerbert HirschmanBuzz KulikDelbert MannBurge...

9th century work of Byzantine Patriarch Photius Cover of Bibliotheca The Bibliotheca (Greek: Βιβλιοθήκη) or Myriobiblos (Μυριόβιβλος, Ten Thousand Books) was a ninth-century work of Byzantine Patriarch of Constantinople Photius, dedicated to his brother and composed of 279 reviews of books which he had read. Overview Bibliotheca was not meant to be used as a reference work, but was widely used as such in the 9th century, and is one of the first Byzantine works that could ...

This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (January 2015) (Learn how and when to remove this message) LassoLassoSoft Inc. LogoParadigmMulti-paradigm: structured object-oriented (multi-dis), imperative: procedural, concurrent, exp-oriented, Meta: reflectiveDesigned byKyle JessupDeveloperLassoSoft Inc.Fir...

Baseball park in Jacksonville, Florida 121 Financial BallparkThe home plate entranceFormer namesJacksonville Baseball Park (planning/construction)Baseball Grounds of Jacksonville (2003–2014, 2017–2019) [1]Community First Park (2015–16)Location301 A. Philip Randolph BoulevardJacksonville, FloridaUnited StatesCoordinates30°19′30″N 81°38′35″W / 30.324968°N 81.643069°W / 30.324968; -81.643069OwnerCity of JacksonvilleOperatorASM GlobalCapacity11,00...

Les droits des femmes sont des droits revendiqués pour les femmes dans de nombreuses sociétés à travers le monde, qui constituent la base du mouvement pour les droits des femmes du XIXe siècle ainsi que le combat des mouvements féministes depuis le XXe siècle. Dans certains pays, ces droits sont institutionnalisés ou soutenus par la loi, la coutume locale et le comportement, tandis que dans d'autres pays, ils peuvent être ignorés, réprimés ou supprimés. Ils diffèrent ...


















































































![{\displaystyle =\left[\left(2u-t_{1}\right)^{2}-\left(v_{1}+w_{1}\right)^{2}\right]\left[\left(2u+t_{1}\right)^{2}-\left(v_{1}-w_{1}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50e8c711becef24f94eff0fe65e0c9e22862292c)
























