Stowarzyszenie Gmin i Powiatów Małopolski
|
Read other articles:

SosiologiDiagram Analisis Jejaring Sosial Portal Teori dan Sejarah Positivisme · Antipositivisme Fungsionalisme · Teori konflik Strukturalisme · Interaksi simbolik · Jarak menengah · Matematis Teori kritis · Sosialisasi Struktur dan agen Metode penelitian Kuantitatif · Kualitatif Komputasional · Etnografi Topik dan Cabang agama · budaya · demografi ekonomi · hukum · ilmu · industri internet · jejaring sosial · jenis kelamin kejahatan · kelas · keluarga kesehatan · kota...

Pour les articles homonymes, voir Soufflet. Jacques Soufflet Fonctions Ministre des Armées 28 mai 1974 – 21 janvier 1975(7 mois et 24 jours) Président Valéry Giscard d'Estaing Premier ministre Jacques Chirac Gouvernement Jacques Chirac I Prédécesseur Robert Galley Successeur Yvon Bourges Sénateur français 27 avril 1959 – 28 juin 1974(15 ans, 2 mois et 1 jour) Élection 26 avril 1959 Réélection 22 septembre 1968 Circonscription Seine-et-Oise (1959-1968)Yv...

محمد أباد عندليب تقسيم إداري البلد إيران [1] التقسيم الأعلى منطقة بايين ولايت الريفية خصائص جغرافية إحداثيات 35°13′57″N 58°22′38″E / 35.2325°N 58.377222222222°E / 35.2325; 58.377222222222 الارتفاع 1007 متر السكان التعداد السكاني 62 (إحصاء السكان) (2006) الرمز الجغرافي 4...

Гологорлый звонарь Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:�...

Ketika Cinta Bertasbih 2SutradaraChaerul UmamProduser Mitzy Christina Cindy Christina SkenarioImam TantowiBerdasarkanKetika Cinta Bertasbiholeh Habiburrahman El ShirazyPemeran Kholidi Asadil Alam Oki Setiana Dewi Alice Sofie Norin Andi Arsyil Rahman Meyda Sefira Penata musik Anto Hoed Melly Goeslaw SinematograferRudy KurwetPenyuntingRizal BasriPerusahaanproduksiSinemArt PicturesTanggal rilis 17 September 2009 (2009-09-17) (Indonesia) Durasi120 menitNegaraIndonesiaBahasaBahasa I...

Questa voce sull'argomento contee dell'Oklahoma è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di Tulsacontea Contea di Tulsa – Veduta LocalizzazioneStato Stati Uniti Stato federato Oklahoma AmministrazioneCapoluogoTulsa Data di istituzione1905 TerritorioCoordinatedel capoluogo36°07′12″N 95°56′24″W / 36.12°N 95.94°W36.12; -95.94 (Contea di Tulsa)Coordinate: 36°07′12″N 95°56′24″W / &#x...

You can help expand this article with text translated from the corresponding article in Japanese. Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a topic to this template: there are already 3,701 arti...

1900 siege in Peking during the Boxer Rebellion Siege of the International LegationsPart of the Boxer RebellionI'll Try, Sir!: American troops scale the walls of Peking, with the Fox Tower in flames. Depicted is trumpeter Calvin Titus who first climbed the wall and was later awarded the Medal of Honor.DateJune 20 – August 14, 1900 (1 month, 3 weeks and 4 days)LocationBeijing, China39°54′11″N 116°24′06″E / 39.90306°N 116.40167°E / 39.90306; ...

US Open 2013 Sport Tennis Data 26 agosto – 9 settembre Edizione 133a Categoria Grande Slam (ITF) Superficie Cemento Località New York, USA Impianto USTA Billie Jean King National Tennis Center, Flushing Meadows Campioni Singolare maschile Rafael Nadal Singolare femminile Serena Williams Doppio maschile Leander Paes / Radek Štěpánek Doppio femminile Andrea Hlaváčková / Lucie Hradecká Doppio misto Andrea Hlaváčková / Maks Mirny Singolare ragazzi Borna Ćorić Singolare ragazze Ana...

Zwei kleine Italiener Cornelia Froboess interprétant Zwei kleine Italiener lors du Concours Eurovision de la chanson 1962 à Luxembourg. Chanson de Cornelia Froboess auConcours Eurovision de la chanson 1962 Sortie 1962 Langue Allemand Genre Schlager, pop, variété Auteur George Buschor Compositeur Christian Bruhn Chansons représentant l'Allemagne au Concours Eurovision de la chanson Einmal sehen wir uns wieder(1961) Marcel(1963)modifier Zwei kleine Italiener (en français : «&#...

Населённый пунктХанькоу Церковь в честь святого князя Александра Невского 30°34′52″ с. ш. 114°16′21″ в. д.HGЯO Страна Китайская республика Режим Ван Цзинвэя Реформированное правительство Китайской Республики Китайская республика империя Цин История...

1906 four-masted barque This article is about a Danish sailing ship. For other ships named Viking, see Viking (disambiguation) § Ships. You can help expand this article with text translated from the corresponding article in Swedish. (March 2024) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accur...

2023 soundtrack album by Ludwig Göransson Oppenheimer (Original Motion Picture Soundtrack)Soundtrack album by Ludwig GöranssonReleasedJuly 21, 2023 (2023-07-21)StudioEastwood Scoring Stage, Burbank, CaliforniaGenreOrchestralcontemporary classicalfilm scoreLength94:42LabelBack LotProducerLudwig GöranssonLudwig Göransson film score chronology Black Panther: Wakanda Forever (Original Score)(2022) Oppenheimer (Original Motion Picture Soundtrack)(2023) Christopher Nolan fil...

Indian playback singer This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2020) (Learn how and when to remove this message) Vaishali SamantSamant in 2014Born (1974-04-25) 25 April 1974 (age 50)Maharashtra, IndiaOccupation(s)Singer, composer Vaishali Samant is an Indian music composer, lyricist and playback singer who is popularly known for her work ...

Katedral Gatchina Eparki Gatchina adalah sebuah eparki Gereja Ortodoks Rusia yang terletak di Gatchina, Federasi Rusia. Eparki tersebut didirikan pada 2013.[1] Referensi ^ http://www.patriarchia.ru/db/text/2844846.html lbsKeuskupan Gereja Ortodoks RusiaPatriark MoskwaEparki di Rusia Abakan dan Khakassia Akhtubinsk Alapayevsk Alatyr Alexdanrov Almetyevsk Amur Anadyr Ardatov Arkhangelsk Armavir Arsenyev Astrakhan Balashov Barnaul Barysh Belgorod Belyov Bezhetsk Birobidzhan Birsk Biysk B...

كولبيرتسون الإحداثيات 48°08′50″N 104°31′02″W / 48.147222222222°N 104.51722222222°W / 48.147222222222; -104.51722222222 [1] تاريخ التأسيس 1887 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة روزفلت خصائص جغرافية المساحة 1.338815 كيلومتر مربع1.55243 كيلومتر مربع...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: extensive unreferenced information. Please help improve this article if you can. (February 2016) (Learn how and when to remove this message) This article needs additional citations for verification. Please help improve this article by adding cita...

SK Inc.Nama asli에스케이 주식회사SebelumnyaSK HoldingsJenisPublikKode emitenTemplat:KRXIndustriKonglomerat Jasa teknologi informasiDidirikan1991; 33 tahun lalu (1991)KantorpusatSeoul, Korea SelatanTokohkunciChey Tae-won (Chairman & CEO) Jang Dong-hyun (Presiden & CEO) Park Sung-ha (Presiden & CEO)AnakusahaSK Innovation SK TelecomSitus webwww.sk-inc.com/en/Catatan kaki / referensi[1] SK Inc. (Hangul: 에스케이 주식회사) adalah sebuah perusa...
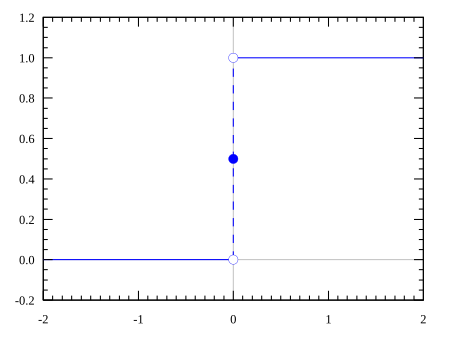
In matematica, il limite di una funzione in un punto di accumulazione[1] per il suo dominio esprime la quantità a cui tende il valore assunto dalla funzione all'avvicinarsi del suo argomento a quel punto. Indicando con f ( x ) {\displaystyle f(x)} la funzione e con x 0 {\displaystyle x_{0}} il punto di accumulazione, il limite viene indicato con: lim x → x 0 f ( x ) {\displaystyle \lim _{x\to x_{0}}f(x)} e si legge limite di f ( x ) {\displaystyle f(x)} per x {\displaystyle x}...

Institutional corruption in the country Political corruption Forms and concepts Bribery Cronyism Economics of corruption Electoral fraud Elite capture Influence peddling Kleptocracy Mafia state Nepotism Pyrrhic defeat theory Slush fund Simony State capture State-corporate crime Throffer Anti-corruption International Anti-Corruption Court Group of States Against Corruption International Anti-Corruption Academy International Anti-Corruption Day United Nations Convention against Corruption Corru...