二階述語論理
|
Read other articles:

Dorothy BernardBernard, c. 1915LahirNora Dorothy Bernard(1890-06-25)25 Juni 1890Port ElizabethMeninggal14 Desember 1955(1955-12-14) (umur 65)Hollywood, California, A.S.PekerjaanAktrisTahun aktif1908-1956 Dorothy Bernard (25 Juni 1890 – 14 Desember 1955) adalah seorang aktris Amerika dari era film bisu. Dia muncul di 87 film antara 1908 dan 1956. Dia lahir Nora Dorothy Bernard di Port Elizabeth, British Cape Colony, sekarang bagian dari Afrika Selatan, dari pasangan ...

Burung-sepatu kecil Microparra capensis BotswanaStatus konservasiRisiko rendahIUCN22693536 TaksonomiKerajaanAnimaliaFilumChordataKelasAvesOrdoCharadriiformesFamiliJacanidaeGenusMicroparraSpesiesMicroparra capensis Smith, 1839 lbs Burung-sepatu kecil ( Microparra capensis ) adalah burung perandai dalam keluarga Jacanidae dan dapat ditemukan di Afrika. Ia dijumpai di habitat lahan basah di Angola, Botswana, Burkina Faso, Burundi, Kamerun, Republik Afrika Tengah, Chad, Republik Demokratik Kongo,...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Bellan RoosRoos pada 1927Lahir(1901-05-25)25 Mei 1901Nynäshamn, SwediaMeninggal8 April 1990(1990-04-08) (umur 88)Stockholm, SwediaPekerjaanPemeranTahun aktif1933-1979 Bellan Roos (25 Mei 1901 – 8 April 1990) adalah seorang p...

Gue Kapok Jatuh CintaSutradaraThomas NawilisAwi SuryadiProduser GS Marina Hanny Yanuryanty Johnson C Aoura Lovenson Chandra Ditulis olehAwi SuryadiPemeranOka AntaraDude HarlinoTeuku WisnuStan LeeBig DickyHilyani HidrantoSinematograferYunus PasolangPenyuntingDanny BayuDistributor27ant and Simple PicturesTanggal rilis 16 Februari 2006 (16 Februari 2006) Durasi110 menitNegaraIndonesia Gue Kapok Jatuh Cinta adalah sebuah film komedi romantika Indonesia yang diproduksi pada 16 Pebruari 2006. ...

تاريخ الأردنمعلومات عامةالمنطقة الأردن التأثيراتأحد جوانب الأردن تعديل - تعديل مصدري - تعديل ويكي بيانات جزء من سلسلة مقالات حولتاريخ الأردن ما قبل التاريخ عين غزال الغسولية التاريخ القديم شرق الأردن في العهد القديم عمون مؤاب إدوم الفترة الكلاسيكية الأنباط المقاطعة العر...

العلاقات الأرجنتينية البنينية الأرجنتين بنين الأرجنتين بنين تعديل مصدري - تعديل العلاقات الأرجنتينية البنينية هي العلاقات الثنائية التي تجمع بين الأرجنتين وبنين.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه الم...

For the college in Bangladesh, see Cambrian School and College. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cambrian College – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this template message) Cambrian College of Applied Arts and TechnologyTypePublic College ...

A protein that is isolated from soybean Soybean pod Soy protein is a protein that is isolated from soybean. It is made from soybean meal that has been dehulled and defatted. Dehulled and defatted soybeans are processed into three kinds of high protein commercial products: soy flour, concentrates, and isolates. Soy protein isolate has been used since 1959 in foods for its functional properties. Soy protein is generally regarded as being concentrated in protein bodies, which are estimated to co...

Gamal Abdul Nasir جمال عبد الناصر Presiden Republik Arab Bersatu Ke-1Masa jabatan22 Februari 1958 – 28 September 1970PendahuluKantor didirikanPenggantiAnwar SadatPresiden Mesir ke-2Masa jabatan23 Juni 1956 – 28 September 1970PendahuluMuhammad NaguibPenggantiAnwar SadatPerdana Menteri MesirMasa jabatan19 Juni 1967 – 28 September 1970PendahuluMuhammad Sedki SulaymanPenggantiMahmoud FawziMasa jabatan18 April 1954 – 29 September 1962Pendahu...

Balai Agung Rakyat. Istana Kebudayaan Nasional. Sepuluh Bangunan Besar (Hanzi: 十大建筑) adalah sepuluh bangunan publik yang dibangun di Beijing pada 1959 dalam rangka memperingati sepuluh tahun berdirinya Republik Rakyat Tiongkok dan sebagai inisiatif arsitektur dari program Lompatan Besar ke Depan Ketua Mao. Sebagian besar bangunan ini rampung dalam waktu sepuluh bulan karena akan diresmikan 1 Oktober 1959.[1] Selain pembangunan gedung-gedung ini, ada juga perluasan Lapangan...

كهف كاستانيامعلومات عامةالمكان Monemvasia Municipality (en) البلد اليونان الإحداثيات 36°32′45″N 23°07′28″E / 36.54584°N 23.12454°E / 36.54584; 23.12454 موقع الويب kastaniacave.gr… (الإنجليزية) تعديل - تعديل مصدري - تعديل ويكي بيانات يقع كهف كاستانيا في منطقة فويز، محافظة لاكونيا، اليونان. على بٌعد 1...
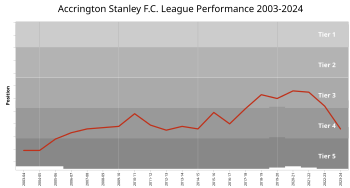
Association football club in England This article is about the current club. For the predecessor dissolved in 1962, see Accrington Stanley F.C. (1891). Not to be confused with Accrington F.C.. ASFC redirects here. For the agency abbreviated as AFSC in French, see Canada Border Services Agency. Football clubAccrington StanleyFull nameAccrington Stanley Football ClubNickname(s)The 'Owd RedsFoundedOctober 1968; 55 years ago (1968-10)GroundCrown GroundCapacity5,450 (3,100 s...

Vowel sound represented by ⟨ʉ⟩ in IPA Close central rounded vowelʉIPA Number318Audio sample source · helpEncodingEntity (decimal)ʉUnicode (hex)U+0289X-SAMPA}Braille Image IPA: Vowels Front Central Back Close i y ɨ ʉ ɯ u Near-close ɪ ʏ ʊ Close-mid e ø ɘ ɵ ɤ o Mid e̞ ø̞ ə ɤ̞ o̞ Open-mid ɛ œ ɜ ɞ ʌ ɔ Near-open æ ɐ Open a ɶ ä ɑ ɒ IPA help audio full chart template Legend: unrounded • rounded A spectrogram of /ʉ/. The ...

French fighter pilot Jacques Louis AndréJacques André in May 1946.Born(1919-02-25)25 February 1919Paris, FranceDied2 April 1988(1988-04-02) (aged 69)Antibes, FranceAllegiance FranceService/branchFrench Air ForceYears of service1939 – 1968RankColonelUnitNormandie-Niemen RegimentAwardsHero of the Soviet UnionLegion of Honour Jacques André (25 February 1919 – 2 April 1988) was a French fighter pilot in the Normandie-Niemen Regiment, which flew on the Eastern Front o...

Richard O'BrienO'Brien pada tahun 2006LahirRichard Timothy Smith25 Maret 1942 (umur 82)[1]Cheltenham, Gloucestershire, England, UKPekerjaanAktor, pengarang, penyiar, aktor suara, pemain teaterPeriode1965–sekarangGenreCult filmKarya terkenalThe Rocky Horror Show (penulis and aktor)The Crystal Maze (pembawa acara)PasanganKimi Wong (m. 1971–?, cerai)Jane Moss (m. 1983–2006, cerai)Anak3Websitehttp://www.rockyhorror.com Richard Timothy Smith (lahir 25 Maret 1942), yang lebi...

عملية كارني شومرون موقع العملية المعلومات البلد إسرائيل الموقع كارني شومرون، الضفة الغربية الإحداثيات 32°10′29.46″N 35°05′27.86″E / 32.1748500°N 35.0910722°E / 32.1748500; 35.0910722 التاريخ 16 فبراير 20027:45 مساء (ت.غ+2) نوع الهجوم عملية انتحارية الخسائر الوفيات 3 (+ المنفذ) الإصابات 27 (ستة...

Benaguacil Benaguasil municipio de España y municipio de la Comunidad Valenciana Escudo Vista de la localidad BenaguacilUbicación de Benaguacil en España BenaguacilUbicación de Benaguacil en la provincia de ValenciaPaís España• Com. autónoma Comunidad Valenciana• Provincia Valencia• Comarca Campo de Turia• Partido judicial Llíria[1]Ubicación 39°35′36″N 0°35′11″O / 39.593333333333, -0.58...

Latin phrase meaning dare to know Sapere aude is the Latin phrase meaning Dare to know; and also is loosely translated as Have courage to use your own reason, Dare to know things through reason. Originally used in the First Book of Letters (20 BC), by the Roman poet Horace, the phrase Sapere aude became associated with the Age of Enlightenment, during the 17th and 18th centuries, after Immanuel Kant used it in the essay Answering the Question: What Is Enlightenment? (1784). As a philosopher, ...

For related races, see 2022 United States treasurer elections. 2022 Oklahoma State Treasurer election ← 2018 November 8, 2022 2026 → Nominee Todd Russ Charles de Coune Party Republican Democratic Popular vote 738,545 349,876 Percentage 64.77% 30.68% County results Precinct resultsRuss: 40–50% 50–60% 60–70% 70–80% &...

Roman Catholic diocese in Italy Diocese of ParmaDioecesis ParmensisParma CathedralLocationCountryItalyEcclesiastical provinceModena-NonantolaStatisticsArea2,100 km2 (810 sq mi)Population- Total- Catholics(as of 2016)339,547278,429 (82.0%)Parishes309InformationDenominationCatholic ChurchRiteRoman RiteEstablished4th centuryCathedralBasilica Cattedrale della Assunzione di Maria VirgineSecular priests151 diocesan104 (Religious Orders)24 Permanent DeaconsCurrent leade...
![{\displaystyle \forall A{\Big [}(\exists w(w\in A)\land \exists z\,\forall w(w\in A\rightarrow w\leq z))\rightarrow \exists x\,\forall y([\forall w(w\in A\rightarrow w\leq y)]\leftrightarrow x\leq y){\Big ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93af7731aa79ba0d63f0a10fd16dd33f1b6eb376)