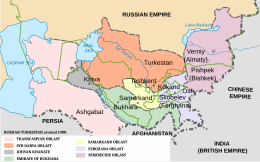
Oblast' di Fergana
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Robin DavisLahir29 Maret 1943 (umur 80)Marseille, PrancisPekerjaanSutradara, penulis naskahTahun aktif1975-2006 Robin Davis (lahir 29 Maret 1943) adalah seorang sutradara dan penulis naskah asal Prancis. Ia menyutradarai 13 film antara 1975 ...

Dewan Perwakilan Rakyat Daerah Kota Sungai PenuhDewan Perwakilan RakyatKota Sungai Penuh2019-2024JenisJenisUnikameral SejarahSesi baru dimulai28 Agustus 2019PimpinanKetuaH. Fajran, S.P., M.Si. (Demokrat) sejak 21 Oktober 2019 Wakil Ketua ISatmar Lendan, DPT (PAN) sejak 21 Oktober 2019 Wakil Ketua IISyafriadi, S.H. (Hanura) sejak 21 Oktober 2019 KomposisiAnggota25Partai & kursi PDI-P (1) NasDem (2) PKB (1) Hanura (3) De...

لمعانٍ أخرى، طالع محمد عبد الرحمن (توضيح). هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يناير 2018) محمد عبد الرحمن معلومات شخصية الطول 175 سنتيمتر الجنسية بحريني الحياة العملية المهنة رياضي الرياضة الر...

Jaringan tulang sejati sebagai contoh jaringan ikat Jaringan ikat adalah jaringan yang memiliki fungsi untuk mengikat serta menyokong bagian jaringan yang lain.[1] Penyusun jaringan ikat adalah sel yang tersusun dalam suatu matriks ekstraseluler dan tersusun menyebar.[1] Matrik tersebut biasanya berupa cairan, benda kenyal seperti agar dan padatan.[1] Jaringan ikat ada beberapa macam yaitu jaringan ikat longgar, jaringan adiposa, jaringan ikat berserat, tulang rawan, t...

Saison 2019-2020 de l'Olympique lyonnais Généralités Couleurs Rouge, bleu et blanc Stade Parc Olympique lyonnais59 186 places Président Jean-Michel Aulas Entraîneur Sylvinho(jusqu'au 7 octobre 2019) puis Rudi Garcia (à partir du 14 octobre 2019) Résultats Championnat 7e 40 points (11V, 7N, 10D)(42 buts pour, 26 contres) Coupe de France Éliminé en 1/2 finale par le Paris Saint Germain Coupe de la Ligue Finaliste contre Paris Saint Germain Ligue des Champions Éliminé e...

Bureau-bibliothèque di Pierre Chareau, Musée des Arts Décoratifs, Paris Pierre Chareau (Bordeaux, 4 agosto 1883 – New York, 24 agosto 1950) è stato un architetto e designer francese, autore della celebre Casa di vetro. Indice 1 Biografia 2 Opere realizzate 3 Bibliografia 4 Altri progetti 5 Collegamenti esterni Biografia Studiò all'Ecole des Beaux-Arts a Parigi dal 1900 al 1908. Prima di mettersi in proprio nel 1919, aveva lavorato nella sede parigina della ditta inglese Waring and Gill...

American newspaper editor and politician Moses Sperry Beach portrait, picture from the book The Innocents Abroad Moses Sperry Beach (October 5, 1822 – July 25, 1892) was an American newspaper owner, editor, inventor, and politician from New York. His papers were the Boston Daily Times and the New York Sun. He ran the Sun through most of the American Civil War, and was active during the presidency of Abraham Lincoln. He was featured in Mark Twain's book The Innocents Abroad, after embarking ...

List of Canadian events in 2007 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2007 in Canada – news · newspapers · books · scholar · JSTOR (September 2023) (Learn how and when to remove this message) ← 2006 2005 2004 2007 in Canada → 2008 2009 2010 Decades: 1980s 1990s 2000s 2010s 2020s See als...

Resolusi 993Dewan Keamanan PBBWilayah Gali (ditandai)Tanggal12 Mei 1995Sidang no.3.535KodeS/RES/993 (Dokumen)TopikAbkhazia, GeorgiaRingkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDitandaiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Rusia Britania Raya Amerika SerikatAnggota tidak tetap Argentina Botswana Republik Ceko Jerman Honduras Indonesia Italia Nigeria Oman Rwanda Resolusi ...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Town and municipality in Puerto Rico City and municipality in Puerto Rico, United StatesRío Grande Municipio de Río GrandeCity and municipalityTrees in Mameyes II, Río Grande FlagCoat of armsNickname: La Ciudad de El YunqueAnthem: Entre las ondas que jugueteanMap of Puerto Rico highlighting Río Grande MunicipalityCoordinates: 18°22′49″N 65°49′53″W / 18.38028°N 65.83139°W / 18.38028; -65.83139Sovereign state United StatesCommonwealth Puert...

Railway line in Fukuoka Prefecture, Japan Itoda LineA Heisei Chikuhō 400-series train on the Itoda Line at Buzen-Ōkuma StationOverviewNative name糸田線Owner Heisei Chikuhō RailwayLocaleFukuoka PrefectureTerminiKanadaTagawa-GotōjiStations6Websitewww.heichiku.netServiceTypeHeavy railHistoryOpened20 October 1897 (1897-10-20)TechnicalLine length6.8 km (4.2 mi)Track gauge1,067 mm (3 ft 6 in)ElectrificationNone Route map The Itoda Line (糸田線,...

Protest events in Xinjiang, China July 2009 Ürümqi riotsPart of the Xinjiang conflictRioters besieging a bus in Tianshan, Ürümqi, attacking escaping Han passengers with sticks.Date5–8 July 2009LocationÜrümqi, Xinjiang, ChinaCaused byAnger over the Shaoguan incidentParties UyghursSupported by:World Uyghur Congress (alleged; denied) Han and Hui Government of China Ministry of Public Security People's Police People's Armed Police Lead figures Wang Lequan Nur Bekri Number 3,000+[1]...

Vector graphics editor from Adobe Inc. Adobe IllustratorDeveloper(s)AdobeInitial releaseMarch 19, 1987; 37 years ago (1987-03-19)Stable release28.6 / July 23, 2024; 4 days ago (2024-07-23) Written inC++, ActionScriptOperating system Windows 10 (64-bit) v22H2 or later macOS 11.0 or later iPadOS 14 or later TypeVector graphics editorLicenseProprietaryWebsiteadobe.com/illustrator Adobe Illustrator is a vector graphics editor and design software developed and m...

Tierra Caliente Localización geográficaContinente AméricaRegión NorteaméricaLocalización administrativaPaís México MéxicoEstados Colima Estado de México Guerrero Jalisco Michoacán Estado de MorelosCaracterísticas geográficasTipo DepresiónValleCuerpos de agua Río AmacuzacRío BalsasRío CupatitzioRío TepalcatepecCiudades Cuernavaca Cuautla Colima Iguala Apatzingán Nueva Italia Tejupilco Arcelia Ciudad Altamirano HuetamoClima Templado subhúmedoSecoMapas ...

French historian (born 1934) Serge BersteinBorn1934Academic workMain interestsFrench Third Republic Serge Berstein (born in 1934) is a French historian, well known as a specialist of the French Third Republic. He is a reader at Institut d'Études Politiques de Paris.[1] References ^ Berstein - Centre d'histoire de Sciences Po. sciences-po.fr. Authority control databases InternationalISNIVIAFFASTWorldCatNationalGermanyUnited StatesFranceBnF dataItalyAustraliaCzech RepublicSpainPortugal...

1956 single by Bill Buchanan and GoodmanThe Flying SaucerSingle by Bill Buchanan and GoodmanReleasedJuly 1956Genre Mashup novelty break-in sound collage[1][2] Length4:17 (both parts)Label Luniverse Songwriter(s) Bill Buchanan Dickie Goodman Bill Buchanan and Goodman singles chronology The Flying Saucer (1956) Buchanan and Goodman on Trial (1956) The Flying Saucer (also known as The Flying Saucer Parts 1 & 2) is a novelty record, the first of a series of break-in records re...

Flying Microtonal Banana Студийный альбом King Gizzard & The Lizard Wizard Дата выпуска 24 февраля 2017 Жанр психоделический рок Длительность 41:53 Страна Австралия Язык песен английский Лейблы Flightless Heavenly ATO Хронология King Gizzard & The Lizard Wizard Nonagon Infinity(2016) Flying Microtonal Banana(2017) Murder of the Universe(2017) Flying Microton...

Chemical engineering technique The McCabe–Thiele method is a technique that is commonly employed in the field of chemical engineering to model the separation of two substances by a distillation column.[1][2][3] It uses the fact that the composition at each theoretical tray is completely determined by the mole fraction of one of the two components. This method is based on the assumptions that the distillation column is isobaric—i.e the pressure remains constant—an...

In matematica, un gruppo quoziente è una particolare struttura algebrica che è possibile costruire a partire da un dato gruppo e un suo sottogruppo normale. Indice 1 Definizione 1.1 Premessa 1.2 Gruppo quoziente 2 Struttura di gruppo 3 Proiezione 4 Note 5 Bibliografia 6 Voci correlate Definizione Premessa Sia G {\displaystyle G} un gruppo, e H {\displaystyle H} un suo sottogruppo normale. Si può introdurre la relazione di equivalenza su G {\displaystyle G} definita, per ogni g , g ′...