Bernard Bolzano
|
Read other articles:

Veolia Environnement S.A.JenisSociété AnonymeKode emitenEuronext: VIELSE: 0NY8CAC 40 ComponentISINFR0000124141IndustriJasa lingkungan hidupDidirikan1853; 170 tahun lalu (1853) (Compagnie Générale des Eaux)1998; 26 tahun lalu (1998) (Vivendi)2003; 21 tahun lalu (2003) (Veolia Environnement)KantorpusatParis, PrancisTokohkunciAntoine Frérot (Chairman dan CEO)JasaPenjernihan air, pengelolaan sampah, HVAC, lampu jalan, layanan manajemen fasilitasPendapatan€24.390 miliar ...

Pronunciation change in English between 1350 and 1700 History and description ofEnglish pronunciation Historical stages Old English Middle English General development In Old English In Scots Development of vowels A Close back Close front Diphthongs Great Vowel Shift Open back Pre-L Pre-R Development of consonants Single consonants Clusters Variable features Cot–caught merger Drawl Flapping H-dropping L-vocalization NG R Rhoticity T-glottalization TH WH Related topics History of English Spel...

Boxing competitions Boxing at the African GamesBoxingFirst event1965 BrazzavilleOccur everyfour yearsLast event2011 MaputoNext event2015 RabatBest Algeria (ALG) Boxing was an African Games event at its inaugural edition in 1965 and has continued to feature prominently at the competition in each of its subsequent editions. Editions Games Year Host city Best nation I 1965 Brazzaville Egypt II 1973 Lagos Nigeria III 1978 Algiers Kenya IV 1987 Nairobi Kenya V 199...

Prime Minister of Papua New Guinea The HonourableJames MarapeMPMarape in 20239th Prime Minister of Papua New GuineaIncumbentAssumed office 30 May 2019MonarchsElizabeth IICharles IIIGovernor‑GeneralSir Bob DadaeDeputyDavis Steven (2019–2020)Sam Basil (2020–2022)John Rosso (2022–present)Preceded byPeter O'NeillMinister of Foreign AffairsIncumbentAssumed office 12 May 2023[1]Prime MinisterHimselfPreceded byJustin TkatchenkoMinister of FinanceIn officeAugust 2012&...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Jürgen Melzer – berita · surat kabar · buku · cendekiawan · JSTOR Jürgen MelzerKebangsaan AustriaTempat tinggalDeutsch-Wagram, AustriaTinggi182 m (597 ft 1+1⁄2 in)Berat75 ...

Football league seasonCopa PerúSeason1970ChampionsAtlético TorinoMatches played15Goals scored35 (2.33 per match)Top goalscorerFernando Guerrero (4)Highest scoringDefensor Casagrande 6–3 Garcilaso Only National Stage taken into consideration← 1969 1971 → The 1970 Copa Perú season (Spanish: Copa Perú 1970), the promotion tournament of Peruvian football. In this tournament after many qualification rounds, each one of the 24 departments in which Peru is politically divided, qualify...

Knight's Cross recipientsAllgradesGrand CrossGolden Oak Leaves, Swordsand DiamondsOak Leaves, Swords and DiamondsOak Leaves and SwordsOakLeaves 1940–41 1942 1943 1944 1945 Foreign Knight'sCross A Ba–Bm Bn–Bz C D E F G Ha–Hm Hn–Hz I J Ka–Km Kn–Kz L M N O P Q R Sa–Schr Schu–Sz T U V W X–Z Foreign Knight's Cross The Knight's Cross of the Iron Cross (German: Ritterkreuz des Eisernen Kreuzes) and its variants were the highest awards in the military and paramilitary force...

Three person research deep-submergence vehicles History United States NamePisces IV and Pisces V OwnerNational Oceanic and Atmospheric Administration OperatorHawaii Undersea Research Laboratory BuilderHyco International Hydrodynamics, North Vancouver CompletedEarly 1970s General characteristics Displacement13,000kg Length6.10 m (20 ft 0 in) Beam3.20 m (10 ft 6 in) Height3.35 m (11 ft 0 in) Propulsion2 × side-mounted reversible thrusters tiltable t...

Sir Alexander FlemingSir Alexander FlemingLahir(1881-08-06)6 Agustus 1881Lochfield, Ayrshire, SkotlandiaMeninggal11 Maret 1955(1955-03-11) (umur 73)London, InggrisKebangsaanSkotlandiaWarga negaraInggrisAlmamaterInstitusi Politeknik RoyalSekolah Kedokteran Rumah Sakit St MaryPerguruan Tinggi Imperial LondonDikenal atasPenemuan penisilinPenghargaan FRS (1943)[1] Penghargaan Nobel Fisiologi atau Kedokteran (1945)[2] FRSE FRCS(Eng) Knight Bachelor (1944) Karier ilmiahBidangB...
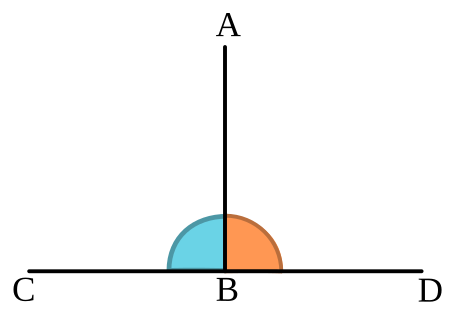
90° angle (π/2 radians) For other uses, see Right angle (disambiguation). A right angle is equal to 90 degrees. A line segment (AB) drawn so that it forms right angles with a line (CD) Types of angles 2D angles Right Interior Exterior Spherical 2D angle pairs Adjacent Vertical Complementary Supplementary Transversal 3D angles Dihedral Solid vte In geometry and trigonometry, a right angle is an angle of exactly 90 degrees or π {\displaystyle \pi } /2 radians[1] corresponding t...

Sport in Canada For other rugby, see Rugby in Canada. Rugby league in CanadaThe Toronto Wolfpack take the field against the London Broncos during the Challenge CupCountryCanadaGoverning bodyCanada Rugby LeagueNational team(s) Men's national team Women's national team First played1928National competitions Rugby League World Cup Rugby league football (French: Rugby à XIII) is a participation and spectator sport in Canada. History Games related to rugby football have been played in Canada since...

Pagoda Doi Inthaon Doi Inthanon merupakan tempat tertinggi di Thailand yang memiliki ketinggian sekitar 2.565 – 3341 meter di atas laut. Berlokasi di Chiang Mai di bagian Utara Thailand. Doi Inthanon merupakan taman nasional terpopuler di Negeri Gajah Putih. Taman ini luasnya 482 kilometer persegi. Doi Inthanon merupakan taman nasional yang memiliki banyak tempat cantik dan bersejarah, antara lain Royal Agricultural Station,Ban Mae Klang Luang, dan Wachirathan Waterfall.Doi Inthanon merupak...

American screenwriter (1900–1995) Albert HackettHackett with his wife Frances GoodrichBornAlbert Maurice Hackett(1900-02-16)February 16, 1900Nutley, New Jersey, U.S.DiedMarch 16, 1995(1995-03-16) (aged 95)New York City, U.S.OccupationDramatistscreenwriteractorSpouse Frances Goodrich (m. 1931; died 1984) Gisella Svetlik (m. 1985) ParentsFlorence Hackett (mother)Arthur V. Johnson (stepfather)Relati...

Indian actress AnumolBornNaduvattam, Tamil Nadu, IndiaOccupationsActressBharathanatiyam dancerYears active2010–present Anumol is an Indian actress, predominantly acting in Malayalam and Tamil films.[1] She appeared in Malayalam films such as Chayilyam (2014), Ivan Megharoopan (2012), Akam (2011), Vedivazhipadu (2013) and Jamna Pyari (2015).Her performance as Kuruvammal in 2023 Tamil web-series Ayali applauded by Critics and Audience.[2][3][4][5]&...

この項目では、映画作品について説明しています。INFINITY16 welcomez MINMI,10-FEETの曲については「真夏のオリオン (INFINITY16の曲)」をご覧ください。 真夏のオリオン Last Operations Under the Orion監督 篠原哲雄脚本 長谷川康夫飯田健三郎原作 池上司製作総指揮 市川南佐倉寛二郎出演者 玉木宏北川景子堂珍嘉邦平岡祐太黄川田将也吉田栄作吹越満益岡徹音楽 岩代太郎撮影 山本英�...

Der Bayerische Kabarettpreis ist eine Auszeichnung für Satiriker in Deutschland, die seit 1999 jährlich vergeben wird. Inhaltsverzeichnis 1 Allgemeines 2 Preisträger 3 Einzelnachweise 4 Weblinks Allgemeines Bayerischer Kabarettpreis 2003, an Hans Liberg, Vince Ebert, Urban Priol (von links nach rechts) Sissi Perlinger, Preisträgerin 2008 Annamateur, Preisträgerin 2010 Max Uthoff, Senkrechtstarter-Preis 2013 Luise Kinseher, Preisträgerin 2014 Carolin Kebekus, Preisträgerin 2022 Till Rei...

1982 exegesis by Saul Kripke Wittgenstein on Rules and Private Language AuthorSaul A. KripkeLanguageEnglishSubjectsPhilosophy of languagePublisherHarvard University PressPublication date1982Publication placeUnited StatesPages150ISBN0-674-95401-7 Part of a series onLudwig Wittgenstein Early philosophy Picture theory of language Truth tables Truth conditions Truth functions State of affairs Logical necessity Later philosophy Meaning as use Language-game Private language argument Family resembla...

Contea di KinneyconteaContea di Kinney – VedutaTribunale della contea LocalizzazioneStato Stati Uniti Stato federato Texas AmministrazioneCapoluogoBrackettville Data di istituzione1850 TerritorioCoordinatedel capoluogo29°21′00″N 100°25′12″W29°21′00″N, 100°25′12″W (Contea di Kinney) Superficie3 536 km² Abitanti3 598 (2010) Densità1,02 ab./km² Altre informazioniLingueinglese Fuso orarioUTC-6 CartografiaBrackettville Contea di Kinney – Mappa S...

District in North Rhine-Westphalia, GermanyHöxterDistrict FlagCoat of armsCountryGermanyStateNorth Rhine-WestphaliaAdm. regionDetmoldCapitalHöxterGovernment • District admin.Michael Stickeln (CDU)Area • Total1,201.42 km2 (463.87 sq mi)Population (31 December 2023)[1] • Total141,883 • Density120/km2 (310/sq mi)Time zoneUTC+01:00 (CET) • Summer (DST)UTC+02:00 (CEST)Vehicle registrationHX, WARWebsiteht...

Railway station in Berlin, Germany For the street, see Frankfurter Allee. For the Berlin U-Bahn station, see Frankfurter Allee (Berlin U-Bahn). Frankfurter Allee Through stationEntrance buildingGeneral informationLocationBerlin, BerlinGermanyCoordinates52°30′51″N 13°28′29″E / 52.51417°N 13.47472°E / 52.51417; 13.47472Owned byDB NetzOperated byDB Station&ServiceLine(s)Ringbahn (KBS 200.41, 200.42, 200.8, 200.85)Platforms1 island platformTracks2Connection...
