מונה אי נשיג
|
Read other articles:

San Gregorio nelle AlpiKomuneComune di San Gregorio nelle AlpiNegara ItaliaWilayahVenetoProvinsiBelluno (BL)FrazioniVelos, Muiach, Roncoi, Donce, Paderno, Alconis, Tassin, Gasnil, Cargnach, Paluch, Cort, Saltoi, Barp, Caval, Paluch, Fumach, Carazzai, MaserollePemerintahan • Wali kotaErmes VieceliLuas • Total18,9 km2 (73 sq mi)Ketinggian526 m (1,726 ft)Populasi (2006) • Total1.578 • Kepadatan8,3/km2 (22/sq ...

Pesta Olahraga Asia Tenggara Ke-28Logo Pesta Olahraga Asia Tenggara 2015Logo Pesta Olahraga Asia Tenggara 2015Tuan rumahSingapura SingapuraMotoCelebrate the Extraordinary(merayakan yang luar biasa)Jumlah negara11Jumlah atlet4370Jumlah disiplin402 dalam 36 cabang olahragaUpacara pembukaan5 Juni 2015Upacara penutupan16 Juni 2015Dibuka olehTony TanPresiden SingapuraDitutup olehTony TanPresiden SingapuraJanji atletMicky LinPenyalaan oborFandi AhmadIrfan FandiTempat utamaStadion Nasional Sing...

Jumeirah Lakes Towers —— Permukiman di Uni Emirat Arab —— Jumeirah Lakes Towersابراج بحيرة الجميرا Negara Uni Emirat Arab Emirat Dubai Kota Dubai Statistik permukiman Luas 18 kilometer persegi (6,9 sq mi) Permukiman sekitarnya Jumeirah Islands, Dubai Marina, Emirates Hills Dubai Metro station Jumeirah Lakes Towers Koordinat 25°04′32″N 55°08′43″E / 25.07557°N 55.14536°E / 25.07557; 55.14536Koord...

A request that this article title be changed to The Singing Bee is under discussion. Please do not move this article until the discussion is closed. American TV series or program The Singing BeeTitle screen.Created byPhil GurinBob HorowitzPresented byJoey FatoneMelissa PetermanStarringSteve Dorff and the Bee Hive, CMT Ray Chew and the Groove, NBC The Honey Bees, NBCCountry of originUnited StatesOriginal languageEnglishNo. of seasons5No. of episodes66 (total)ProductionExecutive producersP...

Lizzie VelasquezVelásquez pada Festival Buku Texas 2017LahirElizabeth Ann Velásquez13 Maret 1989 (umur 35)Austin, Texas, Amerika SerikatKebangsaanAmerika SerikatNama lainLizzie VelásquezAlmamaterUniversitas Negeri TexasPekerjaanmotivator dan penulisDikenal ataspidato motivasi, aktivis antiperundungan, penampilan di publik dan pengarang bukuOrang tuaRita Borja Velásquez Guadalupe Fonsi Velásquez Elizabeth Anne Velásquez (/ˈlɪzi vəˈlæskɛz/; lahir pada 13 Maret 1989) adala...

Stasiun Matraman C14 Pintu masuk Stasiun MatramanLokasiJalan Matraman RayaKebon Manggis, Matraman, Jakarta Timur, DKI Jakarta 13150IndonesiaKoordinat6°12′45.227″S 106°51′35.370″E / 6.21256306°S 106.85982500°E / -6.21256306; 106.85982500Koordinat: 6°12′45.227″S 106°51′35.370″E / 6.21256306°S 106.85982500°E / -6.21256306; 106.85982500Operator KAI Commuter Letakkm 1+285 lintas Manggarai–Matraman–Jatinegara[1][...
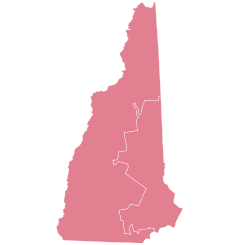
2002 United States House of Representatives elections in New Hampshire ← 2000 November 5, 2002 2004 → All 2 New Hampshire seats to the United States House of Representatives Majority party Minority party Party Republican Democratic Last election 2 0 Seats won 2 0 Seat change Popular vote 254,797 175,905 Percentage 57.46% 39.67% Swing 2.93% 3.27% Republican 50–60% Elections in New Hampshire Federal government Presiden...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

1995 studio album by Candi StatonIt's Time!Studio album by Candi StatonReleased1995GenreGospelLabelIntersound[1]ProducerMarcus WilliamsCandi Staton chronology I Give You Praise(1993) It's Time!(1995) Cover Me(1997) It's Time! is an album by the American singer Candi Staton.[2][3] It was released in 1995.[4] The album was nominated for a National Association of Independent Recording Distributors and Manufacturers Award, in the Gospel/religious category.&...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Questa voce sugli argomenti California e stazioni e comprensori sciistici è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. La pista Gunbarrel innevata Heavenly Valley, o Heavenly Mountain Resort, è un comprensorio sciistico statunitense che si estende nella Sierra Nevada tra la California e il Nevada, costeggiando a sud il Lago Tahoe. Attrezzato con 97 piste e 30 impianti di risalita, si estende per 19 km². Centro amministrativo del comprensorio...

American anthropologist (1933–2009) Melvin EmberMel Ember, ca. 1990BornJanuary 13, 1933Brooklyn, NYDiedSeptember 27, 2009 (aged 76)New Haven, CTCitizenshipAmericanAlma materYale UniversityKnown forcross-cultural research kinship studies scientific anthropologyAwardsFellow, American Association for the Advancement of ScienceScientific careerFieldsanthropology, ethnology, cross-cultural studiesInstitutionsCity University of New York, Human Relations Area FilesAcademic advisorsGeorge...

Maritime patrol and anti-submarine aircraft family P-3 Orion A P-3C of the Japan Maritime Self-Defense Force Role Maritime patrol aircraftType of aircraft National origin United States Manufacturer Lockheed Lockheed Martin Kawasaki Aerospace Company First flight November 1959[1] Introduction August 1962[1] Status Active Primary users United States NavyRepublic of China Navy Japan Maritime Self-Defense Force Republic of Korea Navy Produced 1961–1990[2] Number bui...

Secret post-WWII United States program Project Paperclip redirects here. For the Holocaust project, see Paper Clips Project. For other uses, see Paper clip (disambiguation). Not to be confused with Operation Paper, a 1951–52 CIA operation. Kurt H. Debus, a former V-2 rocket scientist who became a NASA director, sitting between U.S. President John F. Kennedy and U.S. Vice President Lyndon B. Johnson in 1962 at a briefing at Blockhouse 34, Cape Canaveral Missile Test Annex Operation Paperclip...

Men's long jumpat the Games of the XXIX OlympiadIrving Saladino (2007 world championships)VenueBeijing Olympic StadiumDates16 August 2008 (qualifying)18 August 2008 (final)Competitors38 from 32 nationsWinning distance8.34Medalists Irving Saladino Panama Khotso Mokoena South Africa Ibrahim Camejo Cuba← 20042012 → Athletics at the2008 Summer OlympicsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen5000 mmenwomen10,000 m...

Disambiguazione – Se stai cercando altri significati, vedi Senato (disambigua). Palazzo Madama, sede del Senato della Repubblica, a Roma Senato è il nome che, nel parlamento della maggior parte degli ordinamenti bicamerali, è attribuito a una delle due camere e, precisamente, alla cosiddetta camera alta. Indice 1 Etimologia 2 Il senato come camera alta 3 Ruolo nell'equilibrio dei poteri 4 Altri significati 5 Nella cultura di massa 6 Note 7 Bibliografia 8 Altri progetti 9 Collegamenti est...

Universitas LeipzigUniversität Leipzigbahasa Latin: Alma mater Lipsiensis Tampilkan peta yang diperbesarTampilkan peta yang diperkecil InformasiMotoAus Tradition Grenzen überschreitenMoto dalam bahasa InggrisCrossing Boundaries out of TraditionJenispublikDidirikan2 December 1409RektorBeate SchückingStaf administrasi3.246 (2010)[1]Jumlah mahasiswa28.125 (musim dingin 2011/12)[1]LokasiLeipzig, Saxony, JermanKampusUrbanSitus webuni-leipzig.de Universitas...

Railway station in West Bengal, India Maliya Kolkata Suburban Railway stationGeneral informationLocationMaliya, Hooghly district, West BengalIndiaCoordinates22°49′54″N 88°08′09″E / 22.831567°N 88.135964°E / 22.831567; 88.135964Elevation13 metres (43 ft)Owned byIndian RailwaysOperated byEastern RailwayLine(s)Sheoraphuli–Tarakeswar branch linePlatforms2Tracks2ConstructionStructure typeStandard (on-ground station)Bicycle facilitiesYesOther informationSt...

Pour les articles homonymes, voir Dassault. 8e arrtRond-point des Champs-Élysées-Marcel-Dassault Vue du côté nord. Situation Arrondissement 8e Quartier Champs-ÉlyséesFaubourg-du-Roule Historique Création 1670 Dénomination Arrêté municipal du 9 décembre 1991 Ancien nom Rond-point des Champs-Élysées Géocodification Ville de Paris 1739 DGI 1735 Géolocalisation sur la carte : Paris Rond-point des Champs-Élysées-Marcel-Dassault Géolocalisation sur la carte : 8e ar...
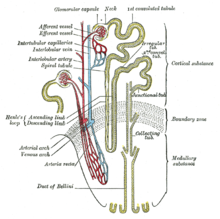
Medical conditionBartter syndromeOther namesSalt-wasting nephropathy[1]Scheme of renal tubule and its vascular supply.SpecialtyEndocrinology Bartter syndrome (BS) is a rare inherited disease characterised by a defect in the thick ascending limb of the loop of Henle, which results in low potassium levels (hypokalemia),[2] increased blood pH (alkalosis), and normal to low blood pressure. There are two types of Bartter syndrome: neonatal and classic. A closely associated di...












