Xeometría non euclidiana
|
Read other articles:
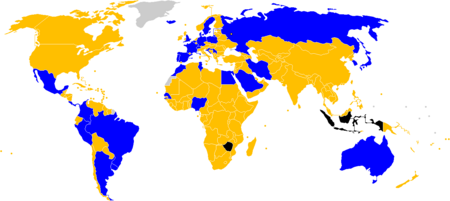
Selecciones clasificadas para el Mundial de 2018 Selecciones que no se clasificaron Equipos suspendidos Países que no son miembros de la FIFA La XXI Copa Mundial de Fútbol se celebró en Rusia entre el 14 de junio y el 15 de julio de 2018. Para su fase final se clasificaron 32 selecciones. Dichas selecciones fueron divididas en 8 grupos de cuatro, para posteriormente prose...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

2008 studio album by Killer Mike I Pledge Allegiance to the Grind IIStudio album by Killer MikeReleasedJuly 8, 2008RecordedOctober 2007 – January 2008GenreHip hopLength1:15:31LabelGrind Time OfficialSMC Recordings FontanaProducerYoung SearsCKP ProductionsWonder AilloTha BiznessCutmaster SwiffThe CancerKidz With Machine GunzNo I.D.Tyrice JonesX.P.Smiff & CashB DonD.R.U.G.S. BeatsTec BeatzMalayKiller Mike chronology I Pledge Allegiance to the Grind(2006) I Pledge Allegiance to the Gri...

PemberitahuanTemplat ini mendeteksi bahwa artikel bahasa ini masih belum dinilai kualitasnya oleh ProyekWiki Bahasa dan ProyekWiki terkait dengan subjek. Perhatian: untuk penilai, halaman pembicaraan artikel ini telah diisi sehingga penilaian akan berkonflik dengan isi sebelumnya. Harap salin kode dibawah ini sebelum menilai. {{PW Bahasa|importance=|class=}} Terjadi [[false positive]]? Silakan laporkan kesalahan ini. 09.43, Minggu, 31 Maret, 2024 (UTC) • hapus singgahan Seba...

Swietenia macrophylla Status konservasiGentingIUCN32293 TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsKladcore eudicotsKladSuperrosidaeKladrosidsKladmalvidsOrdoSapindalesFamiliMeliaceaeGenusSwieteniaSpesiesSwietenia macrophylla King, 1886 Tata namaSinonim takson Swietenia belizensis Lundell Swietenia candollei Pittier Swietenia krukovii Gleason Swietenia macrophylla var. marabaensis Ledoux & Lobato Swietenia tessmannii Harms [1]Dis...

Eparki Santo Vladimir-Le-Grand de ParisEparchia Sancti Vladimiri Magni in urbe Parisiensi pro Ucrainis ritus ByzantiniDiocèse de Saint-Vladimir-le-Grand de ParisGereja Katolik Yunani Ukraina Katedral St. VladimirLokasiNegara PrancisMetropolitSubyek langsung Tahta SuciStatistikPopulasi- Katolik(per 2013)25,400Paroki16InformasiDenominasiGereja Katolik Yunani UkrainaGereja sui iurisGereja Katolik Yunani UkrainaRitusRitus BizantiumPendirian22 Juli 1960KatedralKatedral St. Vladimir...

Assassin of John F. Kennedy (1939–1963) Kennedy's assassin redirects here. For the assassin of Robert F. Kennedy, see Sirhan Sirhan. Lee Harvey OswaldOswald on November 23, 1963, one day after the assassination of U.S. president John F. KennedyBorn(1939-10-18)October 18, 1939New Orleans, Louisiana, U.S.DiedNovember 24, 1963(1963-11-24) (aged 24)Parkland Hospital, Dallas, Texas, U.S.Cause of deathGunshot woundResting placeRose Hill Cemetery, Fort Worth, Texas, U.S.32°43′57″N 9...

Defunct American collegiate fraternity For other uses, see Phi Kappa (disambiguation). Phi KappaΦΚFoundedOctober 1, 1889; 134 years ago (1889-10-01)Brown UniversityTypeSocialAffiliationNIC (former)EmphasisCatholic studentsScopeNational (US)MottoLoyalty to God and CollegeMember badgeColors Purple, White and GoldFlowerOphelia RoseJewelAmethystPublicationYippa-Yappa later, The TempleChapters40 installedMerged, to createPhi Kappa Theta (195...

American television sitcom Easy StreetGenreSitcomCreated byHugh WilsonAndy BorowitzStarringLoni AndersonJack ElamLee WeaverDana IveyJames CromwellArthur MaletOpening themeEasy Street performed by Linda JacksonComposerParmer FullerCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes22ProductionExecutive producersHugh WilsonAndy BorowitzCamera setupMulti-cameraRunning time30 minutesProduction companyViacom ProductionsOriginal releaseNetworkNBCReleaseSeptember 13,...

Questa voce o sezione sull'argomento religione non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Teofania, dal greco theophàneia, composto da theos («dio») e da phàinein («manifestarsi»), letteralmente significa «manifestazione della divinità» in forma sensibile. Altro termine usato in maniera anal...

Karl X Gustav Porträtt av Karl X Gustav som tronföljare från 1652–1653 av Sébastien Bourdon, Nationalmuseum.Han bär en marskalksstav vilket avser att framhäva hans militära bedrifter. Kung av Sverige Regeringstid 6 juni 1654–13 februari 1660(5 år och 252 dagar) Kröning 6 juni 1654 i Uppsala domkyrka Företrädare Kristina (regerande drottning av Sverige) Efterträdare Karl XI Valspråk I Gud mitt öde, han själv skall göra det (latin: In Iehovah sors mea, ipse faciet) Gemål H...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

Human settlement in EnglandMarstonSt. Nicholas' parish churchMarstonShow map of OxfordMarstonLocation within OxfordshireShow map of OxfordshireArea2.92 km2 (1.13 sq mi)Population3,398 (parish) (2011 census)[1]• Density1,164/km2 (3,010/sq mi)OS grid referenceSP5208Civil parishOld MarstonDistrictOxfordShire countyOxfordshireRegionSouth EastCountryEnglandSovereign stateUnited KingdomPost townOxfordPostcode districtOX3Dialling ...

Place in Gegharkunik, ArmeniaTsovak ԾովակA view of TsovakTsovakShow map of ArmeniaTsovakShow map of GegharkunikCoordinates: 40°10′58″N 45°38′02″E / 40.18278°N 45.63389°E / 40.18278; 45.63389CountryArmeniaProvinceGegharkunikMunicipalityVardenisElevation1,920 m (6,300 ft)Population (2011)[1] • Total2,319Time zoneUTC+4 (AMT)Postal code1612Tsovak at GEOnet Names Server Tsovak (Armenian: Ծովակ) is a village in the Var...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Political party in Bangladesh Not to be confused with Bangladesh National Awami Party-Bangladesh NAP. Bangladesh National Awami Party বাংলাদেশ ন্যাশনাল আওয়ামী পার্টিAbbreviationNAP(M)ChairpersonIvy AhmedGeneral SecretaryMuhammad Ali FaruqueFounderMuzaffar AhmedFoundedMarch 26, 1971 (1971-03-26) November 30, 1967 (1967-11-30) (as NAP (Wali)Registered09 (3 November 2008)Preceded byNAP (Wali)IdeologySoc...

Niece MotorsportsPemilikAl NieceKantor pusatStatesville, North CarolinaSeriNASCAR Seri Truk Camping WorldPembalapSeri Truk Camping World: 40. Dean Thompson (R)41. Ross Chastain, Tyler Carpenter, Justin Marks, Chad Chastain (paruh waktu)42. Carson Hocevar 44. Kris Wright45. Lawless Alan (R)SponsorSeri Truk Camping World: 40. GlobalTranz-Worldwide Express41. Eat Florida Watermelon, Worldwide Express, Aggressive STL42. Premier Security Solutions, MG Machinery, Sparco, Worldwide Express44. F.N.B....

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) العلاقات الكويتية التركية تركيا الكويت السفارات السفارة التركية في الكويت السفارة الكويتي...

Voce principale: Futbol'nyj Klub Rostov. FK RostovStagione 2015-2016Sport calcio Squadra Rostov Allenatore Gurban Berdiýew Prem'er-Liga2° Coppa di RussiaSedicesimi di finale 2014-2015 2016-2017 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti il Rostov nelle competizioni ufficiali della stagione 2015-2016. Indice 1 Stagione 2 Rosa 3 Risultati 3.1 Campionato 3.2 Coppa di Russia 4 Collegamenti esterni Stagione A sorpresa la squadra contese fino al...









