Le Mouvement Normand

Le Mouvement Normand
Tipopartido político
Ideoloxíarexionalismo
Data de fundación29 de setembro de 1969
SedeÉcaquelon
PaísFrancia
Na rede
https://www.tvnc.tv/
Twitter: MouvNorm Editar o valor en Wikidata
[ editar datos en Wikidata ]
Bandeira Normanda.
Cruz nórdica, bandeira empregada por Le Mouvement Normand.

Le Mouvement Normand (en galego: O Movemento Normando) é unha organización política francesa que avoga pola autonomía de Normandía. A diferenza de moitos grupos en Francia, rexeita o separatismo e subliña o punto de vista de que o pobo normando é unha das nacionalidades constituíntes da nación francesa.

Historia

O Mouvement Normand ten a súa orixe nos movementos franceses de extrema dereita dos anos sesenta. En 1969, a póla de Ruán da unión estudantil de ultradereita Fédération nationale des étudiants de France uniuse con l'Union pour la Région Normande en Lisieux para forma-lo Mouvement de la Jeunesse de Normandie, renomeado Mouvement Normand en 1971. Está liderado polo prominente activista de dereitas Didier Patte, que tamén é membro do Groupement de recherche et d'études sur la culture européenne (GRECE).

O Mouvement Normand ten sempre recibido os seus apoios da ultradereita francesa, especialmente da Fronte Nacional. De tódolos xeitos, en anos recentes, ten habido unha significativa captación dos membros dos partidos de centro-dereita como a Unión pola Democracia Francesa (UDF). A axenda rexionalista do Mouvement Normand recibe moita atención tódolos días na vida política normanda.

Principais obxectivos

  • Alta Normandía e Baixa Normandía deberían ser unificadas para fundar unha única rexión de Normandía.
  • O goberno rexional de Normandía debería estar provisto de máis competencias.
  • O carácter cultural único de Normandía, formado con elementos da cultura anglo-normanda así como da cultura gala, deberá ser recoñecido e preservado.

Véxase tamén

Ligazóns externas

Read other articles:

Ömer Toprak

Ömer Toprak Informasi pribadiTanggal lahir 21 Juli 1989 (umur 34)Tempat lahir Ravensburg, Jerman BaratTinggi 1,86 m (6 ft 1 in)Posisi bermain BekInformasi klubKlub saat ini Bayer 04 LeverkusenNomor 21Karier junior FV Ravensburg2005–2008 SC FreiburgKarier senior*Tahun Tim Tampil (Gol)2008–2011 SC Freiburg 68 (4)2011– Bayer 04 Leverkusen 37 (0)Tim nasional‡2008–2009 Jerman U-19 3 (1)2011– Turki 11 (2) * Penampilan dan gol di klub senior hanya dihitung dari liga...

 

List of cryptocurrencies

This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (June 2022) Market capitalizations of cryptocurrencies ( January 27, 2018) Since the creation of bitcoin in 2009, the number of new cryptocurrencies has expanded rapidly.[1] The UK's Financial Conduct Authority estimated there were over 20,000 different cryptocurrencies by the start of 2023, ...

 

Barangay Pulong Buhangin, Santa Maria, Bulacan

Barangay Pulong BuhanginBarangayRegionLuzon TengahProvinsiBulacanMunisipalitasSanta MariaPemerintahan • JenisBarangay • Kepala BarangaySimplicio HermogenesZona waktuGMT (UTC+8) • Musim panas (DST) Kode pos3022Kode area telepon44Situs web[1] Pulong Buhangin adalah salah satu dari dua puluh empat barangay pada munisipalitas Santa Maria, Bulacan, Filipina. Barangay ini berbatasan dengan Barangay Caypombo, Balasing, Partida dan Pulong Yantok. lbsSanta Maria, Bu...

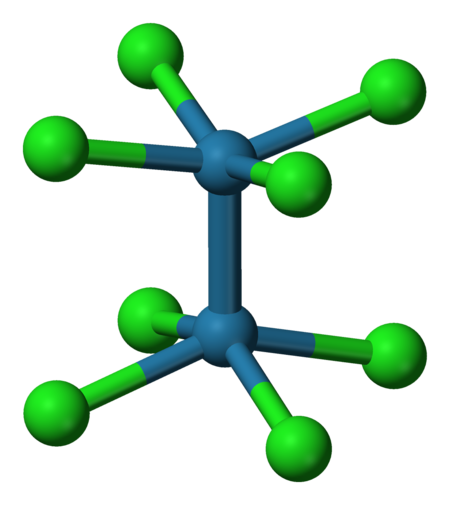
Kalium oktaklorodimolibdat

Kalium oktaklorodimolibdat(4−) Penanda Nomor CAS 25448-39-9 N 3DMet {{{3DMet}}} Nomor EC Nomor RTECS {{{value}}} CompTox Dashboard (EPA) DTXSID501045175 Sifat Rumus kimia K4Cl8Mo2 Massa molar 631.9 g/mol Penampilan kristal merah Densitas 2.54 g/cm3 Kelarutan dalam air larut Kecuali dinyatakan lain, data di atas berlaku pada suhu dan tekanan standar (25 °C [77 °F], 100 kPa). N verifikasi (apa ini YN ?) Referensi Kalium oktaklorodi...

 

Associazione Calcistica Lecce 1938-1939

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Unione Sportiva Lecce. Associazione Calcistica LecceStagione 1938-1939Sport calcio Squadra Lecce Allenatore Giovanni Battista Rebuffo Presidente G. Giorgino Serie C - Gir. H4º posto (retrocesso al 12º e ultimo posto per delibera della Presidenza Federale a caus...

 

Biara (tempat tinggal)

Biara Santa María del Parral, tempat tinggal para rahib Ordo Santo Heronimus di Segovia, Spanyol Biara Santo Nilus di Pulau Stolbnyi, di Danau Seliger dekat Ostashkov, Rusia, ca. 1910 Wihara Tengboche, biara agama Buddha di Nepal Biara Rumtek, Gangtok, Sikkim, India Biara Kerajaan di San Lorenzo de El Escorial, Spanyol. Dipangun 1563–1584. Biara Sumela, sebelah selatan Trabzon di Turki Timur. Dibangun pada abad ke-4 (diperkirakan pada 386 M). Biara adalah bangunan atau gugus bangunan yang ...

Skandal kebocoran Vatikan

Artikel ini merupakan bagian dari seriKota Vatikan Sejarah Kadipaten Roma (533–751) Donasi Pippin (750-an) Negara Kepausan (754–1870) Annatae Kongregasi untuk Perbatasan Undang-Undang Dasar Pemerintahan Sekuler Negara Gereja Penyerangan Roma oleh Muslim (846) Penaklukan Roma (1870) Tahanan dalam Vatikan (1870–1929) Permasalahan Roma Undang-Undang Jaminan Perjanjian Lateran (1929) Kota Vatikan (1929–sekarang) Gubernur Kota Vatikan Sejarah Gereja Katolik sejak 1962 Sejarah kepausan Inst...

 

Kolonisasi Bulan

Konsepsi seniman pada tahun 1986 Kolonisasi angkasa Planet Dalam Lagrange Merkurius Venus Bumi Bulan Mars Ceres Planet Luar Jupiter Europa Kalisto Saturnus Titan Uranus Objek trans-Neptunus lbs Kolonisasi Bulan adalah persiapan pendirian komunitas manusia yang permanen atau industri robot[1] di Bulan. Perencanaan Konsep seni dari NASA yang memperlihatkan astronaut sedang berada di bulan Pernyataan mengenai menempatkan sebuah koloni di Bulan telah ada sebelum Abad Luar Angkasa Perencan...

 

Рато, Родриго

Родриго Ратоисп. Rodrigo de Rato министр экономики Испании 1996 — 2000 Рождение 18 марта 1949(1949-03-18)[1][2] (75 лет)Мадрид, Испания Имя при рождении исп. Rodrigo de Rato y Figaredo Отец Рамон Рато[вд] Супруга Анхелес Аларко[вд][3] Партия Народная партия Образование Мадридский универс...

Chenouas

Berber ethnic group in northern Algeria Ethnic group ChenouisTotal population106,000Regions with significant populationsMount Chenoua, AlgeriaLanguagesChenoua and Algerian ArabicReligionSunni islam Map of Chenoui areas The Chenouis or Chenoua (Arabic: شناوة, Berber: Icenwiyen) are a Berber ethnic group native to the Chenoua Mountains in northern Algeria. They traditionally inhabit areas between the east of Ténès to the west of Cherchell. The Chenoui people number about 106,000.[cit...

 

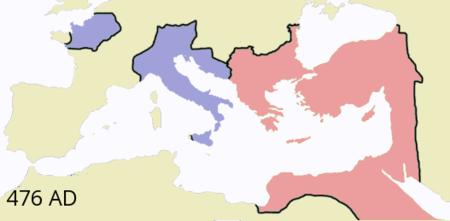
Romolo Augusto

Romolo AugustoloImperatore romano d'Occidente Nome originaleRomulus Augustus Regno31 ottobre 475 –4 settembre 476 (deposto) Nascita461 circa Mortedopo il 511 PredecessoreGiulio Nepote Successorecarica abolita(Odoacre come patrizio della diocesi d'Italia) PadreFlavio Oreste MadreFlavia Serena Flavio Romolo Augusto, noto anche con il diminutivo di Augustolo, cioè Piccolo Augusto (in latino Flavius Romulus Augustus; 461 circa – dopo il 511), è considerato tradizionalmente l'u...

 

Austin Ernst

American professional golfer Austin ErnstErnst in 2019Personal informationBorn (1992-01-31) January 31, 1992 (age 32)Greenville, South Carolina, U.S.Height5 ft 5 in (1.65 m)Sporting nationality United StatesCareerCollegeLouisiana State UniversityTurned professional2012Current tour(s)LPGA TourProfessional wins3Number of wins by tourLPGA Tour3Best results in LPGA major championshipsChevron ChampionshipT14: 2017Women's PGA C'shipT7: 2021U.S. Women's OpenT41: 2018Women's ...

Oriented strand board

Engineered wood particle board OSB is easily identifiable by its characteristic wood strands. Oriented strand board (OSB) is a type of engineered wood similar to particle board, formed by adding adhesives and then compressing layers of wood strands (flakes) in specific orientations. It was invented by Armin Elmendorf in California in 1963.[1] OSB may have a rough and variegated surface with the individual strips of around 2.5 cm × 15 cm (1.0 by 5.9 inches), lying uneve...

 

List of companies of India

Location of India India is a country in South Asia. It is the seventh-largest country by area, the second-most populous country (with over 1.4 billion people), and the most populous democracy in the world. The Indian economy is the world's fifth largest by nominal GDP and third largest by purchasing power parity.[1][2] Following market-based economic reforms in 1991, India became one of the fastest-growing major economies and is considered a newly industrialised country. For ...

 

Vorst (Brussel)

VorstForest Gemeente in België (Details) (Details) Geografie Gewest België Arrondissement Brussel-Hoofdstad Oppervlakte– Onbebouwd– Woongebied– Andere 6,29 km² (2022)3,61%30,53%65,87% Coördinaten 50° 49' NB, 4° 19' OL Bevolking (bron: Statbel) Inwoners– Mannen– Vrouwen– Bevolkings­dichtheid 58.044 (01/01/2024) 48,49% 51,51% 9224,98 inw./km² Leeftijdsopbouw– 0-17 jaar– 18-64 jaar– 65 jaar en ouder (01/01/2024)21,5...

Rural Municipality of Hazelwood No. 94

Rural municipality in Saskatchewan, Canada Rural municipality in Saskatchewan, CanadaHazelwood No. 94Rural municipalityRural Municipality of Hazelwood No. 94Location of the RM of Hazelwood No. 94 in SaskatchewanCoordinates: 49°51′47″N 102°41′17″W / 49.863°N 102.688°W / 49.863; -102.688[1]CountryCanadaProvinceSaskatchewanCensus division1SARM division1Federal ridingSouris—Moose MountainProvincial ridingCanningtonMoosominFormed[2]January 1, 1...

 

Dopamine receptor

Class of G protein-coupled receptors Dopamine Dopamine receptors are a class of G protein-coupled receptors that are prominent in the vertebrate central nervous system (CNS). Dopamine receptors activate different effectors through not only G-protein coupling, but also signaling through different protein (dopamine receptor-interacting proteins) interactions.[1] The neurotransmitter dopamine is the primary endogenous ligand for dopamine receptors. Dopamine receptors are implicated in ma...

 

Court

Judicial institution with authority to resolve legal disputes For other uses, see Court (disambiguation). The examples and perspective in this article deal primarily with Western culture and do not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (December 2016) (Learn how and when to remove this message) A trial at the Old Bailey in London as drawn by Thomas Rowlandson and Augustus Pugin for ...

Fundamental theorem of arithmetic

Integers have unique prime factorizations Not to be confused with Fundamental theorem of algebra or Fundamental theorem of calculus. In Disquisitiones Arithmeticae (1801) Gauss proved the unique factorization theorem [1] and used it to prove the law of quadratic reciprocity.[2] In mathematics, the fundamental theorem of arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every integer greater than 1 can be represented uniquely ...

 

فلسفة مسيحية

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. جزء من سلسلة مقالات حولالثقافة المسيحية العمارة العمارة بيزنطية قوطية باروكية باروكية روكوكو عمارة الكنيسة الأثيوبية المظاهر الثقافية الفن الموسيقى الأدب الفلسفة المسرح ا...