Función xeradora
|
Read other articles:
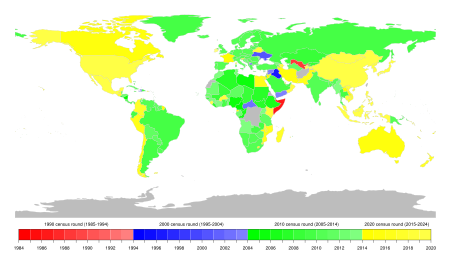
Peta dunia yang menunjukkan sensus negara terbaru pada tahun 2014 Sensus atau cacah jiwa adalah cara terstruktur untuk mendapatkan informasi deskriptif tentang jumlah dari sebuah populasi (tidak hanya populasi manusia). Sensus digunakan untuk demokrasi (pemilu), pengumpulan pajak, juga digunakan dalam ilmu (ekonomi). Di antaranya yang terbesar adalah sensus demografi, sensus pertanian, dan sensus ekonomi. Sensus beda dengan teknik sampling karena sampel hanya ambil statistik dari subset dari ...

A Free Soulposter rilis teatrikalSutradaraClarence BrownProduserClarence BrownIrving Thalberg (tidak disebutkan)Ditulis olehDialog lanjutan olehJohn MeehanAdaptation byBecky Gardiner[1]Tidak disebutkan:Philip DunningDorothy FarnumJohn LynchBerdasarkanA Free Soul (novel 1927)by Adela Rogers St. JohnsA Free Soul (permainan panggung 1928)by Willard Mack (tidak disebutkan)[1]PemeranNorma ShearerSinematograferWilliam DanielsPenyuntingHugh WynnPerusahaanproduksiMetro-Goldwyn-MayerDi...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (May 2016) (Learn how and when to remove this template message) This article may be confusing or unclear to readers. In particular, Lead section has to state the nature of ...

Istana MerdekaIstana Merdeka pada tahun 2010Location within JakartaInformasi umumGaya arsitekturArsitektur PalladianLokasiJalan Medan Merdeka Utara GambirJakarta 10160, IndonesiaKotaGambir, Gambir, Jakarta PusatNegaraIndonesiaKoordinat6°10′17.1″S 106°49′28.5″E / 6.171417°S 106.824583°E / -6.171417; 106.824583Mulai dibangun1873Desain dan konstruksiArsitekJacobus Bartholomeus Drossaers Istana Merdeka merupakan tempat resmi kediaman dan kantor Presiden Indones...

Berikut ini adalah genealogi yang dicatat di dalam Alkitab sejak manusia pertama, Adam diciptakan. Kitab Taurat Keturunan Adam dan Hawa Genealogi Adam hingga Nuh (Kejadian 4:17–22; 5:1–32; 1Tawarikh 1) Adam Hawa ...

Radio station in Malta–Albany, New York For the station known as WQBK-FM from 1972 to 2019, see WPBZ-FM. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: WQBK-FM – news · newspapers · books · scholar · JSTOR (February 2014) (Learn how and when to remove this message) WQBK-FMMalta, New YorkBroadcast areaCap...

Ираклеониты — ученики гностика Ираклеона (II век). Упоминаются как особая секта Епифанием и Августином; при крещении и миропомазании они соблюдали обряд помазания елеем и при этом произносили воззвания на арамейском языке, которые должны были освободить душу от власт�...

Cushitic language of Northeast Africa BejaBidhaawyeet, Tubdhaawi, تُبڈاوِNative toSudan, Eritrea, EgyptRegionRed SeaEthnicityBejaNative speakers2.76 million (2022–2023)[1]Language familyAfro-Asiatic CushiticNorthBejaDialectsHadendoa Hadareb Amarar Bisharin Beni-AmerWriting systemLatin alphabet (limited use)Arabic alphabet (limited use)Official statusRecognised minoritylanguage in Eritrea SudanLanguage codesISO 639-2bejISO 639-3bejGlottologbeja1238 Bej...

Large bag made of rough fiber, often used for storage and transport Potato sack redirects here. For the alternate reality game, see Potato Sack.This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Gunny sack – news · newspapers · books · scholar · JSTOR (July 2023) (Learn how and when to remove this message)Sack ...

La liste des épisodes de The Big Bang Theory, série télévisée américaine, est constituée de 279 épisodes. Panorama des saisons Saison Nombred'épisodes Diffusion originale Dates de sortie DVD Années Début de saison Fin de saison Zone 1(dont États-Unis) Zone 2(dont France) 1 17 2007-2008 (en) 24 septembre 2007 19 mai 2008 2 septembre 2008 3 mars 2010[1] 2 23 2008-2009 (en) 22 septembre 2008 11 mai 2009 15 septembre 2009 3 novembre 2010[2] 3 2009-2010 (en) 21 sep...
Video game franchise For other uses, see The Elder Scrolls (disambiguation). Video game seriesThe Elder ScrollsGenre(s)Action role-playingDeveloper(s)PrimaryBethesda Softworks (1994–1998)Bethesda Game Studios (2002–present)OtherVir2L Studios (2003–2004)TKO Software (2004)ZeniMax Online Studios (2014)Dire Wolf Digital (2017)Publisher(s)PrimaryBethesda Softworks (1994–present)2K Games (Oblivion only)OtherVir2L Studios (2003–2004)Nokia (2004)Platform(s)AndroidiOSJ2MEmacOSMicrosoft Wind...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Lightning Ridge redirects here. For the Ion Idriess book, see Lightning Ridge (book). Town in New South Wales, AustraliaLightning RidgeNew South WalesFossicking field in Lightning RidgeLightning RidgeCoordinates29°26′0″S 147°58′0″E / 29.43333°S 147.96667°E / -29.43333; 147.96667Population2,284 (2016 census)[1]Established1922Postcode(s)2834Elevation170 m (558 ft)Location 74 km (46 mi) N of Walgett 720 km (447 mi) NW...

This section tabulates the heads of qualification in a form suitable to be filled in as events progress. The full qualification rules[1] for basketball published by FIBA contain intricate conditions too lengthy for inclusion in Wikipedia. Basketball at the2024 Summer OlympicsBasketballQualificationmenwomenTournamentmenwomenRostersmenwomen3x3 basketballQualificationmenwomenTournamentmenwomenvte The women's 3x3 qualification for the Olympic basketball tournament occured between Novembe...

Kevin McNaughton McNaughton pada tahun 2011Informasi pribadiNama lengkap Kevin Paul McNaughton[1]Tanggal lahir 28 Agustus 1982 (umur 41)Tempat lahir Dundee, SkotlandiaTinggi 1,78 m (5 ft 10 in)Posisi bermain BekInformasi klubKlub saat ini Inverness Caledonian ThistleKarier senior*Tahun Tim Tampil (Gol)1999–2006 Aberdeen 175 (3)2006–2015 Cardiff City 254 (1)2013 → Bolton Wanderers (pinjaman) 13 (1)2014–2015 → Bolton Wanderers (pinjaman) 9 (0)2015–2016 W...

Bozner Bergsteigerlied (bahasa Indonesia: lagu pendaki Bozen) adalah salah satu dari dua lagu kebangsaan tidak resmi Tirol Selatan; lagu lainnya adalah Andreas-Hofer-Lied. Lirik lagu Bozner Bergsteigerlied disusun pada tahun 1926 oleh Karl Felderer di Moos am Ritten. Melodinya berasal dari lagu pengrajin kuno Tirol. Pada saat lagu ini digubah, kampanye Italianisasi Tirol Selatan yang dilancarkan oleh kaum fasis Italia tengah mencapai puncaknya, dan mereka melarang segala nama yang berkai...

Buyid amir of Iraq from 1027 to 1044 Jalal al-DawlaAmir of Iraq Amir al-umaraReign1027–1044PredecessorMusharrif al-DawlaSuccessorAbu KalijarBorn993 or 994DiedMarch 1044IssueAl-Malik al-AzizAbu Mansur AliUnnamed daughterNamesLaqab: Jalal al-DawlaKunya: Abu TahirGiven name: Firuz KhusrauFatherBaha' al-DawlaReligionShia Islam Abu Tahir Firuz Khusrau (Persian: ابوطاهر فیروزخسرو), better known by his laqab of Jalal al-Dawla (993 or 994 – March 1044), was the Buyid amir of Iraq ...

Centered figurate number that represents a decagon with a dot in the center A centered decagonal number is a centered figurate number that represents a decagon with a dot in the center and all other dots surrounding the center dot in successive decagonal layers. The centered decagonal number for n is given by the formula 5 n 2 − 5 n + 1 {\displaystyle 5n^{2}-5n+1\,} Thus, the first few centered decagonal numbers are 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051,...

Artikel ini bukan mengenai Dinasti Tang. Tang Tang adalah peralatan bengkel yang khusus digunakan untuk memegang, memotong, melepas, dan memasang bahan kerja.[1] Jenis tang bermacam-macam, di antaranya tang kombinasi, tang lancip, dan tang potong.[2] Jenis Tang kombinasi Tang kombinasi digunakan untuk memegang, memuntir dan memotong benda kerja, misal kawat penghantar (kabel). Ciri utama dari tang kombinasi adalah:[3] Ujung rahangnya mempunyai pinggiran yang bergerigi ...








![{\displaystyle [x^{n}]f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f412f2030aac7b4cabca1ba9bd0b7d8498df4e95)

![{\displaystyle [x^{n}]e^{x}=1/n!;\quad [u^{m}](1+u)^{s}={\binom {s}{m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da4c223bee880999bc06852792b396c8f60dabe2)




![{\displaystyle b_{n}:=[x^{n}]\operatorname {LG} (a_{n};x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/545c302a68d78c5b29be0ee431163be4aa0e726a)

![{\displaystyle [x^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4821eb01b0a71990397ce457335c56615c669b18)


















![{\displaystyle {\begin{aligned}&z^{m}G(z)=\sum _{n=m}^{\infty }g_{n-m}z^{n}\\[4px]&{\frac {G(z)-g_{0}-g_{1}z-\cdots -g_{m-1}z^{m-1}}{z^{m}}}=\sum _{n=0}^{\infty }g_{n+m}z^{n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3052ce87c17f67792fcf7588a5cc631e826b027c)
![{\displaystyle {\begin{aligned}G'(z)&=\sum _{n=0}^{\infty }(n+1)g_{n+1}z^{n}.\\[4px]z\cdot G'(z)&=\sum _{n=0}^{\infty }ng_{n}z^{n}.\\[4px]\int _{0}^{z}G(t)\,dt&=\sum _{n=1}^{\infty }{\frac {g_{n-1}}{n}}z^{n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a9b025f85ed0103276d7a5d28e6938068722e26)




