Oubli de la fréquence de base
|
Read other articles:

June HaverJune Haver, 1946LahirJune Stovenour(1926-06-10)10 Juni 1926Rock Island, Illinois, A.S.Meninggal4 Juli 2005(2005-07-04) (umur 79)Brentwood, Los Angeles, California, A.S.Tahun aktif1941–1953Suami/istri Jimmy Zito (m. 1947; c. 1948) Fred MacMurray (m. 1954; meninggal 1991) Anak2 June Haver (nee June Stovenour, 10 Juni 1926 – 4 Juli 2005) adalah seorang ak...
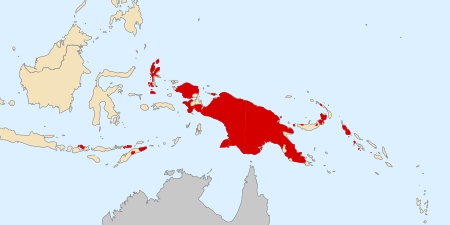
لغات بابوامعلومات عامةصنف فرعي من لغة بشرية البلد إندونيسيابابوا غينيا الجديدةجزر سليمان السكان الأصليون لـ بابواويونNorth Halmahera peoples (en) Alor–Pantar peoples (en) عدد المتحدثين 4٬600٬000 تعديل - تعديل مصدري - تعديل ويكي بيانات توزيع اللغات البابوية باللون الأحمر. يطلق اسم لغات البابوا Papuan...

Chemical compound Not to be confused with 5F-AB-PINACA. 5F-APINACAClinical dataOther names5F-AKB-48, 5F-AKB48Legal statusLegal status BR: Class F2 (Prohibited psychotropics)[1] CA: Schedule II DE: Anlage II (Authorized trade only, not prescriptible) UK: Class B US: Schedule I UN: Psychotropic Schedule II[2] Identifiers IUPAC name N-(adamantan-1-yl)-1-(5-fluoropentyl)-1H-indazole-3-carboxamide CAS Number1400742-13-3PubChem CID71711119ChemSpide...

American politician (1857–1945) Choice Boswell RandellMember of theU.S. House of Representativesfrom TexasIn officeMarch 4, 1901 – March 3, 1913Preceded byJoseph W. BaileySucceeded bySam RayburnConstituency5th district (1901–1903)4th district (1903–1913)Grayson County AttorneyIn office1882–1888Denison City AttorneyIn office1882–1882 Personal detailsBorn(1857-01-01)January 1, 1857Murray County, Georgia, USDiedOctober 19, 1945(1945-10-19) (aged 88)Sherman, Texas, USPol...

Bank Notes Tax Act 1910Parliament of Australia Long title An Act to impose a Tax upon Bank Notes. CitationNo. 14 of 1910Royal assent10 October 1910Repealed21 August 1945Repealed byCommonwealth Bank Act 1945Status: Repealed The Bank Notes Tax Act 1910 (Cth) was an Act of the Parliament of Australia which imposed a prohibitive tax on banknotes issued by banks in Australia.[1][2] The Act was enacted in October 1910 by the Fisher Labour Government under Section 51 (xii) of the Co...

Coptic OrphansAbbreviationCOFormation1988; 36 years ago (1988)FounderNermien RiadTypenonprofitHeadquartersFairfax, Virginia, United StatesArea served EgyptWebsitehttps://copticorphans.org/ Coptic Orphans Support Association, better known as Coptic Orphans (CO) is an international development organization that has transformed the lives of over 86,000 children in Egypt since 1988. Its mission is to break the cycle of poverty through long-term programs that focus on education.&...

Mario Desiati nel 2018 al Festival internazionale del giornalismo di Perugia Premio Strega 2022 Mario Desiati (Locorotondo, 13 maggio 1977) è uno scrittore, poeta e giornalista italiano. Indice 1 Biografia 2 Opere principali 2.1 Prosa 2.2 Poesia 2.3 Curatele 2.4 Premi e riconoscimenti 3 Note 4 Altri progetti 5 Collegamenti esterni Biografia Nato a Locorotondo (Bari) nel 1977[1], ma cresciuto nella vicina Martina Franca (in provincia di Taranto)[2], risiede stabilmente a Roma,...

Capture of the Jeune RichardPart of the Napoleonic WarsCaptain William Rogers Capturing the 'Jeune Richard', 1 October 1807, Samuel DrummondDate1 October 1807Locationoff Barbados, Caribbean SeaResult British victoryBelligerents United Kingdom FranceCommanders and leaders William Rogers UnknownStrength 1 packet ship 1 privateerCasualties and losses 13 killed and wounded 54 killed and wounded1 privateer capturedvteWest Indies campaign (1803–1810) Saint-Domingue St Lucia • Tobag...

Nestor El Maestro Nazionalità Serbia Inghilterra Calcio Ruolo Allenatore Squadra CSKA Sofia Carriera Squadre di club1 2014 Hollabrunn? (?) Carriera da allenatore 2001-2002 West Ham Utd(Coll. tecnico)2002-2004 Austria Vienna(Giov.)2004-2006 Valencia(Giov.)2006-2008 Schalke 04(Vice)2010-2013 Hannover 96(Vice)2014 Amburgo(Vice)2016-2017 Austria Vienna(Coll. tecnico)2017-2018 Spartak Trnava2018-2019 CSKA Sofia2019-2020 Sturm Gra...

Азорские островапорт. Açores Почтовая марка номиналом в 25 реалов, Ангра, 1892 (Sc #2) Почтовые администрации 1868—1912 1 мильрейс = 1000 рейсов или реалов с 1912 1 эскудо = 100 центаво с 2002 1 евро = 100 центов Первые почтовые марки Стандартная 1868 Полупочтовая 1911 Доплатная 1904 Газетная 1876 Фила...

Pour l’article homonyme, voir Ladra. Marché aux puces Feira da Ladra à Lisbonne. La Feira da Ladra, littéralement Marché de la Voleuse, est un marché aux puces qui se tient à Lisbonne, dans plusieurs rues du Campo de Santa Clara, à l'est de l'Alfama. Initialement, ce marché a ses racines au Moyen Âge, où les commerçants vendaient leurs produits et aussi des objets volés (comme son nom l'indique). De nos jours c'est un marché très réputé, qui malgré son nom garde une grande...

Russian footballer Magomed Adiyev Adiyev coaching Anzhi Makhachkala in 2019Personal informationFull name Magomed Musayevich AdiyevDate of birth (1977-06-30) 30 June 1977 (age 46)Place of birth Grozny, Russian SFSR, Soviet UnionHeight 1.88 m (6 ft 2 in)Position(s) ForwardTeam informationCurrent team Kazakhstan (manager)Akhmat Grozny (manager)Youth career Terek Grozny RSDYuShOR-2 MakhachkalaSenior career*Years Team Apps (Gls)1994 Ingushetiya Nazran 14 (1)1995 Anzhi-2 Makhach...

South African politician (born 1980) Pule MabeNational Spokesperson of the African National CongressIn office6 February 2018 – 28 January 2023PresidentCyril RamaphosaPreceded byZizi KodwaSucceeded byMahlengi BhenguMember of the National Assembly of South AfricaIn office21 May 2014 – 31 August 2017 Personal detailsBornPuleng Peter Mabe19 March 1980Phalaborwa, TransvaalSouth AfricaPolitical partyAfrican National CongressAlma mater Tshwane University of Technology Universit...

شهدت دول العالم خلال الفترة (1950-1990م) تزايداً سكانياً سريعاً رافقه تدفق مستمر للسكان من الريف إلى المدن واكتظاظ للسكان فيها، وتوسع عمراني على حساب الأراضي الزراعية، ويتوقع العلماء أن يكون لهذا التزايد السكاني آثاره الواضحة على الحياة الاجتماعية والاقتصادية في السنوات الم�...

Pioneering French aviator Louis Paulhan in 1909 Isidore Auguste Marie Louis Paulhan (French: [pɔlɑ̃]; 19 July 1883 – 10 February 1963),[1] was a French aviator. He is known for winning the first Daily Mail aviation prize for the first flight between London and Manchester in 1910. Biography Paulhan was born at Pézenas, Hérault, and his heavier-than-air flying career began with making model aircraft. Stationed at St Cyr as a balloon pilot during his military service, in 1...

Glen CoulthardCoulthard in 2013BornGlen Sean Coulthard1974 (age 49–50)NationalityCanadianAcademic backgroundAlma materUniversity of VictoriaThesisSubjects of Empire? (2009)Doctoral advisorJames TullyOther advisorsTaiaiake AlfredInfluencesFrantz FanonAcademic workDisciplineIndigenous studiesphilosophypolitical scienceSchool or traditionMarxismMain interestsIndigenous sovereigntyanti-colonialismNotable worksRed Skin, White Masks (2014)Notable ideasGrounded normativity Glen Sean ...

Not to be confused with Dubai Marina Mall. Very large shopping mall in Dubai, UAE 25°11′51″N 55°16′45″E / 25.19750°N 55.27917°E / 25.19750; 55.27917 Dubai Mallدبي مولThe exterior of the Dubai Mall (2023)LocationDowntown Dubai,United Arab EmiratesAddressDubai downtownOpening date4 November 2008; 15 years ago (2008-11-04)DeveloperEmaar PropertiesManagementEmaar Malls GroupArchitectDP ArchitectsNo. of stores and services1,200+No. of anc...

Musical instrument MellotronA Mellotron Mk VIManufacturerBradmatic/Mellotronics (1963–70)Streetly Electronics (1970–86, 2007–present)Dates1963 (Mk I)1964 (Mk II)1968 (M300)1970 (M400)2007 (M4000)Technical specificationsPolyphonyFullOscillatorAudio tapeSynthesis typeSample-based synthesisInput/outputKeyboard1 or 2 × 35 note manuals (G2–F5) The Mellotron is an electro-mechanical musical instrument developed in Birmingham, England, in 1963. It is played by pressing its keys, each of whi...
Abtswind Lambang kebesaranLetak Abtswind NegaraJermanNegara bagianBayernWilayahUnterfrankenKreisKitzingenMunicipal assoc.Wiesentheid Pemerintahan • MayorKlaus LenzLuas • Total12,81 km2 (495 sq mi)Ketinggian291 m (955 ft)Populasi (2013-12-31)[1] • Total850 • Kepadatan0,66/km2 (1,7/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos97355Kode area telepon09383Pelat kendaraanKTSitus webwww.abtswind.de Abtswind ada...

American computer scientist (born 1936) Richard Edwin StearnsRichard Stearns in 2009Born (1936-07-05) July 5, 1936 (age 88)Caldwell, New JerseyAlma materCarleton College (B.A.) Princeton University (Ph.D.)AwardsACM Turing Award (1993)Frederick W. Lanchester Prize (1995)Scientific careerInstitutionsUniversity at AlbanyDoctoral advisorHarold W. Kuhn Richard Edwin Stearns (born July 5, 1936) is an American computer scientist who, with Juris Hartmanis, received the 1993 ACM Turing Award...
