Matrice symétrique
|
Read other articles:

Templat:Alevism Pir Sultan Abdal (sekitar1480–1550) adalah seorang penyair Alevi Turki, yang bahasanya yang tajam dan jelas serta kekayaan imajinasi serta keindahan syair-syairnya membuat ia dicintai oleh rakyat Turki. Pir Sultan Abdal mencerminkan kehidupan sosial, budaya, dan keagamaan rakyat. Ia adalah seorang humanis dan menulis tentang perlawanan, cinta, perdamaian, kematian, dan Tuhan. Ia juga memberontak melawan pemerintahan yang otoriter yang menyebabkan ia mengalami masalah dengan ...

Santo dan martir Engelbert dari Köln Patung Uskup Agung Engelbert di Puri Burg Comte Engelbert II dari Berg, juga dikenal sebagai Santo Engelbert, Engelbert dari Köln, Engelbert I atau Engelbert I dari Berg (1185 atau 1186, Schloss Burg – 7 November 1225, Gevelsberg) merupakan seorang Uskup Agung dan Santo;[a] ia terkenal karena dibunuh oleh anggota keluarganya sendiri. Catatan ^ The description Engelbert I of Berg can refer either to Count Engelbert I of Berg or to the subject of...

Dalam artikel ini, pertama atau paternal nama keluarganya adalah Olmos dan nama keluarga maternal atau keduanya adalah Dick. Giuliana OlmosOlmos di Prancis Terbuka 2021Nama lengkapGiuliana Marion Olmos DickKebangsaan MeksikoTempat tinggalFremont, Amerika SerikatLahir04 Maret 1993 (umur 31)Schwarzach im Pongau, AustriaTinggi170 cm (5 ft 7 in)Memulai pro2018Tipe pemainKanan (backhand dua tangan)KampusUniversity of Southern CaliforniaTotal hadiahUS $1.130.043Tung...
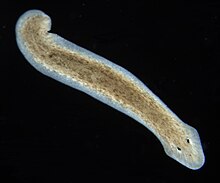
Planaria Dugesia subtentaculata, seekor dugesiidae. Klasifikasi ilmiah Kerajaan: Animalia Filum: Platyhelminthes Kelas: Rhabditophora Ordo: TricladidaLang, 1884 Subordo Maricola Cavernicola Continenticola Planaria termasuk dalam Filum Platyhelminthes yang memiliki bentuk tubuh pipih dan simetri bilateral. Planaria berhabitat di daerah bertemperatur 18–24 °C dengan ketinggian antara 500–1500 m dpl. Tubuh planaria tersusun dari bagian cranial, trunchus dan caudal. Bagian cranial terd...

دوري الولايات المتحدة - البطولة الموسم الحاليبطولة الدوري الأمريكي 2019 الافتتاح 2011 تاريخ الإنشاء 2011 الرياضة كرة القدم البلد الولايات المتحدة و كندا عدد الفرق 36 فريق الأكثر فوزا لويسفيل سيتي الصعود الدوري الأمريكي لكرة القدم هبوط بطولة الدوري الأمريكي الدرجة ...

Class of people in the middle of a societal hierarchy For the band, see Middle Class (band).Not to be confused with Working class.Global shareholders of wealth by wealth group, Credit Suisse, 2021 The middle class refers to a class of people in the middle of a social hierarchy, often defined by occupation, income, education, or social status. The term has historically been associated with modernity,[1] capitalism and political debate.[2] Common definitions for the middle class...

American baseball playerFor the South African politician, see Mark Lowe (politician).Baseball player Mark LoweLowe with the Toronto Blue JaysPitcherBorn: (1983-06-07) June 7, 1983 (age 40)Houston, Texas, U.S.Batted: LeftThrew: RightMLB debutJuly 7, 2006, for the Seattle MarinersLast MLB appearanceSeptember 23, 2016, for the Detroit TigersMLB statisticsWin–loss record10–27Earned run average4.22Strikeouts352 Teams Seattle Mariners (2006–2010) Texas Range...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Let Go for LoveSutradaraAman ChangPemeranChapman ToCharlene ChoiTanggal ri...

2008 single by Giò Di Tonno and Lola PonceColpo di fulmineSingle by Giò Di Tonno and Lola PonceB-sideColpo di fulmine (Instrumental)ReleasedFebruary 2008LabelMusiZaSongwriter(s)Gianna NanniniAudioColpo di fulmine on YouTube Colpo di fulmine (transl. Love at first sight) is a 2008 song composed by Gianna Nannini and performed by Giò Di Tonno and Lola Ponce. It won the 58th edition of the Sanremo Music Festival. Background The song was originally composed by Nannini for her rock opera Pia de...

Consolidated VulteeConvair Création 1943 Disparition 1996 Fondateurs Thomas Oliver Forme juridique Société par actions Siège social San Diego, Californie États-Unis Activité Militaire, Défense Produits Avions, missiles Société mère Consolidated Aircraft Vultee Aircraft Filiales Consairways (en) Effectif 127 Fonds propres 213.5 millions de $ Chiffre d'affaires 128 millions de $ modifier - modifier le code - voir Wikidata Le Convair XF-92A a été le premier avion américa...

County of England Staffs redirects here. For other uses, see Staff (disambiguation). Ceremonial county in EnglandStaffordshireCeremonial countyThe Sherbrook Valley in Cannock Chase; a bottle kiln in Longton, Stoke-on-Trent; and Lichfield CathedralStaffordshire within EnglandCoordinates: 52°48′25″N 02°06′58″W / 52.80694°N 2.11611°W / 52.80694; -2.11611Sovereign stateUnited KingdomConstituent countryEnglandRegionWest MidlandsEstablishedAncientTime zoneUTC+0 (...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Casa Pia – news · newspapers · books · scholar · JSTOR (September 2010) (Learn how and when to remove this message) The Castle of São Jorge, Casa Pia's first location The Casa Pia is a Portuguese institution founded by Maria I, known as A Pia (Mary the Pious), and organized by ...

Railway station in West Bengal, India Bansberia Indian Railways station and Kolkata Suburban Railway stationBansberia railway station (Regd as BANSH BARIA in the Indian railway directory)General informationLocationStation Road, Bansberia, Hooghly district, West BengalIndiaCoordinates22°57′26″N 88°23′43″E / 22.957168°N 88.395239°E / 22.957168; 88.395239Elevation13 metres (43 ft)Owned byIndian RailwaysOperated byEastern RailwayLine(s)2Platforms3Tracks2Co...

Former flying squadron of the Royal Air Force No. 259 Squadron RAFActive20 August 1918 – 14 January 1919 16 February 1943 – 1 May 1945Country United KingdomBranch Royal Air ForceMotto(s)Swahili: Haya ingia napigane(Get in a fight)InsigniaSquadron BadgeAn eagle head over a globeSquadron CodesVP (Apr 1939 – Sep 1939)Military unit No. 259 Squadron RAF was a Royal Air Force Squadron formed in Africa as a reconnaissance and anti-submarine unit in World War II. History World Wa...

تصنيف فيفا العالمي للرجالمعلومات عامةالرياضة كرة القدم المُؤَلِّف الاتحاد الدولي لكرة القدم تاريخ البدء أغسطس 1993 تعريف الصيغة Opposition strength multiplier = ( 200 − ranking position ) / 100 {\displaystyle {\text{Opposition strength multiplier}}=({200-{\text{ranking position}})/100}} موقع الويب fifa.com… (الإنجليزية) تعديل - تعديل مصدري - تع...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2020) جائزة ستيريا الكبرى 2020 (بالألمانية: Formula 1 Pirelli Großer Preis der Steiermark 2020) السباق 2 من أصل 17 في بطولة العالم ...

Outdoor clothing and equipment retailer Eastern Mountain Sports, Inc.Company typeSubsidiaryIndustryRetailFounded1967; 57 years ago (1967)FounderAlan McDonough & Roger FurstHeadquartersMeriden, Connecticut, United StatesNumber of locations24Area servedUnited StatesProductsOutdoor gear and clothingParentGoDigital Media Group (2022–present)Websiteems.com Eastern Mountain Sports (or EMS) is an outdoor clothing and equipment retailer in the Northeastern United States headqu...

Men's canoe sprint C-1 1000 metresat the Games of the XXXI OlympiadVenueLagoa StadiumDate15–16 August 2016Competitors19 from 19 nationsWinning time3:56.926Medalists Sebastian Brendel Germany Isaquias Queiroz Brazil Ilia Shtokalov Russia← 20122020 → Canoeing at the2016 Summer OlympicsList of canoeistsQualificationSlalomC-1menC-2menK-1menwomenSprintC-1 200 mmenC-1 1000 mmenC-2 1000 mmenK-1 200 mmenwomenK-1 500 mwomenK-1 1000 mmenK-2 200 mmenK-...

Hungarian politician Pál OrdódyMinister of Public Works and TransportIn office24 April 1880 – 9 August 1882Preceded byGyula SzapárySucceeded byGábor Kemény Personal detailsBorn(1822-08-26)26 August 1822Pest, HungaryDied26 August 1885(1885-08-26) (aged 63)Bad Ischl, Austria-HungaryPolitical partyDeák PartyLiberal PartyProfessionpolitician The native form of this personal name is ordódi és rozsonmiticzi Ordódy Pál. This article uses Western name order when mentioni...








































![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![{\displaystyle [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f637a17dac262ee0fc8d58e31d08ca3ebe5a0fed)
![{\displaystyle \forall \,x,y\in \mathbb {R} ^{n}:\qquad x^{\mathsf {T}}y\leqslant [x]^{\mathsf {T}}[y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a457946928ce09c162462d7a5f8d6029f5acc218)


