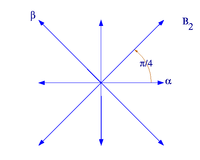
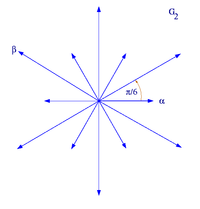
Système de racines
|
Read other articles:

BerlinTokoh Money HeistPenampilanperdanaDo as Planned (2017)PenampilanterakhirAn Endangered Elephant (2023)PenciptaÁlex PinaPemeranPedro AlonsoInformasiNama lengkapAndrés de FonollosaAliasBerlinSimon Martínez (dalam seri televisi Berlin)PekerjaanPerampok Besar, Ahli BobolSenjataM16M1911KeluargaProfesor Sergio Marquina (saudara laki-laki)Raquel Murillo Lisbon (saudara ipar perempuan)PasanganTatiana Marse (cerai)AnakRafael de Fonollosa (anak laki-laki)KewarganegaraanSpanyol Berlin ( Andrés ...

American football player (born 1965) For other people with similar names, see Chris Carter (disambiguation). American football player Cris CarterCarter in 2014No. 80, 88Position:Wide receiverPersonal informationBorn: (1965-11-25) November 25, 1965 (age 58)Troy, Ohio, U.S.Height:6 ft 3 in (1.91 m)Weight:208 lb (94 kg)Career informationHigh school:Middletown (Middletown, Ohio)College:Ohio State (1984–1986)Supplemental draft:1987 / Round: 4Career history...

The President, Council, and Fellows of the Royal Society of London for Improving Natural KnowledgeTanggal pendirianNovember 1660Kantor pusatLondon, Britania RayaJumlah anggota 5 Anggota Kerajaan1450 Anggota140 Anggota Luar NegriPresidentSir Paul NurseSitus webwww.royalsociety.org The Royal Society of London for the Improvement of Natural Knowledge, atau yang lebih dikenal dengan sebutan Royal Society saja, adalah perkumpulan yang didirikan pada tahun 1660 dengan tujuan memajukan ilmu pengetah...

Sporting event delegationSouth Korea at the1992 Summer OlympicsIOC codeKORNOCKorean Olympic CommitteeWebsitewww.sports.or.kr (in Korean and English)in BarcelonaCompetitors226 (154 men, 72 women) in 24 sportsFlag bearer Kim Tae-hyunMedalsRanked 7th Gold 12 Silver 5 Bronze 12 Total 29 Summer Olympics appearances (overview)19481952195619601964196819721976198019841988199219962000200420082012201620202024 South Korea competed as Korea at the 1992 Summer Olympics in Barcelona, Spain. 226 c...

Questa voce o sezione sull'argomento competizioni calcistiche non è ancora formattata secondo gli standard. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Coppa della Germania Est 1964-1965FDGB Pokal 1964-1965 Competizione Coppa della Germania Est Sport calcio Edizione 14ª Luogo Germania Est Risultati Vincitore Aufbau Magdeburgo Secondo Motor Jena Cronologia della competizione 1963-1964 1964-1965 Manuale La Coppa...

Angelo Alessio Alessio pada 2012Informasi pribadiTanggal lahir 29 April 1965 (umur 58)Tempat lahir Capaccio, ItaliaTinggi 181 cm (5 ft 11 in)Posisi bermain Sayap KananKarier senior*Tahun Tim Tampil (Gol)1984–1987 Avellino 48 (7)1987–1992 Juventus 99 (11)1988–1989 → Bologna (pinjaman) 29 (4)1992–1995 Bari 77 (12)1995–1997 Cosenza 57 (15)1997 Avellino 5 (1)1997–1998 Modena 18 (1)Kepelatihan2002 Napoli (asisten)2003 Napoli (asisten)2004–2005 Imolese2006–200...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (janvier 2023). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? C...

1779 philosophical work by David Hume Title page David Hume Dialogues Concerning Natural Religion is a philosophical work by the Scottish philosopher David Hume, first published in 1779. Through dialogue, three philosophers named Demea, Philo, and Cleanthes debate the nature of God's existence. Whether or not these names reference specific philosophers, ancient or otherwise, remains a topic of scholarly dispute. While all three agree that a god exists, they differ sharply in opinion on God's ...

Leopold-Handgriff Pemeriksaan Leopold adalah cara untuk meraba bagian rahim wanita hamil secara teratur. Metode ini sederhana, murah, dan tidak melibatkan prosedur invasif. Tujuannya adalah untuk menentukan di mana posisi, presentasi, dan letak janin di dalam rahim. Materi ini menjelaskan empat langkah pemeriksaan Leopold dan cara penggunaannya untuk mengetahui cara janin berada dalam trimester ketiga kehamilan.[1] Tujuan Berikut ini tujuan dalam pemeriksaan Leopold. Menjelaskan cara ...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) بوليفيا في الألعاب الأولمبية علم بوليفيا رمز ل.أ.د. BOL ل.أ.و. اللجنة الأولمبية البوليفية تاريخ �...

Former Danish sugar factory The former factory in 2013 Højbygaard Sugar Factory (Danish: Højbygaard Sukkerfabrik) was built in 1872–74 at Holeby on Lolland in southeastern Denmark. It was one of the first modern sugar factories built for the country's emerging sugar beet industry. It was taken over by De Danske Sukkerfabrikker in 1877 and operated until 1959. The buildings were then acquired by De Forenede Papirfabrikker (United Paper Mills) and operated as a paper mill under the name Hø...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1744 in Canada – news · newspapers · books · scholar · JSTOR (October 2021) (Learn how and when to remove this message) ← 1743 1742 1741 1744 in Canada → 1745 1746 1747 Decades: 1720s 1730s 1740s 1750s 1760s See also: History of Canada Timeline of ...

American soccer player (born 1982) Landon Donovan Donovan playing for LA Galaxy in 2010Personal informationFull name Landon Timothy DonovanDate of birth (1982-03-04) March 4, 1982 (age 42)Place of birth Ontario, California, United StatesHeight 5 ft 8 in (1.73 m)[1]Position(s) Winger, forwardYouth career1999 IMG AcademySenior career*Years Team Apps (Gls)1999–2000 Bayer Leverkusen II 28 (9)2000–2005 Bayer Leverkusen 7 (0)2001–2004 → San Jose Earthquakes (loan...

Local government elections in Dorset, England Bournemouth, Christchurch and Poole Council is a unitary authority in Dorset, England. It was formed in April 2019, with the inaugural elections held in May of that year. The council is made up of 76 councillors from 33 wards, elected for a four-year term, with the next elections due take place in 2027. Result maps Results of the 2019 election Results of the 2023 election Council elections 2019 Bournemouth, Christchurch and Poole Council election ...

كأس القارات 1997الحدثكأس القارات 1997 البرازيل أستراليا 6 0 التاريخ21 ديسمبر 1997الملعبملعب الملك فهد الدولي، الرياضالحكم بيروم أون-براسرت (الأتحاد التايلاندي)الحضور65,000 → 1995 1999 ← نهائي بطولة فيفا لكأس القارات 1997 لكرة القدم لتحديد الفائز في بطولة كأس القارات 1997 أقيم في استاد الم...

Reservoir in England Tring ReservoirsSite of Special Scientific InterestStartops End ReservoirLocationHertfordshireBuckinghamshireGrid referenceSP919136SP905131InterestBiologicalArea106.5 hectaresNotification1987Location mapMagic Map Tring Reservoirs is a group of four reservoirs close to Tring on the border of Hertfordshire and Buckinghamshire, England. Their purpose is to feed the Grand Union Canal.[1] The four reservoirs are: Startops End, Marsworth, Tringford and Wilstone. The fir...

American actor (1928–1982) Warren OatesOates in 1963BornWarren Mercer Oates(1928-07-05)July 5, 1928Depoy, Kentucky, U.S.DiedApril 3, 1982(1982-04-03) (aged 53)Los Angeles, California, U.S.OccupationActorYears active1953–1982Spouses Teddy Louise Farmer (m. 1959; div. 1966) Vickery Turner (m. 1969; div. 1974) Judy A. Jones (m. 1977) Childre...

Disambiguazione – Se stai cercando l'omonima area naturale protetta, vedi Lago di Osiglia (area protetta). Lago di OsigliaStato Italia Regione Liguria Provincia Savona ComuneOsiglia Coordinate44°17′52.72″N 8°11′56.44″E44°17′52.72″N, 8°11′56.44″E Altitudine637 m s.l.m. DimensioniLunghezza3 km Larghezza0,2 km Profondità massima65 m Volume0,013 km³ IdrografiaBacino idrograficoartificiale km² Immissari principaliOsigliett...

Census-designated place in Washington, United StatesEaston, WashingtonCensus-designated placeEaston as seen from the west sideLocation of Easton, WashingtonCoordinates: 47°14′18″N 121°10′42″W / 47.23833°N 121.17833°W / 47.23833; -121.17833CountryUnited StatesStateWashingtonCountyKittitasArea • Total3.22 sq mi (8.34 km2) • Land3.21 sq mi (8.31 km2) • Water0.02 sq mi (0.04 km2)E...