Sous-espace vectoriel
|
Read other articles:
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of Nepali musical instruments – news · newspapers · books · scholar · JSTOR (November 2020) (Learn how and when to remove this template message) Newar merchants of Kathmandu, Nepal parading in Lhasa, Tibet playing drums in 1903. This list contains traditi...

Cet article est une ébauche concernant une architecte espagnole. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Carme PigemBiographieNaissance 18 avril 1962 (61 ans)OlotNationalité espagnoleFormation École technique supérieure d'architecture du Vallès (d)Activité ArchitecteAutres informationsA travaillé pour École polytechnique fédérale de ZurichMembre de RCR ArquitectesDistinctions Prix Pritzker...

James IV beralih ke halaman ini. Untuk Lihat pula James IV dari Majorca, lihat James IV (disambiguasi). James IVRaja SkotlandiaBerkuasa11 Juni 1488 – 9 September 1513Penobatan24 Juni 1488PendahuluJames IIIPenerusJames VInformasi pribadiKelahiran(1473-03-17)17 Maret 1473Istana Stirling, Stirling, SkotlandiaKematian9 September 1513(1513-09-09) (umur 40)Pertempuran Flodden, Northumberland, InggrisWangsaStewartAyahJames III dari SkotlandiaIbuMargaret dari DenmarkPasanganMargaret TudorAnaks...
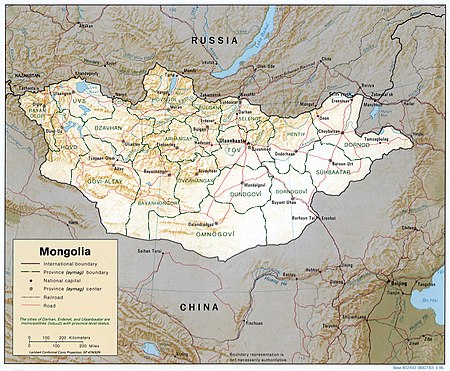
جمهورية منغوليا جمهورية منغوليا منغولياعلم منغوليا منغولياشعار منغوليا الشعار الوطني(بالإنجليزية: Go Nomadic, Experience Mongolia) النشيد: النشيد الوطني لمنغوليا [لغات أخرى] الأرض والسكان إحداثيات 46°N 105°E / 46°N 105°E / 46; 105 [1] أعلى قمة قمة خويت...

Ace Combat 2 Seni kotak Amerika UtaraPublikasiJP: 30 Mei 1997NA: 21 Agustus 1997EU: 24 Oktober 1997GenreSimulasi penerbangan tempurKarakteristik teknisPlatformPlayStation ModePermainan video pemain tunggal FormatCD-ROM Format kode Daftar 30 Informasi pengembangPengembangNamcoPenyuntingNamco DesainerMasanori KatoKomponisKohta TakahashiNobuhide IsayamaHiroshi OkuboTetsukazu NakanishiPenerbitWW: NamcoEU: Sony Computer EntertainmentPenilaianESRB Informasi tambahanMobyGamesace-combat-2 Bagian dari...

Voce principale: Impero ottomano. Mappa che illustra la decadenza dell'Impero Ottomano La dissoluzione dell'Impero ottomano (1908-1922) iniziò con la rivoluzione dei Giovani Turchi e con la Seconda era costituzionale che ripristinò la costituzione ottomana del 1876 e introdusse una politica multipartitica con un sistema elettorale in due fasi (legge elettorale) sotto il parlamento ottomano. La costituzione offriva speranza, liberando i cittadini dell'Impero, di modernizzare le istituzioni ...

Vishwamitra Gurukul of the Ancient Mithila University Vishwamitra Ashram, Bisaulविश्वामित्र आश्रमSymbolic image - Disciples Lord Rama and Lord Lakshmana performing guru-seva by pressing Vishvamitra's feet and legs (bazaar art, mid-1900's)Monastery informationFull nameShree Ram - Lakhan - Vishwamitra Bishram AshramOther namesSundar SadanEstablishedTreta YugaDedicated toIndian philosophy, Gayatri MantraCelebration dateMithila Madhya ParikramaPeopleFounder(s)Vishw...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Prison riot in Huntsville, Texas The Huntsville Unit, the location of the siege The 1974 Huntsville Prison siege was an eleven-day prison uprising that took place from July 24 to August 3, 1974, at the Huntsville Walls Unit of the Texas Department of Corrections in Huntsville, Texas. The standoff was one of the longest hostage-taking sieges in United States history.[1] Siege From July 24 to August 3, 1974, Federico Fred Gomez Carrasco and two other inmates laid siege to the education/...

Environmental news website Not to be confused with Mangabey. Mongabay CorporationFounded1999FounderRhett Ayers ButlerType501(c)(3)Tax ID no. 45-3714703FocusConservation journalismLocation1259 El Camino Real #150, Menlo Park, CA, USArea served GlobalKey peopleCEO Rhett Ayers ButlerRevenue Donations, grants, and advertisingEmployees 90 (Sep 2023)Websitemongabay.com Mongabay (mongabay.com) is an American conservation news web portal that reports on environmental science, energy, and green design...

Since 2023 These are tables of congressional delegations from South Carolina to the United States House of Representatives and the United States Senate. The current dean of the South Carolina delegation is Representative Jim Clyburn (SC-6), having served in the House since 1993. U.S. House of Representatives Main article: List of United States representatives from South Carolina Current members The current U.S. House delegation from South Carolina has 7 members, including 6 Republicans and 1...

Separation of church and state in France You can help expand this article with text translated from the corresponding article in French. (January 2017) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machin...

2008 video gameCivilization IV: ColonizationNorth American cover artDeveloper(s)Firaxis GamesPublisher(s)2K Games (Win)Aspyr (Mac)Designer(s)H. Edward PiperSeriesCivilizationEngineGamebryoPlatform(s)Microsoft Windows, Mac OS XReleaseMicrosoft WindowsNA: September 23, 2008[1]PAL: September 26, 2008[1]Mac OS XNA: December 22, 2009[2]EU: May 12, 2010Genre(s)Turn-based strategyMode(s)Single-player, multiplayer Sid Meier's Civilization IV: Colonization is a remake of the 1...

علاج طفلان يتلقيان علاجا للشلل. معلومات عامة من أنواع إجراء طبي التاريخ وصفها المصدر الموسوعة البريطانية نسخة سنة 1911 تعديل مصدري - تعديل العلاج طبياً هو محاولة السيطرة على المرض والتخلص منه وهو المرحلة التي تلي عملية تشخيص المرض.[1][2][3] الهدف الرئيسي ...

Hutan AtlantikMata AtlânticaSebagian Hutan Atlantik di Serra do MarPetaPeta kawasan ekologi Hutan Atlantik seperti yang digambarkan oleh WWF. Garis kuning kurang lebih menanadakan tepian sebaran hutan(Citra satelit dari NASA)GeografiLokasiArgentina, Brasil, ParaguayArea1.315.460 km2 (507.900 sq mi)Hutan Atlantik (Portugis: Mata Atlântica) adalah sebuah hutan di Amerika Selatan yang membentang di sepanjang pesisir Atlantik Brasil dari Rio Grande do Norte di timur laut samp...

尼维涅和叙朗Nivigne et Suran 法國市镇尼维涅和叙朗的位置 尼维涅和叙朗显示法国的地图尼维涅和叙朗显示安省的地图坐标:46°15′51″N 5°25′39″E / 46.2641°N 5.4275°E / 46.2641; 5.4275国家 法國大区 奥弗涅-罗讷-阿尔卑斯大区省 安省区布雷斯地区布尔格区政府 • 市长 Bernard Prin(維基數據所列:Q65597191)面积1 • 市镇30.98 平方公...

関西テレビ放送 > 関西テレビソフトウェア 関西テレビソフトウェア株式会社KTV Softwares Inc.種類 株式会社市場情報 非上場略称 KTVS本社所在地 日本〒530-0056大阪府大阪市北区兎我野町7-11KTVエイトビル設立 1990年12月17日業種 情報・通信業法人番号 1120001062605 事業内容 コンピュータシステムの開発・販売・コンサルティング・運用・保守および、コンテンツ制作・字幕�...

1513 painting by Palma Vecchio Assumption of the VirginItalian: Assunzione della VergineArtistPalma VecchioYearc. 1513MediumOil on panelDimensions191 cm × 137 cm (75 in × 54 in)LocationGallerie dell'Accademia, Venice The Assumption of the Virgin is an oil on panel painting by Palma Vecchio, created c. 1513, now in the Gallerie dell'Accademia in Venice.[1][2] It shows an episode recounted in the apocryphal gospels - the Virgin M...

هذه المقالة عن فبراير أو شباط في الشهور السريانية. لالتقويم العبري، طالع شباط (عبري). فبرايرمعلومات عامةصنف فرعي من شهر في التقويم الميلادي(الجريجوري) جزء من تقويم يوليانيتقويم ميلاديالتقويم السويدي الاسم القائمة ... февраля (بالروسية) lutego (بالبولندية) лютага (بال�...

French lawyer and statesman (1859–1943) Millerand redirects here. Not to be confused with Mitterrand (disambiguation) or Millerand Island. Alexandre MillerandMillerand in 192012th President of FranceIn office23 September 1920 – 11 June 1924Prime MinisterGeorges LeyguesAristide BriandRaymond PoincaréFrédéric François-MarsalPreceded byPaul DeschanelSucceeded byGaston DoumerguePrime Minister of FranceIn office20 January 1920 – 23 September 1920PresidentRaymond Poincar...



