Fonction de Bessel
|
Read other articles:

CajamarcaPemandangan Cajamarca BenderaLambang kebesaranNegara PeruRegionCajamarca RegionProvinceProvinsi CajamarcaDibentuk19 Dscember 1802Pemerintahan • MayorVíctor Andrés Villar Narro (2019-2022) Ketinggian2.750 m (9,020 ft)Populasi • Total216 757 • Kepadatan metropolitan40,79/km2 (10,560/sq mi)Zona waktuUTC-5 (PET) • Musim panas (DST)UTC-5 (PET)Kode area telepon76Situs webhttp://www.cajamarcaperu.com/ http://www.muni...

Pius NjawéPius Njawé saat konferensi di ParisLahir4 Maret 1957Babouantou, KamerunMeninggal12 Juli 2010(2010-07-12) (umur 53)Chesapeake, Virginia, ASKebangsaanKamerunPekerjaanjurnalisOrganisasiLe MessagerSuami/istriJane NjawéAnakdelapanPenghargaanCPJ International Press Freedom Award (1991)Golden Pen of Freedom Award(1993)World Press Freedom Hero (2000) Pius Njawé (4 Maret 1957 – 12 Juli 2010) seorang jurnalis dan direktur Le Messager serta Le Messager Populi. Ditangk...

James Mark Baldwin tahun 1917 James Mark Baldwin (12 Januari 1861, Columbia, South Carolina – 8 November 1934, Paris)[1][2] adalah filsuf dan psikolog Amerika Serikat. Ia menamatkan pendidikannya di Universitas Princeton, dan juga merupakan salah satu pendiri Departemen Psikologi di universitas tersebut. Selain itu, Baldwin telah banyak menyumbang untuk bidang psikologi, psikiatri, dan evolusi. Contohnya, efek Baldwin yang dinamai darinya mengusulkan mekanisme seleksi kemamp...

QinnasrinArab: قنسرينcode: ar is deprecated Lokasi di SyriaLokasiSyriaWilayahKegubernuran AleppoKoordinat35°59′55″N 36°59′53″E / 35.998611°N 36.998056°E / 35.998611; 36.998056 Qinnasrin ( قنسرين; bahasa Suryani: ܩܢܫܪܝܢ, Qinnašrīn; yang berarti Sarang Elang),[1] juga dikenal dengan berbagai romanisasi[n 1] dan awalnya dikenal sebagai Chalcis-on-Belus (bahasa Latin: Chalcis ad Belum;[2] Yunani: Χαλκὶς...

العلاقات العراقية - الفلسطينية العراق فلسطين السفارات سفارة دولة فلسطين لدى العراق السفير : أحمد عقل[1] العنوان : بغداد، العامرية، ش. السفارات. سفارة العراق لدى الأردن/تمثيل غير مقيم الحدود لا حدود برية بين البلدين رئيس وزراء العراق محمد �...

Drinking establishment catering to lesbians The Lexington Club (1997–2015), a.k.a. The Lex, was San Francisco's last remaining lesbian bar Part of a series onLGBT topics LesbianGayBisexualTransgender Sexual orientation and gender Aromanticism Asexuality Gray asexuality Biology Bisexuality Pansexuality Demographics Environment Gender fluidity Gender identity Gender role Gender variance Homosexuality Intersex Non-heterosexual Non-binary gender Queer Queer h...

American filmsby year 1890s 1890–1899 1900s 1900 1901 1902 1903 19041905 1906 1907 1908 1909 1910s 1910 1911 1912 1913 19141915 1916 1917 1918 1919 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 1934 1935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981...

51st season in existence of Paris Saint-Germainقالب:SHORTDESC:51st season in existence of Paris Saint-Germain باريس سان جيرمانموسم 2020–21الرئيسناصر الخليفيالمدربتوماس توخل(حتى 29 ديسمبر)ماوريسيو بوتشيتينو(ابتداء من 2 يناير)الملعببارك دي برينسالدوري الفرنسيالثانيكأس فرنساالفائزكأس الأبطال الفرنسيالفائزدوري أبطال أور...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

American sitcom television series (1977–1981) For the general category of show, see Soap opera. SoapGenreSitcomCreated bySusan Harris[1]Starring Rae Allen Jimmy Baio Rebecca Balding Roscoe Lee Browne John Byner Diana Canova Billy Crystal Cathryn Damon Nancy Dolman Michael Durrell Robert Guillaume Katherine Helmond Howard Hesseman Jay Johnson Gordon Jump Charles Lane Richard Libertini Robert Mandan Dinah Manoff Caroline McWilliams Allan Miller Lynne Moody Richard Mulligan Marla Penni...

Capital of the Northern Cape, South Africa City in Northern Cape, South AfricaKimberleyCityTop: City centre seen over the Big Hole, Middle left: Griqualand West High Court, right: Kimberley Town Hall, bottom left: Trinity Church, Honoured Dead Memorial, World War I MemorialKimberleyShow map of Northern CapeKimberleyShow map of South AfricaKimberleyShow map of AfricaCoordinates: 28°44′18″S 24°45′50″E / 28.73833°S 24.76389°E / -28.73833; 24.76389Country ...
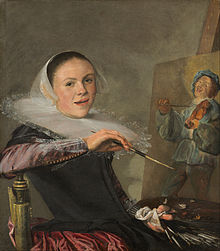
1631 painting by Judith Leyster The PropositionArtistJudith LeysterYear1631MediumOil on panelDimensions31 cm × 24 cm (11 3/8[1] in × 9.5[1] in)LocationRoyal Picture Gallery, Mauritshuis[1], The Hague The Proposition is a genre painting of 1631 by Judith Leyster, now in the Mauritshuis in The Hague, who title it Man offering money to a young woman.[2][3] It depicts a woman, sewing by candlelight, as a man leans...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Mountain in Malaysia Mount SilamHighest pointElevation884 m (2,900 ft)Prominence656 m (2,152 ft)Coordinates4°57′25″N 118°09′54″E / 4.957°N 118.165°E / 4.957; 118.165NamingNative nameGunung Silam (Malay)GeographyMount SilamLahad Datu District, Sabah, Malaysia Mount Silam (Malay: Gunung Silam) is a mountain in Lahad Datu District, Sabah, Malaysia. Description Mount Silam is 884 metres (2,900 ft) high and overlooks Darvel Bay...

This article is about parental warnings for black children. For parental sex education known as the talk, see The birds and the bees. Parenting issue in the United States Part of a series onDiscrimination Forms Institutional Structural Statistical Taste-based Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / Ethnicity Skin color Scientific racism Rank Sex Sexual orientation Species Size Viewpoint Social Arophobia Acephobi...

Портал:Политика Кыргызстан Статья из серии Политическая системаКыргызстана Конституция Президент Садыр Жапаров Кабинет министров Председатель кабинета министров Акылбек Жапаров Парламент Нурланбек Шакиев Судебная система Кыргызстана Верховный суд Конституционны�...

Убийство в Неммерсдорфе Место Маяковское Координаты 54°31′12″ с. ш. 22°03′56″ в. д.HGЯO Дата 21 октября 1944 Медиафайлы на Викискладе Тела немецких жителей, Неммерсдорф (указана дата снимка 20 октября 1944 года). Убийство в Не́ммерсдо́рфе (нем. Massaker von Nemmersdorf) — собы...

Political party in United States Moderate Party of Rhode Island ChairmanWilliam GilbertFounderKen BlockFounded2007; 17 years ago (2007)HeadquartersProvidence, Rhode Island, U.S.IdeologyCentrismFiscal conservatismPolitical positionCenterColors Blue, RedWebsiterimoderateparty.orgPolitics of United StatesPolitical partiesElections The Moderate Party of Rhode Island is the third-largest contemporary political party in the U.S. state of Rhode Island, after t...

Gereja Santo KristoforusGereja Santo Kristoforus, Paroki GrogolGereja Santo Kristoforus, GrogolLokasiJelambar, Grogol Petamburan, Jakarta Barat, JakartaNegaraIndonesiaDenominasiGereja Katolik RomaArsitekturStatusGereja parokiStatus fungsionalAktifAdministrasiParokiGrogolDekenatBarat IIKeuskupan AgungJakartaProvinsiJakarta Gereja Santo Kristoforus, Paroki Grogol adalah sebuah gereja paroki Katolik yang terletak di Grogol Petamburan, Jakarta Barat, Jakarta. Gereja ini berada dalam naungan Keusk...

John Flamsteed Sir John Flamsteed FRS 19 Agustus 1646 – 31 Desember 1719 adalah astronom Inggris dan astronom kerajaan (Astronomer Royal) pertama. Dia mencatat dalam katalog lebih dari 3000 bintang.[1] Penghargaan Fellow of the Royal Society (1676) Kawah Flamsteed di Bulan mengambil namanya Asteroid (4987) Flamsteed juga mengambil namanya Banyak sekolah dan perguruan tinggi di Derbyshire mengambil nama Flamsteed. T Rujukan ^ Robert Chambers, Book of Days Pranala luar (...

























![{\displaystyle Y_{\alpha }(x)\approx {\begin{cases}\displaystyle {\frac {2}{\pi }}\left[\ln \left({\frac {x}{2}}\right)+\gamma \right]&{\text{si }}\alpha =0\\\displaystyle -{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\text{si }}\alpha >0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55a99a1c1554cab024430f99491dc8f90f2e9fc5)







