Anneau d'Ore
|
Read other articles:

Peta menunjukkan lokasi Buenavista Buenavista adalah munisipalitas yang terletak di provinsi Marinduque, Filipina. Pada tahun 2010, munisipalitas ini memiliki populasi sebesar 21.018 jiwa atau 4.404 rumah tangga. Pembagian wilayah Secara administratif Buenavista terbagi menjadi 15 barangay, yaitu: Bagacay Bagtingon Bicas Bicas Caigangan Daykitin Libas Malbog Sihi Timbo (Sanggulong) Tungib-Lipata Yook Sarana pendidikan Sarana pendidikan yang tersedia di wilayah ini antara lain: Marinduque Vict...

Koordinat: 62°00′32″N 6°46′12″W / 62.009°N 6.770°W / 62.009; -6.770 Gedung pemerintahan di Tinganes. Tinganes adalah lokasi bersejarah landsstýri atau pemerintah Kepulauan Faroe yang terletak di kota Tórshavn. Istilah Tinganes berarti titik parlemen dalam bahasa Faroe. Majelis Faroe berkumpul di tempat untuk semenjak masa Viking. Para pendatang Norwegia mendirikan Ting (parlemen) mereka di lokasi ini pada tahun 825. Tinganes merupakan salah satu tempat pe...

Anjing laut dengan pemancar di belakangnya Telemetri (sejenis dengan telematika) adalah sebuah teknologi yang memungkinkan pengukuran jarak jauh dan pelaporan informasi kepada perancang atau operator sistem. Kata telemetri berasal dari akar bahasa Yunani tele = jarak jauh, dan metron = pengukuran. Sistem yang membutuhkan instruksi atau data yang dikirim kepada mereka untuk mengoperasikan membutuhkan lawan dari telemetri, telekomando.[1][2][3] Penjelasan Telemetri meruj...

Bandar Udara Internasional Incheon인천국제공항IATA: ICNICAO: RKSIWMO: 47113InformasiJenisPublikPemilikKementerian Agraria, Infrastruktur, dan TransportasiPengelolaIncheon International Airport CorporationMelayaniDaerah Ibu Kota Nasional SeoulLokasiDistrik Jung, Incheon, Korea SelatanDibuka29 Maret 2001; 23 tahun lalu (2001-03-29)Maskapai penghubung Air Incheon Air Premia Air Seoul Asiana Airlines FedEx Express Jeju Air Jin Air Korean Air Polar Air Cargo T'way Air Ketinggian dp...
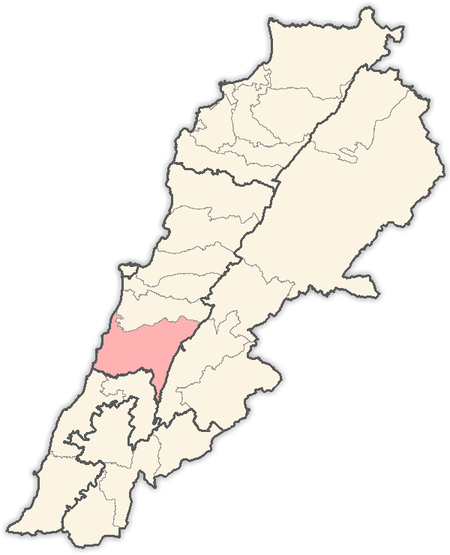
Municipality in Mount Lebanon, LebanonAmmatour عمّاطورMunicipalityAmmatourAmmatourLocation in Lebanon. The surrounding district can be seen on the map.Coordinates: 33°38′33″N 35°36′31″E / 33.64250°N 35.60861°E / 33.64250; 35.60861Country LebanonGovernorateMount LebanonDistrictChoufHighest elevation1,050 m (3,440 ft)Lowest elevation800 m (2,600 ft)Time zone+2 • Summer (DST)+3 Ammatour (Arabic: عمّاط�...

Ideology of the Chicano movement Chicanismo was based in the notion that Chicanos are native rather than immigrants by the situating of Aztlán in the southwestern US.[1] Part of a series onChicanos and Mexican Americans Terms Identity Chola/o La Raza Pachuca Pachuco Pinta/o Xicanx Concepts Anti-Mexican sentiment History Early-American Period Josefa Segovia Las Gorras Blancas Mexican–American War Mutualista San Elizario Salt War Sonoratown Treaty of Guadalupe Hidalgo Pre-Chicano Mov...

Constituency of the National Assembly of Pakistan NA-205 Naushahro Feroze-IConstituencyfor the National Assembly of PakistanRegionMehrabpur Tehsil, Bhiria Tehsil (partly) and Kandiaro Tehsil (partly) including Kandiaro town of Naushahro Feroze DistrictElectorate477,319 [1]Current constituencyMember(s)VacantCreated fromNA-212 Naushahro Feroze-II NA-205 Naushahro Feroze-I (این اے-205، نوشہروفِيروز-1) is a constituency for the National Assembly of Pakistan.[2] E...

1945–1948 US occupation of Korea Operation Blacklist FortyPart of the aftermath of World War II and the Cold WarLocationKorean PeninsulaObjectiveOccupation of Korea south of the 38th parallelDate1945–1948Executed by United StatesOutcomeSuccessful operation End of the Japanese rule of Korea Establishment of the United States Military Government Forceful dissolution of the People's Republic of Korea Establishment of the Republic of Korea Operation Blacklist Forty[1] was th...

Family of mammals belonging to even-toed ungulates This article is about the deer. For the French commune, see Chevrotaine. Not to be confused with Chevrotin. Kancil redirects here. For the car, see Perodua Kancil. ChevrotainTemporal range: late Eocene–Recent PreꞒ Ꞓ O S D C P T J K Pg N Tragulus kanchil Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Artiodactyla Suborder: Ruminantia Infraorder: Tragulina Family: TragulidaeH. Milne-E...

American author Lisa HallidayLisa at the Frankfurt Book Fair (2018)Born (1976-07-12) July 12, 1976 (age 47)Medfield, Massachusetts, U.S.Alma materHarvard UniversityOccupationAuthorYears active1997-presentNotable workAsymmetrySpouse Theo (m. 2009)Children1AwardsWhiting Award Lisa Halliday (born July 12, 1976) is an American author and novelist. She is most known for her novel Asymmetry, for which she received a Whiting Award in 2017.[1][...

Fibrocartilaginous part of a bone joint For other uses, see Meniscus (disambiguation). MeniscusHead of right tibia seen from above, showing menisci and attachments of ligamentsLeft knee-joint from behind, showing interior ligamentsDetailsIdentifiersLatinmeniscusGreekμηνίσκος (meniskos)MeSHD000072600TA98A03.0.00.033TA21544Anatomical terminology[edit on Wikidata] A meniscus (pl.: menisci or meniscuses) is a crescent-shaped fibrocartilaginous anatomical structure that, in contrast to...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Ministry-level body of the Taiwanese government Not to be confused with World Council of Indigenous Peoples. Council of Indigenous Peoples原住民族委員會Yuánzhù Mínzú Wěiyuánhuì (Mandarin)Ngièn-chhu-mìn-chhu̍k Vî-yèn-fi (Hakka)Agency overviewFormed10 December 1996 (as Council of Aboriginal Affairs)25 March 2002 (as Council of Indigenous Peoples)JurisdictionRepublic of China (Taiwan)HeadquartersNorth Tower, Xinzhuang Joint Office Tower, New TaipeiMinisters responsibleIcyang P...

For other uses, see Simplex (disambiguation). Multi-dimensional generalization of triangle The four simplexes that can be fully represented in 3D space. In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example, a 0-dimensional simplex is a point, a 1-dimensional simplex is a line segment, a 2-dim...

Species of black bass Largemouth redirects here. For the African cichlid, see Serranochromis. Largemouth bass Conservation status Least Concern (IUCN 3.1)[1] Secure (NatureServe)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Perciformes Family: Centrarchidae Genus: Micropterus Species: M. nigricans Binomial name Micropterus nigricans(Cuvier, 1828) Synonyms[3] Labrus salmoides Lacepède, 1...

Lihat entri libertas di kamus bebas Wiktionary. Patung LibertyLetakPulau LibertyManhattan, Kota New York,New York,[1] Amerika SerikatKetinggian Dari dasar patung hingga puncak: 151 kaki 1 inci (46 meter) Dari tanah hingga puncak: 305 kaki 1 inci (93 meter) Diresmikan28 Oktober 1886Dipugar1938, 1984–1986, 2011–2012PemahatFrédéric Auguste BartholdiPengunjung3,2 juta (tahun 2009)[2]Badan pengelolaNational Park Service Situs Warisan Dunia UNESCOJeni...

海洋性氣候 温带海洋性气候(英文:Temperate marine climate)是一种全年温和潮湿的气候类型,其特征十分明显:全年温和湿润。冬无严寒,夏无酷暑,全年降水分配较为均匀,但是冬天雨量較夏季多。分布在纬度40-60°之间的大陆西岸。 分布 位于南北纬40至60度的大陆西岸,除亚洲、非洲和南极洲没有外,其余各大洲都有,其中以歐洲大陸西部及不列顛群島最为典型�...

Sous-pages 27 28 29 30 31 ↑mars / avril↓ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 ↑avril / mai↓ 1 2 3 4 5 6 7 19 avril 2023 Ne mordez pas non plus les anciens. Quant aux chats, n'en parlons pas . Le (en) Concours de l'Image de l'année 2022 est ouvert sur WM Commons depuis deux jours (fin de ce 1er tour le 1er mai).Condition de vote : avoir fait au moins 75 editions avant le 1/1/2023 sur un projet WM et voter sur Commons sous un même compte (...

Nanosatellite ArgoMoonPrelaunch processing of ArgoMoon spacecraftOperatorASI / NASACOSPAR ID2022-156G SATCAT no.55907Mission duration634 days Spacecraft propertiesSpacecraftArgoMoonSpacecraft typeCubeSatBus6U CubeSatManufacturerArgotecPayload mass14 kg (31 lb)Dimensions12 cm x 24 cm x 36 cmPowerwatts Start of missionLaunch date16 November 2022, 06:47:44 UTC[1]RocketSLS Block 1Launch siteKSC, LC-39BContractorNASA Orbital parametersReference systemHeliocentric orbit ...





























