Ordre (théorie des anneaux)
|
Read other articles:

No, Thank YouPoster promosiHangul며느라기 GenreDramaBerdasarkanMyeoneuragioleh Soo Shin-jiPengembangKakao MSkenarioLee Yoo-jungSutradaraLee Kwang-youngPemeranPark Ha-sunKwon YulMoon Hee-kyungJmlh. episode12ProduksiProduser eksekutifMoon Sung-hoLee Young-seokDurasi19–25 menitRumah produksiSBS MobidicTake 2 Media GroupDistributorKakao MRilis asliJaringanKakaoTVRilis21 November 2020 (2020-11-21) –6 Februari 2021 (2021-2-6) No, Thank You (Hangul: 며느라기;...

Administrative entry restrictions Algerian biometric passport Visa requirements for Algerian citizens are administrative entry restrictions by the authorities of other states placed on citizens of Algeria. As of march 2024 , Algerian citizens had visa-free or visa on arrival access to 60 countries and territories and have the eligible to an e-visa for 38 countries, ranking the Algerian passport 86th in terms of travel freedom (tied with the passport of Jordan) according to the Henley Passport...

American politician A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (January 2023) (Learn how and when to remove this template message) Tom DiNapoli54th Comptroller of New YorkIncumbentAssumed office February 7, 2007GovernorEliot SpitzerDavid PatersonAndrew CuomoKathy HochulPreceded byThomas Sanzillo (Acti...

Tentara PBB, bagian dari Misi PBB di Ethiopia dan Eritrea, sedang mengawasi perbatasan Eritrea-Ethiopia. Pemeliharaan perdamaian atau penjagaan perdamaian mengacu pada aktivitas yang bertujuan menciptakan kondisi yang memungkinkan perdamaian jangka panjang.[1] Dalam perkumpulan pemerintahan dan organisasi Perserikatan Bangsa-Bangsa, ada keyakinan umum bahwa di tingkat internasional, pemelihara perdamaian mengawasi proses perdamaian di wilayah-wilayah pascakonflik dan membantu mantan k...

Newcastle United 2000–01 football seasonNewcastle United2000–01 seasonChairmanFreddy ShepherdManagerSir Bobby RobsonStadiumSt. James' ParkPremier League11thFA CupThird roundLeague CupFourth roundTop goalscorerLeague: Cort/Solano (6)All: Cort/Solano/Shearer (7)Average home league attendance51,309 Home colours Away colours ← 1999–20002001–02 → During the 2000–01 English football season, Newcastle United F.C. competed in the FA Premier League. This article covers...

Group of Carmelites executed during the French Revolution in Compiègne, France (1794) This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Martyrs of Compiègne – news ...

Martin Ziguélé Perdana Menteri Republik Afrika TengahMasa jabatan1 April 2001 – 15 Maret 2003PendahuluAnicet-Georges DologuéléPenggantiAbel Goumba Informasi pribadiLahir12 Februari 1957 (umur 67)Sunting kotak info • L • B Martin Ziguélé (lahir 12 Februari 1957[1]) ialah seorang politikus Republik Afrika Tengah yang menjadi Perdana Menteri Republik Afrika Tengah dari tahun 2001 hingga 2003. Ia menduduki urutan ke-2 dalam PilPres 2005 dan kini menjadi...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2023) ديراجنيا ديراجنيا تقسيم إداري البلد أوكرانيا [1] التقسيم الأعلى خ...

American baseball umpire (born 1981) Baseball player David RackleyRackley as a Minor League umpire, 2006Born: (1981-10-11) October 11, 1981 (age 42)Houston, Texas, U.S.MLB debutAugust 13, 2010 Crew InformationUmpiring crew3Crew members#27 Larry Vanover (crew chief)#87 Scott Barry#86 David Rackley#96 Chris Segal Career highlights and awardsSpecial assignments All-Star Games (2021) Wild Card Games/Series (2016, 2017, 2019, 2020) Division Series (2020, 2022, 2023) League Championship Series...

Species of tree (walnut) Juglans regia Mature walnut tree Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Fagales Family: Juglandaceae Genus: Juglans Section: Juglans sect. Juglans Species: J. regia Binomial name Juglans regiaL. Distribution map Synonyms[citation needed] J. duclouxiana DodeJ. fallax DodeJ. kamaonica (C. de Candolle) DodeJ. orientis...

Cattedrale imperiale di Santa MariaMarienkaiserdomEsternoStato Germania LandRenania Settentrionale-Vestfalia LocalitàAquisgrana Coordinate50°46′29″N 6°05′04″E50°46′29″N, 6°05′04″E Religionecattolica di rito romano TitolareSanta Maria Assunta Diocesi Aquisgrana ArchitettoOddone da Metz Stile architettonicobizantino, gotico, barocco Inizio costruzione786 CompletamentoXVIII secolo Sito webwww.aachenerdom.de/, www.aachenerdom.de/en/ e www.aachenerdom.de/fr/ Modifica dati...

Military rank for a senior non-commissioned officer in the armed forces of some countries This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Senior master sergeant – news · newspapers · books · scholar · JSTOR (January 2022) (Learn how and when to remove this message) Senior master sergeant is the military rank...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2017) تقييم الأثر الاجتماعي (بالإنجليزية: Social impact assessment) وتُعرف اختصاراً بـ SIA، هي منهجية تهدف إلى التنبؤ وقياس الآثار المترتبة عن السياسات العمومية أو الخاصة، أ�...

Elizabeth Okie PaxtonLahirElizabeth Vaughan Okie(1878-03-17)17 Maret 1878Providence, Rhode IslandMeninggal2 April 1972(1972-04-02) (umur 94)Boston, MassachusettsKebangsaanAmerikaPendidikanCowles Art SchoolDikenal atasModern still life and interior paintingsKarya terkenalThe Breakfast TrayGerakan politikBoston SchoolSuami/istriWilliam McGregor Paxton Elizabeth Okie Paxton (17 Maret 1878 – 2 April 1972[nb 1] adalah seorang pelukis Amerika, menikah dengan seniman la...

سانتا ماريا دي لوس يانوس (بالإسبانية: Santa María de los Llanos)[1] - بلدية - سانتا ماريا دي لوس يانوس سانتا ماريا دي لوس يانوس تقسيم إداري البلد إسبانيا [2] المقاطعة قونكة خصائص جغرافية إحداثيات 39°29′24″N 2°48′30″W / 39.49°N 2.8083333333333°W / 39.49; -2.80833...

Canadian honours system The orders, decorations, and medals of Canada comprise a complex system by which Canadians are honoured by the country's sovereign for actions or deeds that benefit their community or the country at large. Modelled on its British predecessor, the structure originated in the 1930s, but began to come to full fruition at the time of Canada's centennial in 1967, with the establishment of the Order of Canada, and has since grown in both size and scope to include dynastic an...

Championnat du monde senior de curling 2016 Généralités Sport Curling Organisateur(s) Fédération mondiale de curling Édition 15e édition Lieu(x) Karlstad (Suède) Date du 16 au 23 avril 2016 Participants 27 nations 17 nations Palmarès Vainqueur Suède Écosse Deuxième Canada Allemagne Troisième Irlande Suède Navigation Édition précédente Édition suivante modifier Le Championnat du monde senior de curling 2016 (nom officiel : World Senior Curling Championships) ...

Castillo de Santa Catalina oAlcázar Nuevo Bien de interés cultural Alcázar Nuevo en el Castillo de JaénUbicaciónPaís EspañaComunidad Andalucía AndalucíaProvincia Jaén JaénLocalidad JaénUbicación MontañaCoordenadas 37°46′03″N 3°47′58″O / 37.76745, -3.79948CaracterísticasTipo CastilloConstrucción Siglos XIII y XIVAltura 30 mPropietario Ayuntamiento de JaénEntrada Sí Bien de interés culturalPatrimonio histórico de EspañaCategoría Mo...
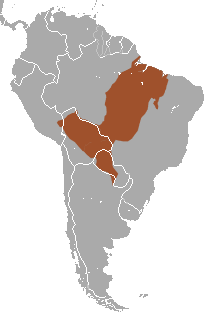
Species of New World monkey Azara's night monkey[1] Azara's night monkey (A. a. infulatus) at Cristalino Jungle Lodge, Mato Grosso, Brazil Conservation status Least Concern (IUCN 3.1)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Primates Suborder: Haplorhini Infraorder: Simiiformes Family: Aotidae Genus: Aotus Species: A. azarae Binomial name Aotus azarae(Humboldt, 1811) Azara's night monkey range Azara's n...

1980 book by Gilles Deleuze and Félix Guattari Mille Plateaux redirects here. For the record label, see Mille Plateaux (record label). A Thousand Plateaus Cover of the first editionAuthorsGilles DeleuzeFélix GuattariOriginal titleMille plateauxTranslatorBrian MassumiLanguageFrenchSeriesCapitalism and SchizophreniaSubjectPhilosophyschizoanalysismicropoliticsaestheticspolitical economyPublished 1980 (Les Éditions de Minuit, in French) 1987 (University of Minnesota Press, in English) Pub...