Morphisme d'anneaux
|
Read other articles:

Dara biru Mauritius Alectroenas nitidissimus Status konservasiPunahIUCN22691601 TaksonomiKerajaanAnimaliaFilumChordataKelasAvesOrdoColumbiformesFamiliColumbidaeGenusAlectroenasSpesiesAlectroenas nitidissimus Scopoli, 1786 Tata namaSinonim takson List Columba nitidissima Scopoli, 1786 Columba franciae Gmelin, 1789 Columba batavica Bonnaterre, 1790 Columba jubata Wagler, 1827 Alectroenas franciae Gray, 1840 Alectroenas nitidissimus Columbigallus franciae Des Murs, 1854 Ptilopus nitidissimus Sch...

Craig Moore Moore bermain untuk Queensland RoarInformasi pribadiNama lengkap Craig Andrew MooreTanggal lahir 12 Desember 1975 (umur 48)Tempat lahir Sydney, AustraliaTinggi 185 m (606 ft 11 in)Posisi bermain BekKarier junior1991 North Star1992–1993 AISKarier senior*Tahun Tim Tampil (Gol)1994–1998 Rangers 73 (4)1998–1999 Crystal Palace 23 (3)1999–2005 Rangers 102 (10)2005 Borussia Mönchengladbach 13 (1)2005–2007 Newcastle United 31 (0)2007–2009 Brisbane Roar 62...

FiveAlbum studio karya SHINeeDirilis27 Januari 2017 (2017-01-27) (Digital)22 Februari 2017 (2017-02-22) (Fisik)Direkam2016–17Genre Pop pop rock teen pop BahasaJepangLabelEMI Records Japan (EMI Records)ProduserLee Soo Man (eksekutif)Kronologi SHINee 1 of 1(2016)1 of 12016 Five(2017) Shinee The Best From Now On(2018)Shinee The Best From Now On2018 Singel dalam album Five Kimi no SeideDirilis: 18 Mei 2016 Winter WonderlandDirilis: 21 Desember 2016 Get the TreasureDirilis: 27 Janu...
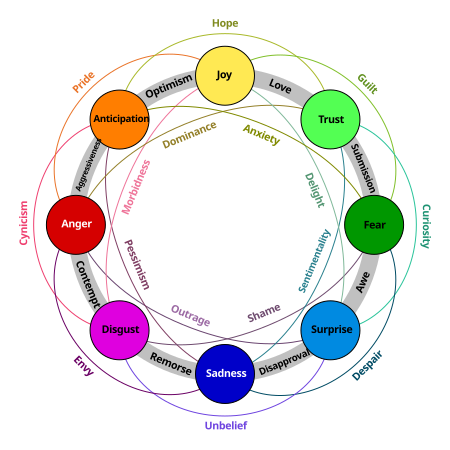
Activities to build emotional intelligence This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Emotional thought method – news · newspapers · books · scholar · JSTOR (November 2019) (Learn how and when to remove this template message) This article may require copy editing for grammar, style, cohesion, tone, or s...

Pour un article plus général, voir Élections municipales de 2020 dans le Loiret. 2014 2026 Élections municipales de 2020 à Orléans 15 mars et 28 juin 2020 Type d’élection Élections municipales Postes à élire 55 sièges au conseil municipal Corps électoral et résultats Population 116 685 Inscrits 62 896 Votants au 1er tour 22 635 35,99 % 17,9 Votes exprimés au 1er tour 22 143 Votes blancs au 1er tour 166 Votes nuls au 1er tour 326 Vo...

User-driven research site (2006-2013) AskvilleType of siteCollaborationAvailable inEnglishOwnerAmazon.comURLhttp://askville.amazon.comCommercialyesRegistrationRequiredLaunchedDecember 8, 2006; 17 years ago (2006-12-08)Current statusInactive as of October 25, 2013 Askville was a user-driven research site founded by Amazon.com. It was opened to the public on December 8, 2006, and shut down on October 25, 2013. History Askville was co-founded by Korean-American former...

Science award This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely...

Former American trucking and logistics company Consolidated FreightwaysFormerlyConsolidated Truck LinesCompany typePublicIndustryTransportationDistributionFoundedApril 1, 1929; 95 years ago (1929-04-01) in Portland, OregonFounderLeland JamesDefunctSeptember 2002 (2002-09)FateChapter 11 bankruptcySuccessorCon-wayNumber of locationsPortland, OregonVancouver, WashingtonServicesLTL shippingLogistics Consolidated Freightways (CF) was an American multinational less-than-...

Non-profit scientific and educational society This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: National Council for Geographic Education – news · newspapers · books · scholar · JSTOR (September 2016) (L...

اقتصاد روسياMIBC ، أحد أكبر المراكز المالية في أوروباعامالدولة روسياعملة روبل روسي (RUB, ₽)السنة المالية تقويم سنوي[1]المنظمات WTO، بريكس، منتدى الدول المصدرة للغاز، CIS، APEC، EAEU، G-20 and othersالإحصائياتالناتج الإجمالي ▼ $1.4 trillion (nominal, 2020 est.)[10] ▼ $4.0 trillion (PPP, 2020 est.)[10] نمو ال�...

Coach Wooden Keys to Life AwardAwarded forQualities exemplified by Coach Wooden: outstanding character, integrity, and leadership on the court, in the work place, in the home, and in the communityCountryUnited StatesPresented byAthletes in ActionHistoryFirst award1998Most recentBilly Kennedy, Texas A&M and his wife Mary KennedyWebsitelegendsbreakfast.net The Coach Wooden Keys to Life Award is presented annually to a member of the college or professional basketball community who lives out...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sulaimankhel – news · newspapers · books · scholar · JSTOR (January 2015) (Learn how and when to remove thi...

Ayub Akbar Direktur Umum Pusat Teritorial Angkatan DaratPetahanaMulai menjabat 1 April 2024PendahuluRikas HidayatullahPenggantiPetahanaDanrem 143/Halu OleoMasa jabatan29 Maret 2023 – 1 April 2024PendahuluYufti SenjayaPenggantiRaden Wahyu SugiartoKomandan Resimen Induk Kodam JayakartaMasa jabatan2021–2023PendahuluPrasetyoPenggantiSuwondo Informasi pribadiLahir3 November 1970 (umur 53)Padang, Sumatera BaratAlma materAkademi Militer (1995)Karier militerPihak IndonesiaD...

Empress of Russia from 1825 to 1855 Charlotte of Prussia redirects here. For the daughter of Frederick III, German Emperor, see Princess Charlotte of Prussia. For the first wife of George II, Duke of Saxe-Meiningen, see Princess Charlotte of Prussia (1831–1855). Alexandra FeodorovnaPortrait by Franz Krüger, c. 1836Empress consort of RussiaTenure1 December 1825 – 2 March 1855Coronation3 September 1826BornPrincess Charlotte of Prussia(1798-07-13)13 July 1798Charlottenburg Palace, Ber...

You can help expand this article with text translated from the corresponding article in Spanish. (October 2009) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wiki...

French journalist This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Victor Noir – news · newspapers · books · scholar · JSTOR (November 2019) (Learn how and when to remove this message) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to im...

Questa voce o sezione sull'argomento pallavolisti non è ancora formattata secondo gli standard. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Yunieska RoblesNazionalità Cuba Altezza185 cm Peso70 kg Pallavolo RuoloSchiacciatrice/Opposto Squadra Šygys Öskemen CarrieraSquadre di club ?-2012 Isla de la Juventud2012-2013 Lokomotiv Biləcəri2013-2014 Azərreyl2015 Al-Ahly2015- Šygys Ö...

Audition by the Beatles in London, 1962 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Beatles' Decca audition – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this message) History of the BeatlesThe Beatles logo The Quarrymen In Hamburg At the Cavern Club Decc...

Alice Guszalewicz as Salome in the Richard Strauss opera, c. 1910.[n 1] Salome by Oscar Wilde, a play written in 1891 and first produced in 1896, has been analysed by numerous literary critics, and has prompted numerous derivatives. The play depicts the events leading to the execution of Iokanaan (John the Baptist) at the instigation of Salome, step-daughter of Herod Antipas, and her death on Herod's orders. Themes Wilde's interest in Salomé's image had been stimulated by description...

Lithuanian priest and activist in Vilnius county This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Petras Kraujalis – news · newspapers · books · scholar · JSTOR (November 2020) (Learn how and when to remove this message) Petras KraujalisBorn(1882-07-08)8 July 1882Žagarai [lt], Russian EmpireDied...
