Signed area
|
Read other articles:

Bambi IISampul DVDSutradaraBrian PimentalProduserJim BallantineJeffrey MoznettDave OkeyDitulis olehAlicia KirkBen GluckPemeranAlexander GouldPatrick StewartBrendon BaergNicky JonesAndrea BowenAnthony GhannamKeith FergusonEli LinnetzBrian PimentalCarolyn HennesyCree SummerAriel WinterMcKenna CowgillEmma Rose LinaDistributorWalt Disney PicturesBuena Vista Home EntertainmentTanggal rilis26 Januari 2006 (Argentina)7 Februari 2006 (A.S.)24 April 2006 (A.S.)26 Mei 2006 (Australia)Durasi72 menit (AS...

Audacious Audacious 4.1Tipeaudio player software (en) BerdasarkaBeep Media Player (en) Versi pertama24 Oktober 2005Versi stabil 4.3.1 (29 April 2023) GenrePemutar mediaLisensilisensi BSDBahasaDaftar bahasa Multiple languages Karakteristik teknisSistem operasiMirip Unix, Windows XP dan versi yang lebih baruBahasa pemrogramanC++ dan C Format berkasDaftarPortable Sound Format (en) Antarmuka BibliotecaGTK dan Qt Sumber kode Kode sumberPranala Debianaudacious Arch Linuxaudacious Ubuntuaudacious Ge...

Halaman ini berisi artikel tentang pasal 6 Kitab Bilangan dalam Alkitab Kristen atau Ibrani. Untuk bilangan dalam arti angka 6, lihat 6 (angka). Bilangan 6Kitab Bilangan lengkap pada Kodeks Leningrad, dibuat tahun 1008.KitabKitab BilanganKategoriTauratBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen4← pasal 5 pasal 7 → Bilangan 6 (disingkat Bil 6) adalah pasal keenam Kitab Bilangan dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Termasuk dalam kumpulan k...

Череп с костями, распространённый символ для обозначения яда Символы опасности — графический элемент (пиктограмма), передающий в сжатом виде информацию для идентификации специфических рисков и необходимых мер предосторожности. В сочетании с другими графическими элем�...

Emanuela Rossi in E adesso sesso (2001) Emanuela Rossi (Roma, 24 gennaio 1959) è una doppiatrice, direttrice del doppiaggio, dialoghista e attrice italiana. Indice 1 Biografia 2 Vita privata 3 Filmografia 3.1 Cinema 3.2 Televisione 4 Doppiaggio 4.1 Film 4.2 Film d'animazione 4.3 Serie televisive e miniserie 4.4 Soap opera e telenovelas 4.5 Cartoni animati 4.6 Radio 4.7 Videogiochi 5 Radio 6 Note 7 Altri progetti 8 Collegamenti esterni Biografia Emanuela Rossi nel 1984 Attiva come interprete ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Pan Am Flight 1-10 – news · newspapers · books · scholar · JSTOR (January 2023) (Learn how and when to remove this template message) 1948 aviation accident Pan Am Flight 1-10Pan Am Lockheed L-049 Constellation Clipper Great Republic at London Heathrow, similar ...

4BeBeriliumSampel berilium Garis spektrum beriliumSifat umumNama, lambangberilium, BePengucapan/bèrilium/[1] Penampilanmetalik putih abu-abuBerilium dalam tabel periodik 4Be Hidrogen Helium Lithium Berilium Boron Karbon Nitrogen Oksigen Fluor Neon Natrium Magnesium Aluminium Silikon Fosfor Sulfur Clor Argon Potasium Kalsium Skandium Titanium Vanadium Chromium Mangan Besi Cobalt Nikel Tembaga Seng Gallium Germanium Arsen Selen Bromin Kripton Rubidium Strontium Yttrium Zirconium N...

For the asteroid named after Nikolaus Lenau, see 7400 Lenau. Austrian poet Lenau in 1839 Nikolaus Lenau was the pen name of Nikolaus Franz Niembsch Edler von Strehlenau (13 August 1802 – 22 August 1850), a German-language Austrian poet. Biography Lenau's Grave in Weidling, Austria He was born at Csatád (Schadat), Kingdom of Hungary, now Lenauheim, Banat, then part of the Habsburg monarchy, now in Romania. His father, a Habsburg government official, died in 1807 in Budapest, leaving his chi...

銮披汶·頌堪แปลก พิบูลสงคราม第3任泰國總理任期1938年12月16日—1944年8月1日君主國王拉玛八世前任披耶帕凤侯爵继任寬·阿派旺第8任泰國總理任期1948年4月8日—1957年9月16日君主國王拉玛九世前任寬·阿派旺继任乃朴·沙拉信 个人资料出生貝·基達桑卡(1897-07-14)1897年7月14日 暹罗暖武里府逝世1964年6月11日(1964歲—06—11)(66歲) 日本神奈川縣相模原市国籍&#...

Scottish sports commentator Derek RaeBorn (1967-04-09) 9 April 1967 (age 57)Aberdeen, ScotlandEducationAberdeen UniversityOccupationFootball commentatorEmployer(s)ESPN (United States)Deutsche Fußball Liga (Worldwide)Amazon Prime Video (United Kingdom) Derek Rae (born 9 April 1967[1]) is a Scottish association football commentator and presenter who currently works for ESPN and ABC in the United States for the English-language coverages of Bundesliga, DFB Pokal, and La Liga and De...

Questa voce o sezione sull'argomento Angola non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Luandamunicipalità(PT) Luanda Luanda – Veduta LocalizzazioneStato Angola ProvinciaLuanda TerritorioCoordinate8°49′51″S 13°14′42″E / 8.830833°S 13.245°E-8.830833; 13.245 (Luanda)Coordinate: 8°49′51″S 13°14′42″E...

1987 historical fantasy novel by Tim Powers This article is about the 1987 novel by Tim Powers. For the 2011 film, see Pirates of the Caribbean: On Stranger Tides. On Stranger Tides First edition cover.AuthorTim PowersCover artistJames GurneyCountryUnited StatesLanguageEnglishGenreHistorical fantasyPublisherAce Books (Hardcover edition)Publication dateNovember 1987Media typePrint (Hardback & Paperback)Pages325ISBN978-0-441-62683-0OCLC15661924 On Stranger Tides is a 1987 historic...

1877 Japanese samurai revolt Satsuma RebellionPart of the Shizoku rebellionsMap of the campaignDate29 January – 24 September 1877LocationKyūshū, JapanResult Imperial victoryBelligerents Empire of Japan Satsuma DomainCommanders and leaders Emperor Meiji Prince Arisugawa Yamagata Aritomo Kuroda Kiyotaka Tani Tateki Saigō Takamori † Kirino Toshiaki † Beppu Shinsuke † Strength 51,800 imperial army 5,054 imperial guardsmen 18,000 police 12,000 infantry 2...
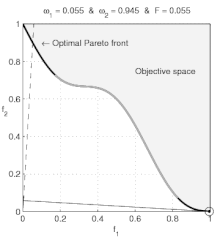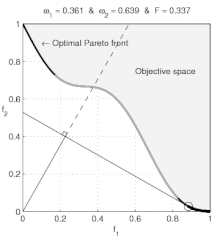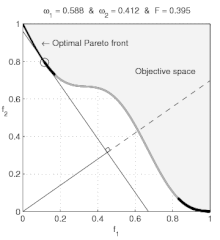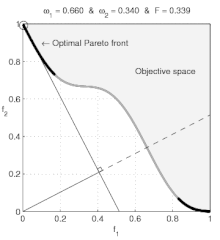
Violations of the convexity assumptions of elementary economics Non-convexity (economics) is included in the JEL classification codes as JEL: C65 In economics, non-convexity refers to violations of the convexity assumptions of elementary economics. Basic economics textbooks concentrate on consumers with convex preferences (that do not prefer extremes to in-between values) and convex budget sets and on producers with convex production sets; for convex models, the predicted economic behavi...

Military unit used by naval forces, usually comprising a number of ships For other uses, see Squadron (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Squadron naval – news · newspapers · books · scholar · JSTOR (August 2008) (Learn how and when to remove this message) Naval units and f...

British footballer (born 1971) This article is about the footballer. For the engineer, see David James Wetherall. For the medic, see David Weatherall. David WetherallPersonal informationFull name David Wetherall[1]Date of birth (1971-03-14) 14 March 1971 (age 53)[1]Place of birth Sheffield, EnglandHeight 6 ft 3 in (1.91 m)Position(s) DefenderSenior career*Years Team Apps (Gls)1989–1991 Sheffield Wednesday 0 (0)1991–1999 Leeds United 202 (12)1999–2008 ...

1987 studio album by Midnight OilDiesel and DustStudio album by Midnight OilReleased2 August 1987RecordedJanuary–April 1987StudioAlbert (Sydney)GenreAlternative rockLength46:37LabelSprint / ColumbiaProducerWarne Livesey, Midnight OilMidnight Oil chronology Species Deceases(1985) Diesel and Dust(1987) Blue Sky Mining(1990) Singles from Diesel and Dust The Dead HeartReleased: August 1986 Beds Are BurningReleased: August 1987 Put Down That WeaponReleased: December 1987 DreamworldRelea...

شادي رياض معلومات شخصية الميلاد 17 يونيو 2003 (العمر 21 سنة)ميورقة الطول 1.87 م (6 قدم 1 1⁄2 بوصة) مركز اللعب مدافع الجنسية المغرب معلومات النادي النادي الحالي ريال بيتيس(مُعاراً من برشلونة) الرقم 28 مسيرة الشباب سنوات فريق 2009–2011 Atlético Rafal 2011–2014 ريال مايوركا 2014–20...

Events at the2003 World ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen5000 mmenwomen10,000 mmenwomen100 m hurdleswomen110 m hurdlesmen400 m hurdlesmenwomen3000 msteeplechasemen4 × 100 m relaymenwomen4 × 400 m relaymenwomenRoad eventsMarathonmenwomen20 km walkmenwomen50 km walkmenField eventsHigh jumpmenwomenPole vaultmenwomenLong jumpmenwomenTriple jumpmenwomenShot putmenwomenDiscus throwmenwomenHammer throwmenwomenJavelin throwmenwomenCombined ...

Municipality in Quebec, CanadaSaint-ZénonMunicipalityLocation within Matawinie RCM.Saint-ZénonLocation in central Quebec.Coordinates: 46°33′N 73°49′W / 46.550°N 73.817°W / 46.550; -73.817[1]Country CanadaProvince QuebecRegionLanaudièreRCMMatawinieConstitutedOctober 7, 1895Named forZeno of Verona[1]Government[2] • MayorKarl Lacouvée • Federal ridingJoliette • Prov. ridingBerthierArea[...

































