Part of a series of articles about
Calculus
${\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)}$
Fundamental theorem Limits Continuity Rolle's theorem Mean value theorem Inverse function theorem
Differential Definitions Derivative (generalizations) Differential infinitesimal of a function total Concepts Differentiation notation Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem Rules and identities Sum Product Chain Power Quotient L'Hôpital's rule Inverse General Leibniz Faà di Bruno's formula Reynolds
Integral Lists of integrals Integral transform Leibniz integral rule Definitions Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration Integral of inverse functions Integration by Parts Discs Cylindrical shells Substitution (trigonometric, tangent half-angle, Euler) Euler's formula Partial fractions (Heaviside's method) Changing order Reduction formulae Differentiating under the integral sign Risch algorithm
Series Geometric (arithmetico-geometric) Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector Gradient Divergence Curl Laplacian Directional derivative Identities Theorems Gradient Green's Stokes' Divergence generalized Stokes Helmholtz decomposition
Multivariable Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian
Advanced Calculus on Euclidean space Generalized functions Limit of distributions
Specialized Fractional Malliavin Stochastic Variations
Miscellanea Precalculus History Glossary List of topics Integration Bee Mathematical analysis Nonstandard analysis
v t e

In calculus, Rolle's theorem or Rolle's lemma essentially states that any real-valued differentiable function that attains equal values at two distinct points must have at least one point, somewhere between them, at which the slope of the tangent line is zero. Such a point is known as a stationary point. It is a point at which the first derivative of the function is zero. The theorem is named after Michel Rolle.

If a real-valued function f is continuous on a proper closed interval [a, b], differentiable on the open interval (a, b), and f (a) = f (b), then there exists at least one c in the open interval (a, b) such that $${\displaystyle f'(c)=0.}$$

This version of Rolle's theorem is used to prove the mean value theorem, of which Rolle's theorem is indeed a special case. It is also the basis for the proof of Taylor's theorem.

Although the theorem is named after Michel Rolle, Rolle's 1691 proof covered only the case of polynomial functions. His proof did not use the methods of differential calculus, which at that point in his life he considered to be fallacious. The theorem was first proved by Cauchy in 1823 as a corollary of a proof of the mean value theorem.^[1] The name "Rolle's theorem" was first used by Moritz Wilhelm Drobisch of Germany in 1834 and by Giusto Bellavitis of Italy in 1846.^[2]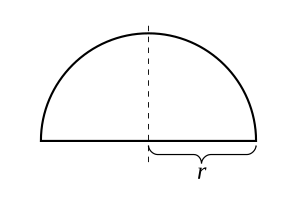

For a radius r > 0, consider the function $${\displaystyle f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].}$$

Its graph is the upper semicircle centered at the origin. This function is continuous on the closed interval [−r, r] and differentiable in the open interval (−r, r), but not differentiable at the endpoints −r and r. Since f (−r) = f (r), Rolle's theorem applies, and indeed, there is a point where the derivative of f is zero. The theorem applies even when the function cannot be differentiated at the endpoints because it only requires the function to be differentiable in the open interval.

If differentiability fails at an interior point of the interval, the conclusion of Rolle's theorem may not hold. Consider the absolute value function $${\displaystyle f(x)=|x|,\quad x\in [-1,1].}$$

Then f (−1) = f (1), but there is no c between −1 and 1 for which the f ′(c) is zero. This is because that function, although continuous, is not differentiable at x = 0. The derivative of f changes its sign at x = 0, but without attaining the value 0. The theorem cannot be applied to this function because it does not satisfy the condition that the function must be differentiable for every x in the open interval. However, when the differentiability requirement is dropped from Rolle's theorem, f will still have a critical number in the open interval (a, b), but it may not yield a horizontal tangent (as in the case of the absolute value represented in the graph).

Rolle's theorem implies that a differentiable function whose derivative is ⁠${\displaystyle 0}$⁠ in an interval is constant in this interval.

Indeed, if a and b are two points in an interval where a function f is differentiable, then the function $${\displaystyle g(x)=f(x)-f(a)-{\frac {f(b)-f(a)}{b-a}}(x-a)}$$ satisfies the hypotheses of Rolle's theorem on the interval ⁠${\displaystyle [a,b]}$⁠.

If the derivative of ⁠${\displaystyle f}$⁠ is zero everywhere, the derivative of ⁠${\displaystyle g}$⁠ is $${\displaystyle g'(x)={\frac {f(b)-f(a)}{b-a}},}$$ and Rolle's theorem implies that there is ⁠${\displaystyle c\in (a,b)}$⁠ such that $${\displaystyle 0=g'(x)={\frac {f(b)-f(a)}{b-a}}.}$$

Hence, ⁠${\displaystyle f(a)=f(b)}$⁠ for every ⁠${\displaystyle a}$⁠ and ⁠${\displaystyle b}$⁠, and the function ⁠${\displaystyle f}$⁠ is constant.

The second example illustrates the following generalization of Rolle's theorem:

Consider a real-valued, continuous function f on a closed interval [a, b] with f (a) = f (b). If for every x in the open interval (a, b) the right-hand limit $${\displaystyle f'(x^{+}):=\lim _{h\to 0^{+}}{\frac {f(x+h)-f(x)}{h}}}$$ and the left-hand limit $${\displaystyle f'(x^{-}):=\lim _{h\to 0^{-}}{\frac {f(x+h)-f(x)}{h}}}$$

exist in the extended real line [−∞, ∞], then there is some number c in the open interval (a, b) such that one of the two limits $${\displaystyle f'(c^{+})\quad {\text{and}}\quad f'(c^{-})}$$ is ≥ 0 and the other one is ≤ 0 (in the extended real line). If the right- and left-hand limits agree for every x, then they agree in particular for c, hence the derivative of f exists at c and is equal to zero.

• If f is convex or concave, then the right- and left-hand derivatives exist at every inner point, hence the above limits exist and are real numbers.
• This generalized version of the theorem is sufficient to prove convexity when the one-sided derivatives are monotonically increasing:^[3] $${\displaystyle f'(x^{-})\leq f'(x^{+})\leq f'(y^{-}),\quad x<y.}$$

Since the proof for the standard version of Rolle's theorem and the generalization are very similar, we prove the generalization.

The idea of the proof is to argue that if f (a) = f (b), then f must attain either a maximum or a minimum somewhere between a and b, say at c, and the function must change from increasing to decreasing (or the other way around) at c. In particular, if the derivative exists, it must be zero at c.

By assumption, f is continuous on [a, b], and by the extreme value theorem attains both its maximum and its minimum in [a, b]. If these are both attained at the endpoints of [a, b], then f is constant on [a, b] and so the derivative of f is zero at every point in (a, b).

Suppose then that the maximum is obtained at an interior point c of (a, b) (the argument for the minimum is very similar, just consider −f ). We shall examine the above right- and left-hand limits separately.

For a real h such that c + h is in [a, b], the value f (c + h) is smaller or equal to f (c) because f attains its maximum at c. Therefore, for every h > 0, $${\displaystyle {\frac {f(c+h)-f(c)}{h}}\leq 0,}$$ hence $${\displaystyle f'(c^{+}):=\lim _{h\to 0^{+}}{\frac {f(c+h)-f(c)}{h}}\leq 0,}$$ where the limit exists by assumption, it may be minus infinity.

Similarly, for every h < 0, the inequality turns around because the denominator is now negative and we get $${\displaystyle {\frac {f(c+h)-f(c)}{h}}\geq 0,}$$ hence $${\displaystyle f'(c^{-}):=\lim _{h\to 0^{-}}{\frac {f(c+h)-f(c)}{h}}\geq 0,}$$ where the limit might be plus infinity.

Finally, when the above right- and left-hand limits agree (in particular when f is differentiable), then the derivative of f at c must be zero.

(Alternatively, we can apply Fermat's stationary point theorem directly.)

We can also generalize Rolle's theorem by requiring that f has more points with equal values and greater regularity. Specifically, suppose that

• the function f is n − 1 times continuously differentiable on the closed interval [a, b] and the nth derivative exists on the open interval (a, b), and
• there are n intervals given by a₁ < b₁ ≤ a₂ < b₂ ≤ ⋯ ≤ a_n < b_n in [a, b] such that f (a_k) = f (b_k) for every k from 1 to n.

Then there is a number c in (a, b) such that the nth derivative of f at c is zero.

The requirements concerning the nth derivative of f can be weakened as in the generalization above, giving the corresponding (possibly weaker) assertions for the right- and left-hand limits defined above with f ^{(n − 1)} in place of f.

Particularly, this version of the theorem asserts that if a function differentiable enough times has n roots (so they have the same value, that is 0), then there is an internal point where f ^{(n − 1)} vanishes.

The proof uses mathematical induction. The case n = 1 is simply the standard version of Rolle's theorem. For n > 1, take as the induction hypothesis that the generalization is true for n − 1. We want to prove it for n. Assume the function f satisfies the hypotheses of the theorem. By the standard version of Rolle's theorem, for every integer k from 1 to n, there exists a c_k in the open interval (a_k, b_k) such that f ′(c_k) = 0. Hence, the first derivative satisfies the assumptions on the n − 1 closed intervals [c₁, c₂], …, [c_{n − 1}, c_n]. By the induction hypothesis, there is a c such that the (n − 1)st derivative of f ′ at c is zero.

Rolle's theorem is a property of differentiable functions over the real numbers, which are an ordered field. As such, it does not generalize to other fields, but the following corollary does: if a real polynomial factors (has all of its roots) over the real numbers, then its derivative does as well. One may call this property of a field Rolle's property.^{[citation needed]} More general fields do not always have differentiable functions, but they do always have polynomials, which can be symbolically differentiated. Similarly, more general fields may not have an order, but one has a notion of a root of a polynomial lying in a field.

Thus Rolle's theorem shows that the real numbers have Rolle's property. Any algebraically closed field such as the complex numbers has Rolle's property. However, the rational numbers do not – for example, x³ − x = x(x − 1)(x + 1) factors over the rationals, but its derivative, $${\displaystyle 3x^{2}-1=3\left(x-{\tfrac {1}{\sqrt {3}}}\right)\left(x+{\tfrac {1}{\sqrt {3}}}\right),}$$ does not. The question of which fields satisfy Rolle's property was raised in Kaplansky 1972.^[4] For finite fields, the answer is that only F² and F⁴ have Rolle's property.^[5][6]

For a complex version, see Voorhoeve index.

• Mean value theorem
• Intermediate value theorem
• Linear interpolation
• Gauss–Lucas theorem

• Leithold, Louis (1972). The Calculus, with Analytic Geometry (2nd ed.). New York: Harper & Row. pp. 201–207. ISBN 0-06-043959-9.
• Taylor, Angus E. (1955). Advanced Calculus. Boston: Ginn and Company. pp. 30–37.

• "Rolle theorem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Rolle's and Mean Value Theorems at cut-the-knot.
• Mizar system proof: http://mizar.org/version/current/html/rolle.html#T2

Wikimedia Commons has media related to Rolle's theorem.