Random element
|
Read other articles:

1886 novel by Emilia Pardo Bazán The House of Ulloa Cover of first editionAuthorEmilia Pardo BazánOriginal titleLos pazos de UlloaTranslatorPaul O'Prey and Lucia GravesLanguageSpanishPublished1886PublisherPenguin Books (U.K. first edition)Published in English1990Pages275 (U.K. first edition)ISBN9780140445022 The House of Ulloa (Spanish: Los pazos de Ulloa) is a novel by Emilia Pardo Bazán, published in Spanish in 1886, and translated into English by Paul O'Prey and Lucia Graves, ...

Governor Samuel Johnston presided over the Convention The Fayetteville Convention was a meeting by 271 delegates from North Carolina to ratify the US Constitution. Governor Samuel Johnston presided over the convention, which met in Fayetteville, North Carolina, from November 16 to 23, 1789 to debate on and decide on the ratification of the Constitution, which had recommended to the states by the Philadelphia Convention during the summer of 1787. The delegates ratified the Constitution by a vo...
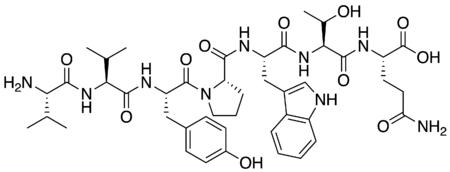
Valorphin Names IUPAC name L-Valyl-L-valyl-L-tyrosyl-L-prolyl-L-tryptophyl-L-threonyl-L-glutamine Identifiers CAS Number 144313-54-2 N[ChemSpider] 3D model (JSmol) Interactive image ChemSpider 27470960 PubChem CID 90470048 InChI InChI=1S/C44H60N8O12/c1-22(2)35(45)40(59)50-36(23(3)4)41(60)49-32(19-25-12-14-27(54)15-13-25)43(62)52-18-8-11-33(52)39(58)48-31(20-26-21-46-29-10-7-6-9-28(26)29)38(57)51-37(24(5)53)42(61)47-30(44(63)64)16-17-34(55)56/h6-7,9-10,12-15,21-24,30-33,35-37,46,...

The history of education in New York City includes schools and schooling from the colonial era to the present. It includes public and private schools, as well as higher education. Annual city spending on public schools quadrupled from $250 million in 1946 to $1.1 billion in 1960. It reached $38 billion in 2022, or $38,000 per public school student.[1] For recent history see Education in New York City. Colonial Further information: Education in the Thirteen Colonies There was limited ...

Outdoor National Hockey League game 2017 NHL Stadium Series 123 Total Philadelphia Flyers 011 2 Pittsburgh Penguins 112 4 DateFebruary 25, 2017VenueHeinz FieldCityPittsburgh, PennsylvaniaAttendance67,318 ← 2016 2018 → The 2017 NHL Stadium Series (officially the 2017 Coors Light NHL Stadium Series for sponsorship reasons) was a regular season National Hockey League (NHL) game played outdoors, part of the Stadium Series of games held at football or baseball stadiums. The P...

Overview of the climate of Sweden Köppen climate classification types of Sweden using the 0°C isotherm Köppen climate classification types of Sweden using the -3°C isotherm The south of Sweden has a temperate climate, despite its northern latitude, with largely four distinct seasons and mild temperatures throughout the year. The winter in the far south is usually weak and is manifested only through some shorter periods with snow and sub-zero temperatures, autumn may well turn into spring ...

Evening meal Part of a series onMeals Meals Suhur Breakfast Second breakfast Elevenses Brunch Lunch Tea Merienda Tiffin Dinner Supper Iftar Siu yeh Snack Combination meal Kids' meal Value meal Components and courses Full-course dinner Tasting menu Amuse-bouche Hors d'oeuvre Soup Entrée Roast Main course Salad Side dish Entremets Dessert Savoury Meal preparation Related concepts À la carte Banquet Buffet Cuisine list Drink Eating Food Grazing History of breakfast Kamayan Table d'hôte Table ...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) قرن: ق�...

Teti convoca Briareo affinché soccorra Zeus dalla ribellione degli altri Olimpi. Calcografia di Tommaso Piroli (1795) da disegno di John Flaxman (1793) Briareo è una figura della mitologia greca, figlio di Urano e Gea. Indice 1 Miti su Briareo 2 Briareo nella cultura 3 Note 4 Bibliografia 5 Altri progetti 6 Collegamenti esterni Miti su Briareo Era uno dei mostri con cinquanta teste e cento braccia, gli Ecatonchiri o Centimani. Esiodo nella Teogonia narra che Poseidone vista la gran forza di...

ماري وزهرة الساحرةメアリと魔女の花 (باليابانية) الشعارملصق الفيلممعلومات عامةالتصنيف فيلم رسوم متحركة الصنف الفني فيلم فنتازيا تاريخ الصدور 8 يوليو 2017[1] (اليابان)19 يناير 2018[2] (الولايات المتحدة)13 سبتمبر 2018[3] (ألمانيا) مدة العرض 102 دقيقة اللغة الأصلية اليابانية مأخو...

Seorang asketis Ājīvika dalam sebuah ukiran Gandhara dari Mahaparinirwana, sekitar abad ke-2 sampai ke-3 Masehi.[1][2][3][4][5] Di kiri: Mahākāśyapa bertemu penganut Ājīvika dan mempelajari parinirwana[6] Ajivika (IAST: Ājīvika) adalah salah satu aliran nāstika atau heterodoks dari filsafat India.[7][8] Diyakini didirikan pada abad ke-5 SM oleh Makkhali Gosala, aliran tersebut adalah sebuah gerakan śramaṇa dan pesain...

У этого термина существуют и другие значения, см. Площадь Тараса Шевченко. Площадь Тараса Шевченкоукр. Площа Тараса Шевченка 50°31′15″ с. ш. 30°26′58″ в. д.HGЯO Общая информация Страна Украина Названа в честьТарас Григорьевич Шевченко Медиафайлы на Викис...

JeanDuc de BerryGambar Jean di dalam manuskrip Très Riches HeuresKelahiran(1340-11-30)30 November 1340Château de VincennesKematian15 Juni 1416(1416-06-15) (umur 75)ParisWangsaValois-BourgogneAyahJean II dari PrancisIbuBonne dari BohemiaPasanganJoan dari ArmagnacJeanne II d'AuvergneAnakJean de Valois, Comte de MontpensierBonne dari BerryMarie, Adipati Wanita Auvergne Jean de Berry (30 November 1340 – 15 June 1416) adalah adalah seorang penguasa yang bergelar Adipati Berry dan Auvergne...

خزانةالنوع أثاث تعديل - تعديل مصدري - تعديل ويكي بياناتخزانة. الخزانة (الجمع: خِزَانَات، خَزَائِن) هي قطعة أثاث منزلية على شكل مربع تحتوي على أدراج مُختلفة لتخزين وحفظ المواد المتنوعة.[1][2][3] وعادةً ما تكون الخزانة مصنوعة من الخشب. وتُسمى الخزانة التي تحتفظ باللب...

Fictional DC Comics superhero Comics character Cosmic BoyCover art for Final Crisis: Legion of Three Worlds #3 (February 2009), art by George Pérez.Publication informationPublisherDC ComicsFirst appearanceAdventure Comics #247 (April 1958)Created byOtto BinderAl PlastinoIn-story informationAlter egoRokk KrinnSpeciesBraalianPlace of originBraalTeam affiliationsLegion of Super-HeroesNotable aliasesPolestar, Time TrapperAbilitiesPowers: Magnetism manipulation Magnetic field / force manipulation...

Semi-permeable paper barrier Filter paper is a semi-permeable paper barrier placed perpendicular to a liquid or air flow. It is used to separate fine solid particles from liquids or gases. Filter paper: used for separating solid from liquid. The raw materials are typically different paper pulps. The pulp may be made from softwood, hardwood, fiber crops, or mineral fibers. Properties Filter paper has various properties. The important parameters are wet strength, porosity, particle retention, v...

Protoattic loutrophoros-amphora by the Analatos Painter, c. 680 BC, Louvre (CA 1960) A loutrophoros (Ancient Greek: λουτροφόρος; Greek etymology: λουτρόν/loutron and φέρω/pherō, English translation: bathwater and carry) is a distinctive type of Greek pottery vessel characterized by an elongated neck with two handles. The loutrophoros was used to carry water for a bride's pre-nuptial ritual bath, and in funeral rituals, and was placed in the tombs of the unmarried.[1...

提示:此条目页的主题不是攝錄。 攝影一名女性用尼康胶片相机拍摄照片型式記錄光或其他電磁輻射 摄影(英語:photography)是指使用某种专门设备进行影像记录的过程。一般我们使用机械照相机或者數碼照相机进行靜態圖片摄影,靜態摄影也会被称为照相[1]。而攝影機(攝像放像機)則可以動態攝影,例如電視、電影。目前部分數位相機、數位攝影機,同�...

「柳州」重定向至此。关于其他用法,请见「柳州 (消歧义)」。 柳州市壯文:Liujcouh柳地级市柳州市风光上起顺时针依次为:柳州柳北区、柳州东门城楼、程阳永济桥、文庙、驾鹤小桃园与驾鹤书院、龙潭公园、柳侯公园与柳侯祠綽號:壶城、桂中商埠柳州市在广西壮族自治区的地理位置坐标:24°19′34″N 109°25′42″E / 24.3262°N 109.4284°E / 24.3262; 10...

Questa voce sugli argomenti giocatori di beach soccer e allenatori di calcio italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Massimiliano EspositoEsposito in azione alla Reggiana nel 1993Nazionalità Italia Altezza174 cm Peso79 kg Calcio RuoloAllenatore (ex attaccante, centrocampista) Termine carriera2012 - giocatore CarrieraSquadre di club1 1990-1993 Catanzaro61 (8)1993-1995 Re...










































