Moment (physics)
|
Read other articles:

No debe confundirse con Estación sencilla Santa Isabel la estación del sistema TransMilenio de Bogotá. Santa Isabel Estación Santa IsabelUbicaciónCoordenadas 33°26′49″S 70°37′50″O / -33.447075, -70.63045Dirección Av. General Bustamante con Avenida Santa IsabelComuna ProvidenciaDatos de la estaciónInauguración 5 de abril de 1997Servicios N.º de andenes 2N.º de vías 2Operador Metro de SantiagoServicios detalladosClasificación Posición SubterráneaColor ...
Ellingen. Ellingen adalah kota yang terletak di distrik Weißenburg-Gunzenhausen di Bavaria, Jerman. Kota Ellingen memiliki luas sebesar 31.25 km² . Ellingen pada tahun 2006, memiliki penduduk sebanyak 3.703 jiwa. lbsKota dan kotamadya di Weissenburg-GunzenhausenAbsberg | Alesheim | Bergen | Burgsalach | Dittenheim | Ellingen | Ettenstatt | Gnotzheim | Gunzenhausen | Haundorf | Heidenheim | Höttingen | Langenaltheim | Mar...

This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (January 2016) (Learn how and when to remove this template message) Graduate School of Media Communications and Performing ArtsAlta Scuola in Media, Comunicazione e SpettacoloOther nameALMEDTypePrivateEstablished2002 ...

Segunda División 2004-2005Liga Adelante 2004-2005 Competizione Segunda División Sport Calcio Edizione 74ª Organizzatore RFEF Date dal 28 agosto 2004al 18 giugno 2005 Luogo Spagna Partecipanti 22 Formula Girone all'italiana Sito web www.lfp.es Risultati Vincitore Cadice Promozioni Cadice Celta Vigo Alavés Retrocessioni Córdoba Terrassa Salamanca UDS Pontevedra Cronologia della competizione 2003-2004 2005-2006 Manuale L'edizione 200...

Demographics of South KoreaPopulation pyramid of South Korea in 2022Population51,430,018 (2023 est.)Growth rate−0.24% (2022 est.)Birth rate4.5 births/1,000 population (2023 est.)Death rate6.9 deaths/1,000 population (2023 est.)Life expectancy82.97 years • male79.88 years • female86.24 years (2022 est.)Fertility rate0.72 children born/woman (2023)[1]Infant mortality rate2.87 deaths/1,000 live birthsNet migration rate2.63 migrant(s)/1,000 population (2022...

American politician & military pilot (born 1966) Martha McSallyOfficial portrait, 2019United States Senatorfrom ArizonaIn officeJanuary 3, 2019 – December 2, 2020Appointed byDoug DuceyPreceded byJon KylSucceeded byMark KellyMember of the U.S. House of Representativesfrom Arizona's 2nd districtIn officeJanuary 3, 2015 – January 3, 2019Preceded byRon BarberSucceeded byAnn Kirkpatrick Personal detailsBornMartha Elizabeth McSally (1966-03-22) March 22, 1966 (...

Tour by the Indian Cricket Team in Sri Lanka during 2021 Indian cricket team in Sri Lanka in 2012 Sri Lanka IndiaDates 21 July – 7 AugustCaptains Mahela JayawardeneAngelo Mathews(5th ODI and Only T20I) MS DhoniOne Day International seriesResults India won the 5-match series 4–1Most runs Kumar Sangakkara (206) Virat Kohli (296)Most wickets Thisara Perera (8)Lasith Malinga (8) Irfan Pathan (8)Player of the series Virat Kohli (Ind)Twenty20 International seriesResults India ...

Bassin de LondresPrésentationType Bassin sédimentaireLocalisationLocalisation Royaume-UniCoordonnées 51° 45′ 50″ N, 0° 26′ 42″ Emodifier - modifier le code - modifier Wikidata Carte géologique du Sud-Est de l’Angleterre et des régions environnant la Manche, montrant le bassin de Londres et ses environs. Le bassin de Londres est un bassin allongé, grossièrement triangulaire d'environ 250 km de long sur lequel se trouve Londres et une ...

Matt PottingerPottinger pada 2011 Wakil Penasehat Keamanan Nasional Amerika SerikatPetahanaMulai menjabat 22 September 2019PresidenDonald TrumpPendahuluCharles KuppermanPenggantiPetahana Informasi pribadiLahir1973/1974 (umur 50–51)Suami/istriYen PottingerAnak2Orang tuaJohn Stanley Pottinger (ayah)PendidikanUniversitas Massachusetts, Amherst (Sarjana)Karier militerPihak Amerika SerikatDinas/cabang Korps Marinir Amerika SerikatMasa dinas2005–2010 (aktif)2010–kini (...

This article is about a shopping centre in Melbourne, Australia. For the railway station, see Melbourne Central railway station. Shopping mall in Victoria, AustraliaMelbourne CentralLocationMelbourne, Victoria, AustraliaCoordinates37°48′37.42″S 144°57′47.32″E / 37.8103944°S 144.9631444°E / -37.8103944; 144.9631444Opening date1991; 33 years ago (1991)[1]DeveloperKumagai GumiManagementGPT GroupOwnerGPT Group[2]ArchitectKisho...

Biblical saint This article is about a figure in the Bible. For other uses, see John Mark (disambiguation). John MarkSt. Mark by Frans Hals, c. 1625Bishop of Byblos[1]DiedFirst century ADVenerated inRoman Catholic Church, Eastern Catholic ChurchesFeastSeptember 27[1] John Mark (Greek: Ἰωάννης Μάρκος, romanized: Iōannēs Markos) is named in the Acts of the Apostles as an assistant accompanying Paul and Barnabas on their missionary journeys. Tradit...

American publicly funded non-profit corporation This article needs to be updated. Please help update this article to reflect recent events or newly available information. (April 2023) Corporation for Public BroadcastingCompany typePrivate, non-profit[1][2]Industry Television Radio FoundedNovember 7, 1967; 56 years ago (1967-11-07)HeadquartersWashington, D.C., U.S.Area servedUnited StatesKey peoplePatricia Harrison (president & CEO)Number of employees100We...

American actor (1887–1966) William FrawleyFrawley in 1951BornWilliam Clement Frawley(1887-02-26)February 26, 1887Burlington, Iowa, U.S.DiedMarch 3, 1966(1966-03-03) (aged 79)Los Angeles, California, U.S.Resting placeSan Fernando Mission CemeteryOther namesBill FrawleyOccupationActorYears active1914–1965Spouse Edna Louise Broedt (m. 1914; div. 1927) William Clement Frawley (February 26, 1887 – March 3, 1966) was an Ameri...
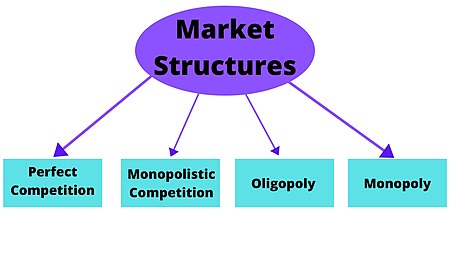
Ability of a firm to raise the market price of a commodity over marginal cost Competition law Basic concepts History of competition law Monopoly and oligopoly Coercive monopoly Natural monopoly Barriers to entry Herfindahl–Hirschman index Market concentration Market power SSNIP test Relevant market Merger control Anti-competitive practices Monopolization Collusion Formation of cartels Price fixing (cases) Bid rigging Tacit collusion Product bundling and tying Refusal to deal Group boycott E...

Fenolftalein Nama Nama IUPAC 3,3-bis(4-hydroxyphenyl)isobenzofuran-1(3H)-one Penanda Nomor CAS 77-09-8 Y Model 3D (JSmol) Gambar interaktif 3DMet {{{3DMet}}} ChEMBL ChEMBL63857 Y ChemSpider 4600 Y DrugBank DB04824 N Nomor EC KEGG D05456 Y PubChem CID 4764 Nomor RTECS {{{value}}} UNII 6QK969R2IF N CompTox Dashboard (EPA) DTXSID0021125 InChI InChI=1S/C20H14O4/c21-15-9-5-13(6-10-15)20(14-7-11-16(22)12-8-14)18-4-2-1-3-17(18)19(23)24-20/h1-12,21-22H YKey: K...

Town in Kota Tinggi, Johor, Malaysia Tanjung Balau Tanjung Balau is a beach town in Kota Tinggi District, Johor, Malaysia. In April 2019, Johor Marine Department detected an oil spill off the coast of Tanjung Balau, covering 4 mautical miles from an estimated 300 tonnes of spilled marine fuel oil.[1] Tourist attractions Tanjung Balau Beach Tanjung Balau Fishermen Museum[2] Wikimedia Commons has media related to Tanjung Balau Beach. References ^ Md Sani, Mohd Sabran (19 April 2...

Genre of music Not to be confused with New wave music. New-ageStylistic originsElectronicambientfolkworldclassicalkrautrockrockeasy listeningminimalprogressive rockCultural origins1960s and early 1970s, Europe and United StatesSubgenres Space music biomusic progressive electronic Neoclassical new-age music Fusion genresCeltic fusionOther topics New Age meditation environmentalism List of new-age music artists vaporwave New-age is a genre of music intended to create artistic inspiration, relax...

1955 South Korean filmPiagolHangul피아골Revised RomanizationPiagolMcCune–ReischauerP'iagol Directed byLee Kang-cheonWritten byKim Chong Hwan (김종환)Produced byKim Byeong-kiStarringKim Jin-kyu Lee Ye-chun (이예춘)CinematographyKang Yeong Hwa (강영화)Edited byYang Ju Nam (양주남)Music byKwak In Geun (곽인건)Release date September 23, 1955 (1955-09-23) Running time110 minutesCountrySouth KoreaLanguageKorean Piagol (Korean: 피아골) is a 1955 South K...

Self-awareness about thinking, higher-order thinking skills Metacognition is an awareness of one's thought processes and an understanding of the patterns behind them. The term comes from the root word meta, meaning beyond, or on top of.[1] Metacognition can take many forms, such as reflecting on one's ways of thinking, and knowing when and how oneself and others use particular strategies for problem-solving.[1][2] There are generally two components of metacognition: (1...

Severo Ochoa nel 1958 Premio Nobel per la medicina 1959 Severo Ochoa de Albornoz (Luarca, 24 settembre 1905 – Madrid, 1º novembre 1993) è stato un biochimico spagnolo naturalizzato statunitense nel 1956. Indice 1 Biografia 2 Carriera 3 Altri progetti 4 Collegamenti esterni Biografia Ochoa è nata a Luarca, Nel 1923 frequentò la Facoltà di Medicina dell'Università di Madrid. Studiò con padre Pedro Arrupe e Juan Negrín fu il suo insegnante. Negrín e Ochoa e un altro studente, e Jo...
































