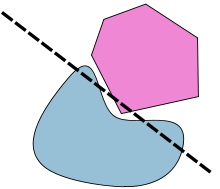
Hyperplane separation theorem
| |||||||||||||||||||||||||||||||||||||
Read other articles:

Psocoptera Periode 299–0 jtyl PreЄ Є O S D C P T J K Pg N Cisuralian – Terkini TaksonomiKerajaanAnimaliaFilumArthropodaKelasInsectaOrdoPsocoptera Shipley, 1904 Subordo Trogiomorpha (7 famili) Troctomorpha (34 famili) Psocomorpha (26 famili) lbs Psocoptera (dalam bahasa Inggris dikenal sebagai booklice, barklice, atau barkflies) adalah sebuah ordo serangga.[1] Mereka muncul pertama kali pada periode Permian, 295 hingga 248 juta tahun silam. Ordo ini sering dianggap sebagai y...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Bandar Udara AketiIATA: noneICAO: FZKNInformasiMelayaniAketi, Democratic Republic of the CongoKetinggian dpl375 mdplPetaFZKNBandar udara di Republik Demokratik KongoLandasan pacu Arah Panjang Permukaan m kaki 950 3.117 Sumber: Great Circle Ma...

Drivetrain transmitting propulsion power For other uses of the word transmission, see Transmission. Gearbox redirects here. For other uses, see Gearbox (disambiguation). Hydraulic automatic transmission (cutaway view)Epicyclic gearing diagram, as used in hydraulic automatic transmissions A transmission (also called a gearbox) is a mechanical device which uses a gear set—two or more gears working together—to change the speed or direction of rotation in a machine.[1][2] Many...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Unitary authority area in England Unitary authority area in EnglandNorth YorkshireUnitary authority areaRipon, the only city in the district and its third-largest settlement.Shown within the ceremonial county of North YorkshireSovereign stateUnited KingdomCountryEnglandRegionYorkshire and the HumberCeremonial countyNorth YorkshireHistoric countyYorkshireUnitary Authority1 April 2023SeatNorthallertonGovernment • TypeUnitary authority • Local AuthorityNorth Yorkshire Cou...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Cet article est une ébauche concernant une localité suédoise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. MantorpLe circuit national de Suède Mantorp Park situé dans la commune.Nom officiel (sv) MantorpGéographiePays SuèdeComté ÖstergötlandCommune suédoise MjölbySuperficie 3,54 km2 (2020)Coordonnées 58° 21′ 13″ N, 15° 17′ 08″ EDémographiePo...

Cet article est une ébauche concernant le basket-ball et la Suisse. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pully Lausanne Basketball Club Généralités Noms précédents Pully Basket, BBC Lausanne Fondation 1951 Couleurs Rouge et Blanc Salle Salle omnisports Arnold-Reymond Salle omnisports de la Vallée de la Jeunesse Siège Pully Championnat actuel Championnat LNB Président Serge Vittoz Entraîneur ...

Group of fruit culttivars This article is about the European plum cultivar. For the species of green plum from Asia, see Prunus mume. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Greengage – news · newspapers · books · scholar · JSTOR (July 2014) (Learn how and when to remove this message) Greengage Scien...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Play based on accounts of mental illness The Manic MonologuesPosterWritten byZachary Burton; Elisa HofmeisterDate premieredMay 2019 (May 2019)Place premieredStanford University, California, USAOriginal languageEnglishSubjectMental Illness The Manic Monologues is a play developed and premiered by Zachary Burton and Elisa Hofmeister at Stanford University.[1][2][3][4][5][6][7][8][9][10] The play consists of aut...

Series of laptops by IBM and Lenovo ThinkPad T seriesT20 – the first in the T seriesDeveloper IBM: 2000–2005 Lenovo: 2005–present Product familyThinkPadTypeNotebook computerRelease dateMay 2000; 24 years ago (2000-05)Operating systemMicrosoft WindowsCPUIntel Core, AMD Ryzen PROPredecessorIBM ThinkPad 600IBM ThinkPad 770Websitehttps://www.lenovo.com/us/en/c/laptops/thinkpad/thinkpadt This article is part of a series on theThinkPad IBM lines: 800 700 600 500 300 A (...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Estonian politician Indrek TarandMEPMember of the European ParliamentIn office1 July 2009 – 30 June 2019ConstituencyEstonia Personal detailsBorn (1964-02-03) 3 February 1964 (age 60)Tallinn, EstoniaPolitical party EstonianIndependent EUEuropean Green PartySpouseKadi TarandChildren3Alma materUniversity of TartuSAIS Bologna, Johns Hopkins University Indrek Tarand (born 3 February 1964) is an Estonian politician and Member of the European Parliament (MEP) from Estonia. ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) بطولة العالم للدراجات على المضمار 1975 التفاصيل التاريخ 1975 الموقع بلجيكا (روكوت) نوع السباق سباق الدراج...

Un treuil est un appareil de levage. C'est un dispositif mécanique permettant de commander l'enroulement et le déroulement d'un câble, d'une chaîne ou de tout autre type de filin destiné à porter ou à tracter une charge. Le treuil est l'une des huit machines simples. Différents types de démultiplication Treuil de carrière à traction animale (restauration d'un ouvrage du XIXe siècle). Treuil de la carrière Auboin de Châtillon (92), association Picar, membre de l'union Rempar...

Jean François GilletNazionalità Belgio Altezza181 cm Peso78 kg Calcio RuoloAllenatore (ex portiere) Squadra Standard Liegi (Portieri) Termine carriera1º luglio 2021 - giocatore CarrieraGiovanili 1989-1996 Standard Liegi Squadre di club1 1996-1999 Standard Liegi4 (-7)1999-2000 Monza37 (-45)2000-2003 Bari76 (-102)2003-2004→ Treviso44 (-48)2004-2011 Bari277 (-306)2011-2012 Bologna29 (-32)2012-2015 Torino49 (-67)2015 Catania16 (-20)2015...

Questa voce sull'argomento allenatori di pallacanestro statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Phog AllenNazionalità Stati Uniti Pallacanestro RuoloAllenatore Termine carriera1956 Hall of fameNaismith Hall of Fame (1959) CarrieraCarriera da allenatore Independence H.S.1905-1908Baker University45-91907-1909 Kansas Jayhawks43-91908-1909Haskell University17-51912-1919&...

1941 film by Budd Boetticher, Rouben Mamoulian Blood and SandTheatrical release posterDirected byRouben MamoulianScreenplay byJo SwerlingBased onthe novelby Vicente Blasco IbanezProduced byAssociate producer:Robert T. KaneProducer:Darryl F. ZanuckStarringTyrone PowerLinda DarnellRita HayworthNazimovaAnthony QuinnJ. Carrol NaishLynn BariJohn CarradineLaird CregarMonty BanksVicente GomezCinematographyErnest Palmer, A.S.C.Ray Rennahan, A.S.C.Edited byRobert BischoffMusic byAlfred NewmanVicente G...

La Chambre des comptes de Savoie était, au cours de la période médiévale, une cour princière spécialisée dans les affaires de finance du comté, puis du duché de Savoie. Le comté de Savoie a été élevé en duché par l'empereur l'empereur Sigismond Ier, le 19 février 1416. Historique Les possessions de la Maison de Savoie vers 1200 Entre le XIIe et le XVe siècle, la Maison de Savoie va agrandir ses possessions qui vont s'étendre du Viennois et du Bugey à l'ouest, au Valais...
















































![{\displaystyle [a_{0},b_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838ee9034d5bf96adfb08ff6cc185c1aee56c18)









![{\displaystyle [a_{0},a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f999eabb0f8a81ac400fc6184c9c4e45c096d406)